 |
Расчет переходных процессов в электрических цепях с некорректной коммутацией
|
|
|
|
Общие принципы расчета переходных процессов в линейных цепях классическим методом. Определение порядка дифференциального уравнения.
1) В индуктивном элементе ток(магнитный поток) после коммутации сохраняет значение, которое он имел до коммутации. iL(0-) = iL(0+).
2) В емкостном элементе напряжение сохраняет в момент коммутации то значение которое оно имело до коммутации. UC(0-) = UC(0+).
3) iL(0+), UC(0+) – начальные условия, если эти величины в момент времени t=-0 были равны 0, то имеют место нулевые начальные условия, а если указанные величины имели какое-то значение, то это не нулевые начальные условия.
4) Расчет ПП классич. методом производится на основе решения дифф. Уравнения цепи составленных по 1 и 2 Законам Кирхгофа.
Порядок дифференциального, следовательно, и характеристического уравнения зависит от числа реактивных элементов приведенной схемы. Главная трудность в решения задачи классическим методом для уравнений высоких порядков состоит в отыскании корней характеристического уравнения и постоянных интегрирования. Поэтому для решения уравнений порядка выше второго применяют другие методы, в частности операторный метод, основанный на применении преобразования Лапласа и исключающий трудоемкую процедуру отыскания постоянных интегрирования.
Для практических целей при анализе переходных процессов в любой схеме классическим методом может быть рекомендован следующий алгоритм.
- Рассчитать принужденный (установившийся) режим при t→∞. Определить принужденные токи и напряжения.
- Рассчитать режим до коммутации. Определить токи в ветвях с индуктивностью и напряжения на конденсаторах. Значения этих величин в момент коммутации является независимыми начальными условиями.
- Составить дифференциальные уравнения для свободного процесса (Е = 0) в схеме после коммутации по законам Кирхгофа или по методу контурных токов. Алгебраизировать данные уравнения, получить характеристическое уравнение и найти его корни. Существуют приемы, упрощающие операцию отыскания корней характеристического уравнения, например, приравнивание нулю входного операторного сопротивления цепи, которое получается путем замены в выражении комплексного сопротивления цепи множителя "jω" на оператор "р".
- Записать общие выражения для искомых напряжений и токов в соответствии с видом корней характеристического уравнения.
- Переписать величины, полученные в п. 4, и производные от них при t = 0.
- Определить необходимые зависимые начальные условия, используя независимые начальные условия.
- Подставив начальные условия в уравнения п. 5, найти постоянные интегрирования.
- Записать законы изменения искомых токов и напряжений.
|
|
|
Классический метод расчета переходных процессов в линейных цепях. Цепи с одним энергоемким элементом
Классический метод расчета переходных процессов в линейных цепях. Цепи с двумя энергоемкими элементами
Расчет переходных процессов в электрических цепях с некорректной коммутацией
К числу задач с некорректными коммутациями относят задачи, в которых нарушаются основные законы коммутации:
uC(0-)=uC(0+); iL(0-)=iL(0+).
Такое название является чисто условным и в целом ряде практически важных задач указанное явление имеет место.
Рассмотрим цепь, представленную на рис. 2.14. Очевидно, что в данной цепи не может выполняться закон непрерывности тока в индуктивности, поскольку i1(0+)=i2(0+)=i(0+), а i1(0-)¹i2(0-)
Дифференциальное уравнение цепи для t ñ 0:
Его решение
(2.10)
Постоянная интегрирования A определяется по начальному значению тока после коммутации i(0+), которое в данном случае мы не можем определить, используя закон коммутации для ветви с индуктивностью, на основании выше сказанного. В нашем случае необходим другой подход. Рассмотрим его.
|
|
|
Дифференциальное уравнение цепи, запишем в виде:
В предположении, что коммутация происходит мгновенно (Dt®0), напряжение на каждой из индуктивностей неограниченно возрастает. При этом сумма 
должна оставаться конечной, т.к. все остальные слагаемые, входящие в уравнение, заведомо конечны.
Каждую из производных din/dt можно представить как предел отношения Din/Dt при Dt®0. Но Di1=i1(0+)-i1(0-) и Di2=i2(0+)-i2(0-). Поэтому:
.
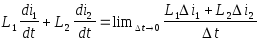Эта сумма остается конечной при Dt®0 только при условии, что
или
.
Последнее равенство выражает закон сохранения магнитного потокосцепления, представляющий обобщение закона коммутации: суммарное магнитное потокосцепление катушек индуктивности в момент коммутации не может измениться скачком.
Используем данный закон для определения i(0+).
До коммутации:
После коммутации:
Следовательно:
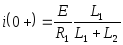
Подставив данное выражение в выражение (2.10), получим
Окончательно:
|
|
|
