Характеристики и параметры элементов нелинейных цепей. Методы расчета установившихся режимов в нелинейных цепях постоянного тока

· Нелинейными называются цепи, в состав которых входит хотя бы один нелинейный элемент.

· Нелинейными называются элементы, параметры которых зависят от величины и (или) направления связанных с этими элементами переменных (напряжения, тока, магнитного потока, заряда, температуры, светового потока и др.). Нелинейные элементы описываются нелинейными характеристиками, которые не имеют строгого аналитического выражения, определяются экспериментально и задаются таблично или графиками.

· Нелинейные элементы можно разделить на двух – и многополюсные. Последние содержат три (различные полупроводниковые и электронные триоды) и более (магнитные усилители, многообмоточные трансформаторы, тетроды, пентоды и др.) полюсов, с помощью которых они подсоединяются к электрической цепи. Характерной особенностью многополюсных элементов является то, что в общем случае их свойства определяются семейством характеристик, представляющих зависимости выходных характеристик от входных переменных и наоборот: входные характеристики строят для ряда фиксированных значений одного из выходных параметров, выходные – для ряда фиксированных значений одного из входных.

· По другому признаку классификации нелинейные элементы можно разделить на инерционные и безынерционные. Инерционными называются элементы, характеристики которых зависят от скорости изменения переменных. Для таких элементов статические характеристики, определяющие зависимость между действующими значениями переменных, отличаются от динамических характеристик, устанавливающих взаимосвязь между мгновенными значениями переменных. Безынерционными называются элементы, характеристики которых не зависят от скорости изменения переменных. Для таких элементов статические и динамические характеристики совпадают.

· Понятия инерционных и безынерционных элементов относительны: элемент может рассматриваться как безынерционный в допустимом (ограниченном сверху) диапазоне частот, при выходе за пределы которого он переходит в разряд инерционных.

· В зависимости от вида характеристик различают нелинейные элементы с симметричными и несимметричными характеристиками. Симметричной называется характеристика, не зависящая от направления определяющих ее величин, т.е. имеющая симметрию относительно начала системы координат: . Для несимметричной характеристики это условие не выполняется, т.е. . Наличие у нелинейного элемента симметричной характеристики позволяет в целом ряде случаев упростить анализ схемы, осуществляя его в пределах одного квадранта.

· По типу характеристики можно также разделить все нелинейные элементы на элементы с однозначной и неоднозначной характеристиками. Однозначной называется характеристика , у которой каждому значению х соответствует единственное значение y и наоборот. В случае неоднозначной характеристики каким-то значениям х может соответствовать два или более значения y или наоборот. У нелинейных резисторов неоднозначность характеристики обычно связана с наличием падающего участка, для которого 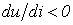, а у нелинейных индуктивных и емкостных элементов – с гистерезисом.

· Наконец, все нелинейные элементы можно разделить на управляемые и неуправляемые. В отличие от неуправляемых управляемые нелинейные элементы (обычно трех- и многополюсники) содержат управляющие каналы, изменяя напряжение, ток, световой поток и др. в которых, изменяют их основные характеристики: вольт-амперную, вебер-амперную или кулон-вольтную.

Расчет НЭЦ постоянного тока применяется:

· Аналитически

· Графически

· Графо-аналитически

· Численный метод

· Итерационный и т.д.

Законы магнитных цепей.

Наименование закона	Аналитическое выражение закона	Формулировка закона
Закон (принцип) непрерывности магнитного потока		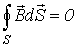Поток вектора магнитной индукции через замкнутую поверхность равен нулю
Закон полного тока		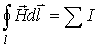Циркуляция вектора напряженности вдоль произвольного контура равна алгебраической сумме токов, охватываемых этим контуром

При анализе магнитных цепей и, в первую очередь, при их синтезе обычно используют следующие допущения:

- магнитная напряженность, соответственно магнитная индукция, во всех точках поперечного сечения магнитопровода одинакова

- потоки рассеяния отсутствуют (магнитный поток через любое сечение неразветвленной части магнитопровода одинаков);

- сечение воздушного зазора равно сечению прилегающих участков магнитопровода.

Это позволяет использовать при расчетах законы Кирхгофа и Ома для магнитных цепей (см. табл. 5), вытекающие из законов, сформулированных в табл. 4.

Таблица 5. Законы Кирхгофа и Ома для магнитных цепей

Наименование закона	Аналитическое выражение закона	Формулировка закона
Первый закон Кирхгофа		Алгебраическая сумма магнитных потоков в узле магнитопровода равна нулю
Второй закон Кирхгофа		Алгебраическая сумма падений магнитного напряжения вдоль замкнутого контура равна алгебраической сумме МДС, действующих в контуре
Закон Ома	где	Падение магнитного напряжения на участке магнитопровода длиной равно произведению магнитного потока и магнитного сопротивления участка