 |
Теория вероятностей и математическая статистика
|
|
|
|
П Р О Г Р А М М А
ГОСУДАРСТВЕННОГО ЭКЗАМЕНА
для выпускников специальности
1-31 03 03 «Прикладная математика»
(срок обучения: 4 года)
Программа утверждена Советом
математического факультета
Протокол № 6
от “ 23 “ января 2017 г.
Декан математического факультета
___________ С.П.ЖОГАЛЬ
Гомель 2017
На государственном экзамене выпускник должен продемонстрировать умение систематизировать информационные сведения программы экзамена, знание основных теорем и понятий, понимание взаимосвязей между ними, умение ими пользоваться.
С учетом этих требований экзаменующийся по каждому вопросу билета должен сделать обзор материала, соответствующего формулировке вопросов, сопровождая ответ доказательством отдельных теорем.
Математический анализ
1. Числа натуральные, рациональные и действительные. Полнота множества действительных чисел.
2. Последовательности и их сходимость (сходящиеся последовательности в метрическом пространстве; сходящиеся последовательности действительных чисел; теорема о существовании предела монотонной ограниченной последовательности). Свойства последовательностей действительных чисел, связанные с арифметическими операциями над последовательностями.
3. Числовые ряды (сходимость числовых рядов; сходимость рядов с неотрицательными членами, признаки их сходимости). Абсолютно сходящиеся ряды, их свойства; условно сходящиеся ряды.
4. Непрерывные функции. Свойства функций, непрерывных на отрезке.
5. Производная функции в точке. Дифференциал. Производные и дифференциалы высших порядков.
6. Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа. Теорема Коши. Формула Тейлора.
|
|
|
7. Локальный экстремум функции одного переменного. Необходимые условия экстремума. Достаточные условия экстремума. Геометрический смысл дифференцируемости и производной функции одного переменного. Касательная, уравнение касательной.
8. Интеграл Римана (определение, существование, свойства).
9. Дифференцируемость интеграла Римана по верхнему пределу. Существование первообразной у непрерывной функции. Формула Ньютона-Лейбница.
10. Дифференцируемость функций нескольких переменных (частные производные и дифференциалы функций многих переменных; необходимые условия дифференцируемости функций многих переменных; достаточные условия дифференцируемости).
11. Производные и дифференциалы высших порядков функции многих переменных. Необходимые и достаточные условия экстремума функции многих переменных.
12. Равномерная сходимость функциональных последовательностей и рядов (критерий Коши равномерной сходимости функциональных последовательностей и рядов; признак Вейерштрасса равномерной сходимости функционального ряда).
13. Двойной интеграл Римана (сведение двойного интеграла к повторному; замена переменных в двойном интеграле; кратные интегралы).
14. Комплексные числа, их геометрическая интерпретация, формула Муавра. Интеграл от функции комплексного переменного. Интегральная теорема Коши и формула Коши.
15. Изолированные особые точки аналитической функции. Вычеты, теорема Коши о вычетах.
Теория вероятностей и математическая статистика
1. Аксиомы теории вероятностей. Классическое определение вероятности. Свойства вероятности.
2. Условная вероятность. Независимость событий. Формулы полной вероятности и Байеса.
3. Схема независимых испытаний Бернулли. Формула Бернулли.
4. Случайная величина. Распределение случайной величины. Функция распределения и её свойства.
|
|
|
5. Дискретные случайные величины. Ряд распределения, функция распределения
6. Абсолютно непрерывные случайные величины. Плотность распределения случайной величины и ее свойства.
7. Математическое ожидание случайных величин и его свойства.
8. Дисперсия случайных величин и ее свойства.
9. Многомерные случайные величины. Функция распределения. Независимость случайных величин.
10. Ковариация и ее свойства. Коэффициент корреляции и его свойства.
11. Выборка, эмпирическая функция распределения, выборочные моменты, гистограмма относительных частот.
12. Точечные оценки, несмещённость, состоятельность, эффективность. Выборочное среднее и выборочная дисперсия, их свойства.
13. Проверка статистических гипотез. Критерии согласия. Критерий согласия Пирсона.
14. Случайный процесс, определение, состояния, реализации случайного процесса. Конечномерные распределения.
15. Классификация случайных процессов: гауссовские случайные процессы, процессы с независимыми приращениями, процессы с некоррелированными приращениями, стационарные процессы, марковские процессы.
16. Цепи Маркова с дискретным временем. Определения цепи Маркова. Переходные вероятности. Уравнения Чепмена-Колмогорова. Начальное распределение. Эргодичность. Стационарное распределение.
Программирование
1. Язык программирования Паскаль. Встроенные типы данных. Операции и выражения.
2. Язык программирования Паскаль. Операторы ввода/вывода. Управляющие операторы.
3. Язык программирования Паскаль. Структурированный тип данных массив. Принцип хранения массивов в оперативной памяти. Типовые алгоритмы обработки массивов.
4. Язык программирования Паскаль. Строковый тип данных. Принцип хранения строк в оперативной памяти. Операции и встроенные функции работы со строками.
5. Язык программирования Паскаль. Назначение типов данных, определяемых пользователем. Синтаксис определения типов, объявления переменных, работы с переменными объявленных типов.
6. Язык программирования Паскаль. Использование функций в языке Паскаль. Способы передачи данных в функции.
7. Язык программирования Паскаль. Использование процедур в языке Паскаль. Способы передачи данных в процедуры.
|
|
|
8. Язык программирования Паскаль. Текстовые, типизированные файлы. Процедуры и функции работы с файлами.
9. Система программирования Delphi. Принципы объектно-ориентированного программирования: инкапсуляция, наследование и полиморфизм.
10. Система программирования Delphi. Составляющие класса: поля, методы, свойства.
11. Система программирования Delphi. Структура проекта. Модули, структура модулей: интерфейсная, исполняемая, инициирующая и завершающая части. Доступ к объявленным в модуле объектам.
12. Система программирования Delphi. Модели баз данных, используемые в Delphi. Архитектуры баз данных в Delphi, технология Data Base Engine (BDE).
13. Система программирования Delphi. Построение приложений баз данных в Delphi. Использование компонента Table. Навигация по набору данных.
14. Система программирования Delphi. Построение приложений баз данных в Delphi. Использование компоненты TQuery. Организация SQL-запросов.
15. Язык программирования C. Основные типы данных и описание переменных в языке С.
16. Язык программирования C. Организация ввода-вывода данных в языке С.
17. Язык программирования C. Операции в языке С. Приоритет операций.
18. Язык программирования C. Операторы управления вычислительным процессом в языке С, примеры их использования.
19. Язык программирования C. Массивы в языке С. Принцип хранения массивов в оперативной памяти. Типовые алгоритмы обработки массивов.
20. Язык программирования C. Указатели в языке С, адресная арифметика. Связь одномерных и двумерных массивов с указателями.
21. Язык программирования C. Работа с динамической памятью. Динамическое выделение памяти для одномерных и двумерных массивов.
22. Язык программирования C. Функции в языке С. Способы передачи информации между функциями.
23. Язык программирования C. Типы данных языка С, определяемые пользователем: перечисления, структуры, объединения. Оператор typedef.
24. Язык программирования C. Классы памяти, область действия, область видимости, время жизни переменных.
|
|
|
25. Язык программирования C. Функции с переменным количеством аргументов. Передача параметров в функцию main().
26. Язык программирования C++. Понятие и описание классов в языке С++.
27. Язык программирования C++. Доступ к полям класса и вызов методов класса в языке С++.
28. Язык программирования C++. Конструкторы и деструктор класса в языке С++, специальные конструкторы.
29. Язык программирования C++. Наследование классов в языке С++, базовый и производный классы.
30. Язык программирования C++. Полиморфизм и виртуальные функции в языке С++.
ЛИТЕРАТУРА
Математический анализ
1. Кудрявцев Л.Д. Курс математического анализа (в двух томах). – М.: Высшая школа, 1991.
2. Демидович Б.П. Сборник задач и упражнений по математическому анализу. – М.: Наука, 1997.
3. Лабораторный практикум по математическому анализу: Учебное пособие / Бруй И.Н., Гаврилюк А.В., Ермаков В.Г. и др. – Мн.: Вышэйшая школа, 1991.
4. Привалов И.И. Введение в теорию функций комплексного переменного. – М., 1984.
5. Сидоров Ю.В., Федорюк М.В., Шабунин М.И. Лекции по теории функций комплексного переменного. – М.: Наука, 1989.
6. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. – М.: Наука, 1987.
7. Смирнов В.И. Курс высшей математики. Т.1-5. – М., 1974-1979.
8. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч.1, ч.2. – М.: Наука, 1980, 1982.
Теория вероятностей и математическая статистика
1. Малинковский, Ю.В. Теория вероятностей и математическая статистика (часть 1. Теория вероятностей): Учебное пособие / Ю.В. Малинковский. – Гомель: УО «ГГУ им.Ф.Скорины», 2004. – 355 с.
2. Малинковский, Ю.В. Теория вероятностей и математическая статистика (часть 2. Математическая статистика): Учебное пособие / Ю.В. Малинковский. – Гомель: УО «ГГУ им.Ф.Скорины», 2004. – 146 с.
3. Севастьянов, Б.А. Курс теории вероятностей и математической статистики / Б.А. Севастьянов. – М.: Наука, 1980. – 256 с.
4. Ширяев, А.Н. Вероятность / А.Н. Ширяев. – М., 1980. – 576 с.
5. Севастьянов, Б.А. Сборник задач по теории вероятностей / Б.А. Севастьянов, В.П. Чистяков, А.М. Зубков. – М.: Наука, 1980. – 276 с.
6. Прохоров, А.В. Задачи по теории вероятностей / А.В. Прохоров, В.Г. Ушаков, Н.Г. Ушаков. – М.: Наука, – 1986. – 328 с.
7. Крамер, Г. Математические методы статистики. – М.: Мир, 1975. – 464 с.
8. Боровков, А.А. Курс теории вероятностей / А.А. Боровков. – М.: Наука, 1976. – 432 с.
9. Ширяев, А.Н. Вероятность / А.Н. Ширяев. – М., 1980. – 576 с.
Программирование
1. Долинский, М.С. Алгоритмизация и программирование на Turbo Pascal от простых до олимпиадных задач / М.С. Долинский. – СПб: Питер, 2005. – 237с.
|
|
|
2. Вальвачев, А. Н. Программирование на языке Delphi. Учебное пособие. / А. Н. Вальвачев, К. А. Сурков, Д. А. Сурков, Ю. М. Четырько. – 2005.
3. Касьянов, В.Н. Сборник заданий по практикуму на ЭВМ / В.Н. Касьянов, В.К. М. Сабельфельд, – М.: Наука, 1986. – 272с.
4. Долинский, М.С. Решение сложных и олимпиадных задач по программированию: Учебное пособие / М.С. Долинский. – СПб: Питер, 2006. – 366с.
5. Златопольский, Д. М. Сборник задач по программированию / Д. М. Златопольский. – СПб.: БХВ-Петербург, 2007.
6. Долинский, М.С. Конспект опорных схем лекций. (распространяется на магнитных носителях).
7. Котов, В. М. Структуры данных и алгоритмы. Теория и практика: учеб. пособие / В. М. Котов, Е. П. Соболевская. – Минск: БГУ, 2004.
8. Вальвачев, А.Н. Программирование на языке Паскаль для персональных ЭВМ ЕС: справ. пособие / А.Н. Вальвачев, В.С. Крисевич – Мн.: Выш. шк., 1989. – 223 с.
9. Уилсон С. Принципы проектирования и разработки программного обеспечения. Учебный курс. – СПб, 2003.
10. Фаронов, В. В. Турбо Паскаль 7.0. Учебный курс / В. В. Фаронов. – М.: Кнорус, 2011.
11. Фаронов, В. В. Турбо Паскаль 7.0. Практика программирования / В. В. Фаронов. – М.: Кнорус, 2009.
12. Бобровский, С. И. Delphi7: учебный курс / С. И. Бобровский. – СПб.: Питер, 2008. – 736 с.
13. Зубов, А. Программирование на Delphi. Трюки и эффекты / А. Зубов. – СПб.: Питер, 2005. – 396 с.
14. Культин, Н. Б. Основы программирования в Delphi7 / Н. Б. Культин. – СПб.: БХВ-Петербург, 2003. – 638 с.
15. Стивенс, Р. Delphi. Готовые алгоритмы / Р. Стивенс; пер. с англ. Мерещука П.А. – 2-е изд. стер. – М.: ДМК Пресс; СПб.: Питер, 2004. – 384с.
16. Сурков, К. Программирование в среде Delphi 2.0 / К. Сурков, Д. Сурков, А. Вальвачев. – Мн.: ООО «Попурри», 1997. – 640 с.
17. Сухарев, М. В. Основы Delphi. Профессиональный подход / М. В. Сухарев. – СПб.: Наука и техника, 2004. – 614 с.
18. Фаронов, В. В. Delphi. Программирование на языке высокого уровня / В. В. Фаронов. – СПб.: Питер, 2007.
19. Вирт, Н. Алгоритмы и структуры данных / Н. Вирт. – СПб.: Невский Диалект, 2001.
20. Голицына, О. Л. Основы алгоритмизации и программирования: учеб. пособие / О. Л. Голицына, И. И. Попов. – М.: ФОРУМ, 2008.
21. Сурков, Д.А. Программирование в среде Borland Pascal для Windows: справочное пособие /Д.А. Сурков и др – Мн.: Выс. шк., 1996.
22. Керниган, Б. Язык программирования C / Б. Керниган, Д. Ритчи. – М.: Вильямс, 2013. – 304 с.
23. Шилд, Г. Полный справочник по С / Г. Шилд. – М.: Вильямс, 2009. – 704 с.
24. Прата, С. Язык программирования С. Лекции и упражнения / С. Прата. – М.: Вильямс, 2013. – 960 с.
25. Павловская, Т. К. С/С++. Программирование на языке высокого уровня / Т. К. Павловская. – СПб.: Питер, 2013. – 464 с.
26. Шилд, Г. C++. Базовый курс / Г. Шилд. – М.: Вильямс, 2012. – 624 с.
27. Страуструп, Б. Язык программирования С++. Специальное издание / Б. Страуструп. – М.: Бином, 2012. – 1136 с.
28. Лафоре, Р. Объектно-ориентированное программирование в С++ / Р. Лафоре. – СПб.: Питер, 2011. – 928 с.
29. Немнюгин, С.А. Turbo Pascal: практикум / С.А. Немнюгин. – СПб.: Питер, 2000. – 256 с.
30. Фаронов, В.В. Turbo Pascal 7.0. Начальный курс: учебное пособие / В.В. Фаронов. – М.: «Нолидж», 1997. – 616 с.
31. Фаронов, В.В. Turbo Pascal 7.0. Практика программирования: учебное пособие / В.В. Фаронов. – М.: «Нолидж», 2001. – 416 с.
32. Турбо Паскаль 7.0. – К.: Торгово-издательское бюро BHV, 1996. – 448с.
33. Фаронов, В.В. Delphi 5. Учебный курс / В.В. Фаронов – М.: «Нолидж», 2000. – 608 с.
34. Фаронов, В.В. Программирование баз данных в Delphi 7. Учебный курс / В.В. Фаронов. – Спб.: Питер, 2006. – 459 с.
35. Керниган, Б. Язык программирования С. 3-е изд.: пер. с англ. / Б. Керниган, Д. Ритчи. – СПб.: Невский диалект, 2001.
36. Павловская, Т.А. С/С++. Программирование на языке высокого уровня / Т.А. Павловская. – СПб.: Питер, 2002.
37. Прата, С. Язык программирования С: лекции и упражнения. 5-е изд.: пер. с англ. / С. Прата. – М.: Издательский дом «Вильямс», 2013.
38. Страуструп, Б. Язык программирования С++. 3-е изд.: пер. с англ. / Б. Страуструп. – СПб.: М.: Невский Диалект – изд. БИНОМ, 1999.
39. Шилдт, Г. Самоучитель С++: Пер. с англ. / Г. Шилдт. – Санкт-Петербург: ВНV-Санкт-Петербург, 1998.
ПЕРЕЧЕНЬ ЗАДАЧ
Математический анализ
1. Найти пределы 
; 
.
2. Является ли функция 
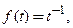
непрерывной на 
? Дифференцируемой на ? Найти ее производную в тех точках, где она существует.
3. Проведя исследование, построить график функции 
.
4. Вычислить следующий интеграл: 
.
5. Найти 
где 
6. Вычислить 
.
7. Найти площадь фигуры, ограниченной кривыми y = 2 x - x 2, x + y = 0.
8. Найти: 
.
9. Исследовать на сходимость 
.
10. Исследовать ряд на сходимость
.
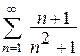11. Исследовать на сходимость 
.
12. Написать ряд Фурье функции 
на отрезке 
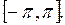
13. Найти области сходимости функционального ряда и его сумму. Исследовать сумму ряда на непрерывность
14. Найти 
, если 
15. Найти дифференциал d2u, если u = x 3 + y 3 + xy (x - y)
16. Изменить порядок интегрирования в следующем повторном интеграле
17. Вычислить 
, где точка О имеет координаты (0;0), а точка А – координаты (1;1), по следующим кривым:
а) ОА - отрезок прямой линии;
б) ОА - парабола, ось которой есть OY;
в) ОА - ломаная линия, состоящая из отрезка ОВ, оси ОХ и отрезка ВА, параллельного оси OY.
18. Применяя формулу Грина, вычислить следующий криволинейный интеграл:
, где 
- окружность с уравнением x 2 + y 2 = 4.
19. Вычислить предел: 
.
20. Существуют ли такие a и b, при которых функция
всюду непрерывна? Всюду дифференцируема?
21. Вычислить интеграл: 
.
22. Вычислить интеграл: 
.
23. Вычислить двойной интеграл 
, где область 
ограничена кривыми 
24. Вычислить двойной интеграл 
где область ограничена линиями 
25. Вычислить двойной интеграл 
где область есть круг с границей 
.
26. Найти изолированные особые точки функции
и выяснить их характер.
27. Найдите все значения суммы 
.
28. Вычислите вычет 
.
29. Вычислите вычет 
.
30. Вычислите интеграл 
.
|
|
|
