 |
Теория вероятностей и математическая статистика
|
|
|
|
1. В ящике имеется 6 деталей, среди которых 2 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятности того, что среди извлеченных деталей ровно одна окрашена.
2. В первой урне 2 белых и 3 черных шара, во второй 4 белых и 5 черных шаров. Из первой урны взяли 2 шара, из второй 3 шара. Найти вероятность, что все вынутые шары одного цвета.
3. Студент знает ответы на 40 вопросов из 76. Найти вероятность того, что на экзамене он сможет ответить на оба вопроса из вытянутого им наудачу билета.
4. В ящике 10 красных и 6 синих пуговиц. Наудачу извлекают три пуговицы. Найти вероятность того, что они будут синего цвета.
5. Ребёнок играет с 10 буквами разрезной азбуки А, А, А, Е, И, К, М, М, Т, Т. Какова вероятность того, что при случайном расположении букв в ряд он получит слово «математика»?
6. На отрезок АВ длины 5 наудачу брошено четыре точек. Найти вероятность того, три точки будут находиться от точки А на расстоянии, меньшем 2, а одна – на расстоянии, большем 2.
7. На отрезке длины 6 наудачу выбирают две точки. Найти вероятность того, что сумма расстояний от этих точек до правого конца отрезка превзойдет 2.
8. Игральная кость подбрасывается три раза. Случайная величина ξ – количество выпадений тройки. Найти ряд распределения и функцию распределения случайной величины 
.
9. Случайная величина задана рядом распределения
Найти математическое ожидание и дисперсию этой случайной величины.
10. Плотность распределения непрерывной случайной величины 
в интервале (0,2) равна f (x)=0,5; вне этого интервала 0. Найти математическое ожидание и дисперсию случайной величины .
11. Задана плотность распределения вероятностей случайной величины :
|
|
|
.
Найти постоянный параметр 
, математическое ожидание случайной величины 
.
12. В результате наблюдений случайной величины 
получена выборка: 3,4,2,1,1,2,2,2,4,1,2,3,1,1,2,2,1,2,1,3. Найти выборочное среднее, несмещенную выборочную дисперсию.
13. Пусть 
, методом моментов найти оценку параметров 
и 
.
14. Пусть 4,3,1,2,2,1,2,2,4,1,2,3,1,1,2,2,1,2,3,1 – выборка из нормального распределения 
. Найти несмещенную оценку 
, несмещенную оценку 
.
15. Пусть 
– случайная величина, имеющая показательное распределение с параметром 5, 
, 
. Построить реализации случайного процесса 
. Найти конечномерные распределения.
16. Найти стационарное распределение процесса размножения и гибели с пространством состояний 
, заданного интенсивностями:
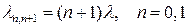
17. В урне три белых и семь черных шаров. Какова вероятность того, что среди вынутых наугад трех шаров окажутся три черных.
18. В партии из 10 деталей имеется 8 стандартных. Наудачу выбраны 4 детали. Найти вероятность того, что все извлеченные детали будут стандартными.
19. В группе 12 студентов, среди которых 8 успевающих. Наудачу выбрали 9 студентов. Какова вероятность того, что среди отобранных студентов 5 успевающих?
20. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
21. Вероятность попадания в цель первым стрелком 0,6, а вторым стрелком 0,8. Стрелки выстрелили одновременно. Какова вероятность того, что хотя бы один из них попадет в цель?
22. Студент пришел на экзамен, зная лишь 20 из 25 вопросов программы. Экзаменатор задал студенту 3 вопроса. Найти вероятность того, что студент знает все эти вопросы.
23. Всхожесть семян данного сорта растений оценивается с вероятностью, равной 0,8. Какова вероятность того, что из трех посеянных семян взойдут не менее двух?
24. Игральная кость бросается 6 раз. Найти вероятность того, что все 6 раз выпадет разное число очков.
|
|
|
25. Из отрезка [0;2] наудачу выбирают две точки. Найти вероятность того, что сумма координат этих точек превзойдет 1.
26. На отрезке длины 5 наудачу выбирают две точки. Найти вероятность того, что сумма расстояний от этих точек до начала отрезка не превзойдет длины отрезка.
27. Бросают три монеты. Случайная величина 
– число выпавших «гербов»; Построить ряд распределения, функцию распределения 
случайной величины.
28. Из урны с 5 белыми и 25 чёрными шарами извлекли один шар. Случайная величина – число вынутых белых шаров. Построить ряд распределения случайной величины, найти математическое ожидание и дисперсию.
29. Вероятность попадания мячом в корзину равна 0,3. Случайная величина ξ – количество попаданий при двух бросках. Построить ряд распределения случайной величины ξ; найти математическое ожидание.
30. Плотность распределения непрерывной случайной величины ξ в интервале (1,3) равна f(x)= 
; вне этого интервала 0. Найти постоянный параметр С, математическое ожидание случайной величины.
31. В результате наблюдений случайной величины получена выборка:
2, 2, 2, 1, 3, 2, 2, 2, 4, 1, 4, 3, 1, 1, 2, 2, 1, 3, 1, 1. Найти выборочное среднее, несмещенную выборочную дисперсию.
|
|
|
