Понятие системы счисления. Позиционные и непозиционные системы счисления

Лекция №1 по теме «Системы счисления»

Системой счисления называется способ записи чисел с помощью определенных символов.

B любой системе счисления для представления чисел выбираются некоторые символы, называемые базисными числами, а все остальные числа получаются в результате каких-либо операций из базисных чисел. Символы, используемые для записи чисел, могут быть любыми, только они должны быть разными и значение каждого из них должно быть известно. B современном мире наиболее распространенным является представление чисел посредством арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Системы счисления различаются выбором базисных чисел и правилами образования из них остальных чисел.

Все системы счисления можно разделить на два класса: позиционные и непозиционные.

Система счисления называется позиционной, если зна­чение каждой цифры (её вес) изменяется в зависимости от ее положения (т.е. позиции) в последовательности цифр, изображаю­щих число. В непозиционной системе счисления вес цифры не зависит от ее положения в изображении числа.

Наиболее известным примером непозиционной системы является римская система счисления.

В римской системе счисления базисными являются числа 1, 5, 10, 50, 100, 500, 1000, которые обозначаются знаками, соответственно I, V, X, L, C, D, M, а другие числа получаются путем сложения и вычитания базисных:

1) если цифра справа меньше или равна цифре слева, то эти цифры складываются;

2) если цифра слева меньше, чем цифра справа, то левая цифра вычитается из правой.

B римской системе счисления каждый числовой знак в записи любого числа имеет одно и то же значение, т.е. значение числового знака не зависит от его расположения и записи числа. Таким образом, римская система счисления не является позиционной.

Так, например, число 146 в римской системе счисления имеет вид: CXLVI (С –100, XL – 40, VI – 6). Здесь число 40 получается посредством вычитания из 50 числа 10, а 6 – посредством сложения чисел 5 и 1.

Недостатком непозиционных систем счисления, из-за которых они представляют лишь исторический интерес, является отсутствие формальных правил записи чисел и, соответственно, арифметических действий над ними (хотя по традиции римскими числами часто пользуются при нумерации глав в книгах, веков в истории и др.).

Для изображения (или представления) чисел в настоящее время используются в основном позиционные системы счис­ления. Привычной для всех является десятичная система счис­ления. B этой системе для записи любых чисел используется только десять разных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Эти цифры введены для обозначения первых десяти последовательных чисел, а следующие числа (начиная с 10) обозна­чаются уже без использования новых цифр. Тем са­мым сделан важный шаг в построении системы счисления: зна­чение каждой цифры поставлено в зависимость от того места, где она стоит в изображении числа.

Десятичная система счисления основана на том, что десять единиц каждого разряда объединяются в одну единицу соседнего старшего разряда. Таким образом, каждый разряд имеет вес, равный степени 10.

Например, в записи числа 535.25 цифра 5 повторена три раза, при этом самая левая цифра 5 означает количество сотен (ее вес равен 10²); цифра 5, стоящая перед точкой, означает количество единиц (ее вес равен 10⁰), a самая правая цифра 5 (после точки) – количество сотых долей единицы (ее вес равен 10^-2), так что последова­тельность цифр 535.25 представляет собой сокращенную за­пись выражения:

.

Десятичная запись любого числа 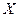в виде последовательности цифр:

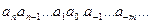(1)

основана на представлении этого числа в виде полинома:

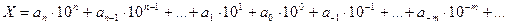, (2)

где каждый коэффициент может быть одним из базисных чисел.

Запись числа 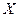в виде (1) представляет собой просто перечисление всех коэффициентов этого полинома. Точка, отделяющая целую часть числа от дробной, служит для фиксации конкретных значений каждой позиции в этой последовательности цифр и является началом отсчета.

Число единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называется основанием позиционной системы счисления, а сама система счисления называется -ичной. Например, основанием десятичной системы счисления является число 10; двоичной – число 2; троичной – число 3, восьмеричной – число 8 и т.д. Другими словами, основание системы счисления – это количество используемых цифр для записи чисел в данной системе счисления.

Для записи произвольного числа в -ичной системе счисления достаточно иметь разных цифр. Обычно в качестве базисных чисел берутся последовательные целые числа от 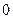до 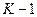включительно. Например, в троичной системе счисления любое число может быть выражено посредством цифр 0, 1, 2; в четверичной – 0, 1, 2, 3; в восьмеричной – 0, 1, 2, 3, 4, 5, 6, 7.

Числа можно записать как суммы степеней не только числа 10, но и любого другого натурального числа, большего единицы. Например, в Древнем Вавилоне использовалась система счисления с основанием 60. Деление часа на 60 минут, а минуты – на 60 секунд заимствовано именно из этой системы счисления. A то, что человечество выбрало в качестве основания системы счисления число 10, вероятно, связано с тем, что природа наделила людей десятью пальцами.

Запись произвольного числа 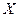в -ичной позиционной системе счисления основывается на представлении этого числа в виде полинома:

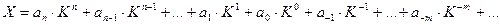, (3)

где каждый коэффициент может быть одним из базисных чисел и изображается одной цифрой.

Формула (3) используется для перевода чисел из -ичной системы счисления в десятичную.

Как и в десятичной системе счисления, число 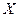, представленное в -ичной системе счисления, можно кратко записать в виде (1) путем перечисления всех коэффициентов полинома (3) с указанием позиционной точки. Последовательность цифр, представленная формулой (1), является изображением числа 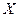в -ичной системе счисления.

Арифметические действия над числами в любой позиционной системе счисления производятся по тем же принципам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими полиномами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые имеют место при данном основании системы счисления.

Для указания того, в какой системе счисления записано число, условимся при его изображении основание системы счисления указывать в виде нижнего индекса при нем, например: 254.21₈ (для чисел в десятичной системе счисления этот индекс можно не использовать).

 

12	Поделиться:

Воспользуйтесь поиском по сайту: