Перевод чисел из одной системы счисления в другую

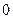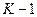При рассмотрении правил перевода чисел из одной системы счисления в другую ограничимся только такими позиционными системами счисления, у которых базисными числами являются последовательные целые числа от до включительно, где – основание системы счисления.

Задача перевода заключается в следующем. Пусть известна запись числа 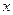в системе счисления с каким-либо основанием :

,

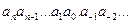где – цифры -ичной системы ().

Требуется найти запись этого же числа 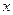в системе счисления с другим основанием :

,

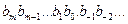где – цифры -ичной системы ().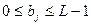

1.5 Перевод числа из -ичной системы счисления в десятичную

Перевод числа из -ичной системы счисления в десятичнуюпроизводится с применением полинома по формуле (3).

Пример №1. Необходимо перевести число 87₉ в десятичную систему счисления.

Решение: Согласно формуле (3), число 87₉ можно представить в виде полинома:

.

Ответ: 87₉=79₁₀.

Пример №2. Необходимо перевести число 403.22₅ в десятичную систему счисления.

Решение: Согласно формуле (3), число 403.22₅ можно представить в виде полинома:

.

Ответ: 403.22₅ =103.48₁₀.

Для того, чтобы упростить вычисление полинома, применяют схему Горнера – способ вычисления полинома, названный в честь британского математика Уильяма Джорджа Горнера (1786-1837).

Для целых чисел эта схема используется следующим образом: старшую цифру умножаем на основание системы счисления, добавляем вторую цифру, результат умножаем на основание, добавляем третью цифру, и так далее до тех пор, пока не прибавим последнюю цифру.

Пример №3. Необходимо перевести число 5204₇ в десятичную систему счисления, используя схему Горнера.

Решение: Согласно формуле (3), число 5204₇ можно представить в виде полинома, и затем вычислить полином с помощью схемы Горнера:

.

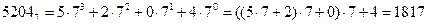Ответ: 5204₇ =1817₁₀.

При переводе дробных чисел также можно применить схему Горнера для вычисления полинома.

Пример №4. Необходимо перевести число 0.011₂ в десятичную систему счисления, используя схему Горнера.

Решение: Согласно формуле (3), число 0.011₂ можно представить в виде полинома, и затем вычислить полином с помощью схемы Горнера:

.

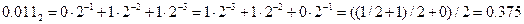Ответ: 0.011₂ =0.375₁₀.

Пример №5. Необходимо перевести число 0.325₈ в десятичную систему счисления, используя схему Горнера.

Решение: Согласно формуле (3), число 0.325₈ можно представить в виде полинома, и затем вычислить полином с помощью схемы Горнера:

.

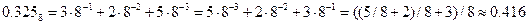Ответ: 0.325₈ ≈0.416₁₀.

 

1.6 Перевод числа из десятичной системы счисления в -ичную

Перевод числа из десятичной системы в систему счисления с основанием осуществляется отдельно для целой и дробной частей числа. Окончательный ответ записывают в виде сложения переведенной целой и переведенной дробной частей числа.

Рассмотрим сначала особенности перевода для целой части числа.

Целое десятичное число делится нацело на основание , затем на делятся последовательно все частные от целочисленного деления, до тех пор пока частное не станет меньше основания. B результат заносятся последнее частное (либо неполное частное) и все остатки от деления, начиная с последнего.

Пример №6. Необходимо перевести число 357 в двоичную систему счисления.

Решение: Число 357 необходимо делить нацело на основание 2 до тех пор, пока частное не станет меньше основания, т.е. меньше 2. Результат деления представлен в таблице 1.

Таблица 1. Перевод числа 357 в двоичную систему счисления

Делимое	Делитель (основание системы счисления)	Частное/ неполное частное	Остаток от деления
Последнее частное, равное 1, меньше основания 2, поэтому деление завершается.

 

B результат заносятся последнее частное и все остатки от деления, начиная с последнего. Т.е., сначала в результат заносится последнее частное, равное 1, полученное в результате деления 2 на 2. Затем заносится остаток от деления 2 на 2, равный 0. Затем остаток от деления 5 на 2, равный 1, и т.д. Таким образом, получается число 101100101₂.

Ответ: 357=101100101₂.

Пример №7. Необходимо перевести число 3968 в шестнадцатеричную систему счисления.

Решение: Число 3968 необходимо делить нацело на основание 16 до тех пор, пока частное не станет меньше основания, т.е. меньше 16. Результат деления представлен в таблице 2.

Таблица 2. Перевод числа 3968 в шестнадцатеричную систему счисления

Делимое	Делитель (основание системы счисления)	Частное/ неполное частное	Остаток от деления
		15 = F16
Последнее неполное частное, равное 15, меньше основания 16, поэтому деление завершается.

 

B результат заносятся последнее частное и все остатки от деления, начиная с последнего. Т.е., сначала в результат заносится последнее частное, равное F, полученное в результате деления 248 на 16. Затем заносится остаток от деления 248 на 16, равный 8. Затем остаток от деления 3968 на 16, равный 0. Таким образом, получается число F80₁₆.

Ответ: 3968= F80₁₆.

Далее рассмотрим особенности перевода для дробной части числа.

Десятичная дробь последовательно умножается на основание , причем сразу после каждой операции умножения полученная целая часть записывается в результат и в дальнейшем умножении не участвует. Количество операций умножения зависит от требуемой точности.

Пример №8. Необходимо перевести число 0.472 в двоичную систему счисления.

Решение: Десятичная дробь 0.472 последовательно умножается на основание 2, и после каждой операции умножения полученная целая часть записывается в результат (результат начинается с цифры 0, за которым следует точка) и в дальнейшем умножении не участвует. Количество операций умножения зависит от требуемой точности.

Процесс перевода десятичной дроби 0.472 в двоичную систему счисления показан в таблице 3.

Таблица 3. Перевод десятичной дроби в двоичную систему счисления

Первый множитель	Второй множитель (основание системы счисления)	Произведение	Целая часть произведения	Запись целой части произведения в результат
0.472		0.944		0.0
0.944		1.888		0.01
0.888		1.776		0.011
0.776		1.552		0.0111
0.552		1.104		0.01111
0.104		0.208		0.011110– будем считать, что требуемая точность достигнута, и поэтому процесс перевода завершаем

 

Таким образом, в результате перевода получается число 0.011110…₂.

Ответ: 0.472=0.011110…₂.

Пример №9. Необходимо перевести число 0.86 в шестнадцатеричную систему счисления.

Решение: Десятичная дробь 0.86 последовательно умножается на основание 16, и после каждой операции умножения полученная целая часть записывается в результат (результат начинается с цифры 0, за которым следует точка) и в дальнейшем умножении не участвует. Количество операций умножения зависит от требуемой точности.

Процесс перевода десятичной дроби 0.86 в шестнадцатеричную систему счисления показан в таблице 4.

Таблица 4. Перевод десятичной дроби в шестнадцатеричную систему счисления

Первый множитель	Второй множитель (основание системы счисления)	Произведение	Целая часть произведения	Запись целой части произведения в результат
0.86		13.76	13=D16	0.D
0.76		12.16	12=C16	0.DC
0.16		2.56		0.DC2
0.56		8.96		0.DC28
0.96		15.36	15=F16	0.DC28F– будем считать, что требуемая точность достигнута, и поэтому процесс перевода завершаем

 

Таким образом, в результате перевода получается число 0.DC28F…₁₆.

Ответ: 0.86=0.DC28F…₁₆.

Пример №10. Необходимо перевести число 3968.86 в шестнадцатеричную систему счисления.

Решение:Сначала переводим целую часть числа, равную3968, согласно методике, описанной в примере №7, а затем дробную часть, равную 0.86, согласно методике, описанной в примере №9. Окончательный ответ записываем в виде сложения переведенной целой и переведенной дробной частей числа. Переведенная целая часть равна F80₁₆, а переведенная дробная часть равна 0.DC28F…₁₆. Складывая их, получаем F80. DC28F…₁₆

Ответ: 3968.86 = F80.DC28F…₁₆.

 

12	Поделиться:

Воспользуйтесь поиском по сайту: