 |
Виды гидродинамического несовершенства скважин, методики определения коэффициента гидродинамического совершенства.
|
|
|
|
Мордвинов А.А. Освоение эксплуатационных скважин, 2008-с.99
1 ОЦЕНКА ГИДРОДИНАМИЧЕСКОГО СОВЕРШЕНСТВА СКВАЖИН
4.1. Понятие о гидродинамическом совершенстве скважин
В промысловой практике для эффективного планирования и регулирования процесса разработки месторождений необходимо знать потенциальные добывные возможности каждой скважины.
Известно, что установившийся приток несжимаемой ньютоновской жидкости в гидродинамически совершенную скважину часто описывается формулой Дюпюи:
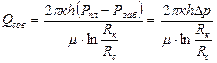, (4.1)
где: Qсов — величина притока в пластовых условиях в гидродинамически совершенную скважину, м3/с;
к — коэффициент проницаемости пласта в зоне дренирования (проницаемость пласта), м2;
h — эффективная нефтенасыщенная толщина пласта, м;
Рпл — давление в пласте на контуре питания скважины (пластовое давление), Па;
Рзаб — давление в скважине в интервале продуктивного пласта (забойное давление), Па;
∆р — величина перепада давления, за счет которого пластовая жидкость движется к забою скважины (депрессия на пласт), Па;
µ — коэффициент динамической вязкости жидкости, Па*с;
Rк — радиус кругового контура питания скважины, м;
Rс — радиус скважины по долоту, м.
Эта формула справедлива для установившегося плоскорадиального притока несжимаемой капельной жидкости к одиночной скважине, расположенной в центре кругового пласта радиусом Rк, дренирующей открытым забоем однородный пласт по всей его толщине.
Важно отметить, что при логарифмическом распределении давления в дренируемом пласте вокруг работающей скважины основная доля перепада давления приходится на зону пласта, примыкающую к забою скважины. Так, например, если приток осуществляется от контура питания, находящегося на расстоянии 300 метров, до стенки скважины радиусом 10 сантиметров, то половина всего перепада давления тратится на продвижение жидкости в пористой среде в зоне вокруг скважины радиусом всего менее шести метров. Для однородного пласта расчет распределения давления между стенкой и контуром питания скважины удобно вести по формуле:
|
|
|
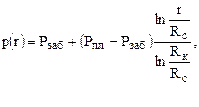(4.2)
где р(r) — давление в пласте на расстоянии r от центра скважины.
Приведенный пример ярко иллюстрирует тот факт, что ПЗП играет определяющую роль в притоке жидкости к скважине. Поэтому незначительное ухудшение проницаемости в этой зоне приводит к существенному снижению величины притока в скважину, что равносильно соответствующему снижению ее дебита.
Условия притока жидкости или газа в реальную скважину отличаются от притока в гидродинамически совершенную скважину тем, что в прискважинной зоне пласта и на боковой поверхности реальных скважин возникают дополнительные фильтрационные сопротивления из-за искривления и сгущения линий токов. Целесообразно выделять следующие три вида гидродинамического несовершенства скважин (рис.4.1):
1) по степени вскрытия пласта, когда скважина вскрывает продуктивный пласт не на всю толщину;
2) по характеру вскрытия пласта, когда связь пласта со скважиной осуществляется не через открытую боковую поверхность скважины, а только через перфорационные отверстия в обсадной колонне;
3) по качеству вскрытия пласта, когда проницаемость пористой среды в прискважинной зоне снижена по отношению к естественной проницаемости пласта.
Таким образом, физическая сущность гидродинамического несовершенства скважин заключается в том, что возникают дополнительные фильтрационные сопротивления, а на преодоление возникших сопротивлений приходится затрачивать то или иное количество располагаемой депрессии. Последнее обстоятельство ведет не только к снижению дебита скважин, но и к нерациональному использованию пластовой энергии.
|
|
|
Формулы притока несжимаемой жидкости в гидродинамически несовершенные скважины, имеющие несовершенство по одному какому-либо виду, могут быть записаны в следующем виде:
, (4.3)
, (4.4)
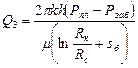, (4.5)
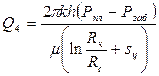, (4.6)
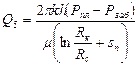, (4.7)
где: с1 — безразмерный коэффициент, учитывающий дополнительные фильтрационные сопротивления из-за несовершенства скважины по степени вскрытия продуктивного пласта;
с2 — безразмерный коэффициент, учитывающий дополнительные фильтрационные сопротивления из-за несовершенства скважины по характеру вскрытия продуктивного пласта (перфорация);
sб — безразмерный коэффициент, учитывающий дополнительные фильтрационные сопротивления из-за несовершенства скважины по качеству вскрытия продуктивного пласта бурением (скин-эффект из-за ухудшения проницаемости породы при первичном вскрытии пласта бурением);
sц — безразмерный коэффициент, учитывающий дополнительные фильтрационные сопротивления из-за несовершенства скважины по качеству цементирования (скин-эффект из-за ухудшения проницаемости породы при цементировании обсадной колонны);
sп — безразмерный коэффициент, учитывающий дополнительные фильтрационные сопротивления из-за несовершенства скважины по качеству вскрытия продуктивного пласта перфорацией (скин-эффект из-за ухудшения проницаемости породы при перфорации скважины)
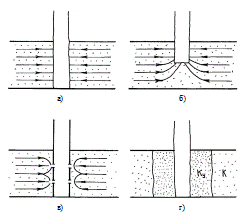
Рис. 4.1. Схематичное изображение гидродинамически совершенной и гидродинамически несовершенных скважин:
а) совершенная скважина;
б) несовершенная скважина по степени вскрытия пласта;
в) несовершенная скважина по характеру вскрытия пласта;
г) несовершенная скважина по качеству вскрытия пласта
(kу—проницаемость ПЗП, k —проницаемость удаленной зоны пласта)
В формуле (4.3) основные и дополнительные фильтрационные сопротивления в зоне дренирования соответственно равны:
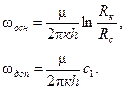
Однако, если скважина одновременно является гидродинамически несовершенной по двум и более видам, то учет этого обстоятельства в формулах притока простым сложением безразмерных фильтрационных сопротивлений может привести к существенным ошибкам, хотя ряд авторов таким образом поступали. В целях упрощения рассматриваемого вопроса так ранее поступал и автор этого учебного пособия. Дело в том, что не существует методик точного учета взаимодействия видов гидродинамического несовершенства между собой, хотя такое взаимодействие имеется. Например, проф. И.Т. Мищенко показал [13], что при некоторых допущениях суммарный коэффициент дополнительных фильтрационных сопротивлений, одновременно учитывающий несовершенство по степени (бурение) и характеру (перфорация) вскрытия пласта может быть определен по следующей формуле:
|
|
|
, (4.8)
где h' — относительное вскрытие продуктивного пласта бурением.
Формула притока (дебита скважины) в этом случае будет иметь вид:
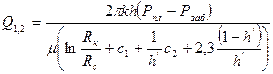. (4.9)
Логично предположить, что если видов несовершенства будет еще больше, то их совместное взаимодействие еще больше затруднит приток в скважину.
Для расчетов притока жидкости или газа к системе взаимодействующих гидродинамически несовершенных скважин имеет важное значение понятие приведенного радиуса (Rпр). Приведенным радиусом называется радиус такой фиктивной совершенной скважины, величина притока в которую при прочих одинаковых условиях равна величине притока в реальную гидродинамически несовершенную скважину. На основании данного определения формулу, например, (4.9) можно записать в виде:
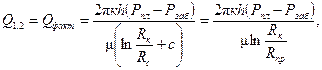(4.10)
где Qфакт — фактический дебит скважины.
Из последнего равенства легко получается выражение для приведенного радиуса: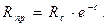 
Подстановка в формулы притока приведенного радиуса вместо действительного радиуса скважины обеспечивает замену одной реальной или системы реальных скважин их гидродинамическими эквивалентами — совершенными скважинами с фиктивными (приведенными) радиусами. Такой прием значительно упрощает гидродинамические расчеты, поскольку вместо сложных расчетно-аналитических зависимостей, описывающих приток в реальные гидродинамически несовершенные скважины, становится возможным применять простые формулы Дюпюи для гидродинамически совершенных скважин. Однако для этого нужно знать или величину коэффициента гидродинамического совершенства скважин, или величину безразмерных коэффициентов дополнительных фильтрационных сопротивлений.
|
|
|
Степень гидродинамической связи пласта и скважины характеризуется коэффициентом гидродинамического совершенства (φ), под которым понимают отношение фактического дебита (притока) скважины к дебиту (притоку) этой же скважины, если бы она была гидродинамически совершенной (т.е. если бы скважина, при прочих одинаковых условиях, имела открытый забой полностью вскрытого бурением пласта и естественную проницаемость пористой среды в ПЗП). Из этого определения и с учетом формул (4.1) и (4.10) следует, что: 
(4.1)
Коэффициент гидродинамического совершенства является одной из важнейших гидродинамических характеристик скважины, поэтому подлежит обязательному определению для каждой скважины наравне с коэффициентом продуктивности.
Из формул (4.10) и (4.11) легко получается выражение для определения приведенного радиуса:
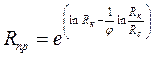. (4.12)
Из этих же формул следует, что:
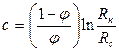. (4.13)
Строение пористой среды вокруг скважины и состояние ее забоя в реальном случае может иметь значительно более сложную картину, чем было рассмотрено выше (см., например, рис. 2.4 и 4.1). Соответственно столь сложной будет и гидродинамическая картина притока в реальную гидродинамически несовершенную скважину.
|
|
|
