 |
Методики определения гидродинамического совершенства скважин
|
|
|
|
С.107
В.И. Щуров применил метод электрогидродинамических аналогий (ЭГДА) с целью экспериментального изучения влияния степени и характера вскрытия пласта на дебит скважины. Был использован гладкий цилиндрический электрод в качестве электрической модели скважины с открытым забоем и цилиндр из токонепроводящего материала с вмонтированными цилиндрическими электродами правильной формы в качестве модели перфорированной скважины. Сравнение протекающих токов при последовательном помещении этих моделей в токопроводящую среду (электролит), геометрически подобную круговому пласту, позволило определить возникающие омические сопротивления, а от последних по ЭГДА перейти к фильтрационным сопротивлениям. В результате обработки экспериментальных данных были найдены значения безразмерных коэффициентов с1 и с2 для различных условий вскрытия пласта и построены графики (известные графики Щурова), которые широко используются в практике и теории разведки и разработки месторождений. Следует заметить, что несовершенство скважин из-за снижения проницаемости породы в ПЗП В.И. Щуровым не моделировалось.
Нами проведена математическая обработка экспериментальных данных В.И. Щурова. В результате получены следующие формулы:
 (4.14)
(4.14)
 (4.15)
(4.15)
где: 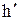 — относительное вскрытие пласта;
— относительное вскрытие пласта;
D — диаметр скважины, м;
l к — средняя длина перфорационных каналов, м;
d к — средний диаметр перфорационных каналов, м;
n — плотность перфорации, отв./м.
1.1. Методика определения коэффициентагидродинамического совершенства по исследованию
скважин на установившихся и неустановившихся режимах работы
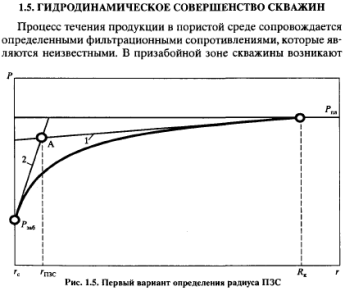
Изменение проницаемости породы прискважинной зоны, геометрия перфорационных каналов и забоя скважины с гидродинамической точки зрения имеют очень сложную картину и не поддаются точному математическому описанию. Действительно, для реальной скважины в промысловых условиях геофизики и технологи не знают, к примеру, каких размеров и формы получился каждый из перфорационных каналов, каковы степень и характер изменения проницаемости породы вокруг перфорационных каналов и т.п. Промысловые работники и исследователи также не имеют достоверной информации и о многих других параметрах, по которым можно было бы определить величины дополнительных фильтрационных сопротивлений. Поэтому определить коэффициент гидродинамического совершенства скважины по формуле, например, (4.11) обычно не представляется возможным, поскольку достоверно не известны фактические значения безразмерных коэффициентов, учитывающих дополнительные фильтрационные сопротивления в ПЗП и на стенке скважины, а также неизвестно влияние взаимодействия различных видов несовершенства.
|
|
|
Из сказанного следует, что нужна такая методика определения степени гидродинамического совершенства скважин, расчетные формулы которой не содержали бы в явном виде значений безразмерных коэффициентов дополнительных фильтрационных сопротивлений. Методика должна обладать необходимой точностью оценки и применима в любой период работы скважины, так как состояние пласта, прискважинной зоны, забоя с течением времени разработки месторождения и эксплуатации скважин также меняются. Такая методика, по всей вероятности, должна основываться на результатах гидродинамических исследований скважин.
Покажем, как на основе гидродинамических методов исследования скважин можно получить формулу для определения коэффициента гидродинамического совершенства. Введем в формулу притока (дебита) реальной скважины, описывающую плоскорадиальную фильтрацию жидкости по линейному закону, коэффициент гидропроводности (ε = кh/µ):
|
|
|
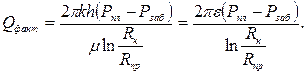
Переписав последнюю формулу относительно знаменателя:
 (4.17)
(4.17)
получаем, что влияние реально существующих безразмерных коэффициентов дополнительных фильтрационных сопротивлений может быть выражено через известные гидродинамические параметры — коэффициент гидропроводности пласта и коэффициент продуктивности скважины.
Подставляя (4.17) в (4.11), получаем следующую формулу для определения коэффициента гидродинамического совершенства:
 (4.18)
(4.18)
В полученной формуле величина коэффициента продуктивности (η) определяется по результатам гидродинамических исследований скважины на установившихся режимах работы, т.е. по индикаторной диаграмме (ИД). Величина коэффициента гидропроводности пласта (ε) определяется по углу наклона прямолинейного участка кривой восстановления давления (КВД), построенной в полулогарифмических координатах. Из теоретических основ гидродинамических исследований на установившихся и неустановившихся режимах работы следует, что коэффициент продуктивности, определенный по индикаторной диаграмме, характеризует всю зону дренирования — от контура питания до стенки скважины. Коэффициент гидропроводности, определенный по кривой восстановления давления, характеризует удаленную от скважины зону пласта с естественными (неизмененными из-за вскрытия продуктивного пласта или из-за применения методов воздействия на ПЗП) фильтрационными свойствами.
Таким образом, методика определения коэффициента гидродинамического совершенства скважин, основанная на формуле (4.18), построена на использовании результатов гидродинамических исследований скважин на установившихся и неустановившихся режимах работы. При этом в расчетах используются параметры, определяемые по результатам гидродинамических исследований скважин с наименьшей погрешностью.
Формула (4.18) справедлива также и для газовых скважин.
1.2. 4.4. Оценка гидродинамического совершенства скважин
по разностным кривым восстановления давления
Общепринято, что процесс восстановления забойного давления описывается уравнением (3.48) или (3.49). Графическое представление восстановления забойного давления (см. рис. 3.16) показывает, что в начальный период процесс восстановления давления осложнен влиянием некоторых факторов. Обычно начальный участок КВД, построенный в полулогарифмических координатах, не обрабатывают, хотя именно этот участок содержит информацию о прискважинной зоне пласта.
|
|
|
Понятно, что в любой момент времени величина депрессии (разница между пластовым и забойным давлениями) зависит от фильтрационных сопротивлений в зоне дренирования, поскольку упругое перераспределение давления есть не что иное как затухающая фильтрация из области с большим давлением в область с меньшим давлением (забой скважины, например). Зависеть — значит содержать информацию. В этой связи можно записать, что:
 , (4.19)
, (4.19)
где: Δp(t) — величина полного перепада давления в любой момент времени t;
Δpi(t) — перепады давления, затрачиваемые на те или иные фильтрационные сопротивления в момент времени t.
Чем более сложное строение зоны дренирования, тем большее число слагаемых может содержать уравнение (4.19).
Для обработки кривой восстановления давления П. Поллард предложил следующее уравнение:
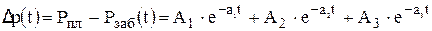 , (4.20)
, (4.20)
где:  — перепад давления, затрачиваемый на фильтрацию флюида в поровом пространстве (разность между пластовым давлением и давлением в трещинах в момент времени t);
— перепад давления, затрачиваемый на фильтрацию флюида в поровом пространстве (разность между пластовым давлением и давлением в трещинах в момент времени t);
 — перепад давления, затрачиваемый на течение флюида в трещинах;
— перепад давления, затрачиваемый на течение флюида в трещинах;
 — перепад давления, затрачиваемый флюидом на фильтрацию в ПЗП;
— перепад давления, затрачиваемый флюидом на фильтрацию в ПЗП;
А1, А2, А3, а1, а2, а3 — постоянные коэффициенты при условии, что пластовое давление больше давления насыщения жидкости газом (коэффициенты а1, а2, а3 связаны между собой соотношением а1 < а2 < а3).
Коэффициент А3 определяется выражением:
 . (4.21)
. (4.21)
Из (4.21) видно, что коэффициент в числителе последнего слагаемого уравнения (4.20) определяется величиной установившейся депрессии (перед мгновенным закрытием скважины на исследование) и величинами подобных коэффициентов предыдущих слагаемых.
Графическое представление уравнения (4.20) после логарифмирования показано на рис. 4.2. Кривую на этом рисунке можно поделить на три участка. Первый участок при малых значениях времени, обладая высокой динамичностью, характеризует потери давления в прискважинной зоне пласта. Средний участок характеризует движение флюида в трещинах (если таковые имеются). Конечный участок (участок кривой при больших значениях времени) соответствует потерям давления в поровом пространстве блоков.
|
|
|
Последовательность обработки замеров давления во времени, полученных при исследовании скважины, следующая:
а) строится кривая в координатах  ;
;
б) по конечному участку кривой проводится прямая линия до пересечения с осью ординат, определяется величина ln А1;
в) определяется значение коэффициента А1 по величине ln А1;
г) определяется значение а1 как тангенс угла наклона α1 прямой линии к горизонтали;
д) для произвольно взятых значений времени определяется разница 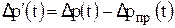 . Здесь
. Здесь  — значения перепада давления для прямой линии. Чем больше взято значений времени, тем точнее будут дальнейшие построения и вычисления;
— значения перепада давления для прямой линии. Чем больше взято значений времени, тем точнее будут дальнейшие построения и вычисления;
е) строится разностная кривая в координатах  (рис. 4.3);
(рис. 4.3);
ж) по конечному участку разностной кривой проводится прямая линия до пересечения с осью  ;
;
з) определяется значение коэффициента А2 по величине  ;
;
и) определяется значение а2 как тангенс угла наклона α2 прямой линии к горизонтали;
к) для любого значения времени определяется доля каждого члена в уравнении (4.20);
л) делается вывод об условиях фильтрации флюида в зоне дренирования.
Упростим задачу. Пусть продуктивный пласт — гранулярный, т.е. трещины отсутствуют и затраты давления на движение в трещинах тоже отсутствуют (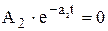 ), тогда уравнение (4.20) упростится и примет вид:
), тогда уравнение (4.20) упростится и примет вид:
 . (4.22)
. (4.22)


Рис. 4.2. Основная кривая восстановления давления







|
|

|


Рис.4.3. Разностная кривая восстановления давления
Из уравнения (4.22) следует, что полный перепад давления в любой момент времени расходуется только на фильтрацию в поровом пространстве от контура питания до ПЗП и на преодоление сопротивлений в ПЗП.
Обозначим перепад давления, затрачиваемый на фильтрацию флюида в прискважинной зоне пласта, через ΔрПЗП(t). С учетом этого обозначения уравнение (4.22) также несколько упростится и запишется в виде:
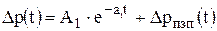 . (4.23)
. (4.23)
Обработка КВД в этом случае ограничивается только построениями в координатах  (см. рис. 4.2) и определением по построенному графику коэффициентов А1 и а1. Далее для любого значения времени определяется доля каждого члена уравнения (4.23) в общих затратах на фильтрацию флюида.
(см. рис. 4.2) и определением по построенному графику коэффициентов А1 и а1. Далее для любого значения времени определяется доля каждого члена уравнения (4.23) в общих затратах на фильтрацию флюида.
Полученную по изложенной методике долю ΔрПЗП(t) следует сравнить с распределением давления в пласте по уравнению (4.2). Из этого сравнения можно сделать качественный вывод о степени гидродинамического совершенства скважины и принять решение о том, следует ли применять методы воздействия на ПЗП.
|
|
|
Мищенко. Скважинная добыча нефти, с.26









|
|
|



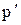 (t)
(t)