 |
Выпуклость и вогнутость функции
|
|
|
|
Пусть функция f (x) имеет производную в каждой точке промежутка (a; b). Если на промежутке (a; b) график функции f (x) расположен выше любой своей касательной, проведенной в точке этого промежутка, то функция называется вогнутой на этом промежутке (иногда говорят "выпуклой вниз") (рис. 11).
Если на промежутке (a; b) график функции f (x) расположен ниже любой своей касательной, проведенной в точке этого промежутка, то функция называется выпуклой на этом промежутке (иногда говорят "выпуклой вверх") (рис. 12).
Рис. 11 Рис. 12
Точка x 0 называется точкой перегиба функции f (x), если в этой точке функция имеет производную и существуют два промежутка: (a; x 0) и (x 0; b), на одном из которых функция выпукла, а на другом вогнута (рис. 13).
Будем называть функцию возрастающей в точке x 0, если она непрерывна в этой точке и возрастает в некоторой ее окрестности. Подобным образом можно определить функцию, убывающую в точке.
Приведем без доказательства важную для исследования функций теорему.
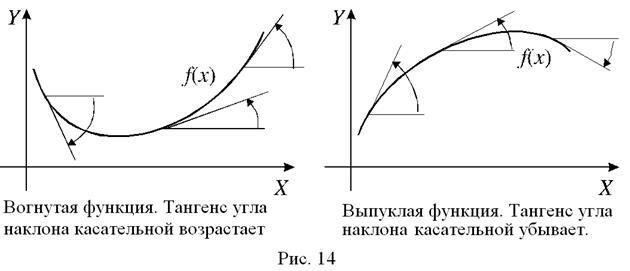
Если f¢¢ (x) > 0 на промежутке (a; b), то на этом промежутке функция f (x) вогнута. Если f¢¢ (x) < 0 на промежутке (a; b), то на этом промежутке функция f (x) выпукла.
Из положительности второй производной функции на промежутке следует возрастание первой производной на этом промежутке, а это, как показано на рисунке 14, – признак вогнутой функции. Аналогичным образом иллюстрируется второе утверждение теоремы.
Если x 0 – точка перегиба функции f (x), то f¢¢ (x 0) = 0.
Приведем другую формулировку достаточных условий экстремума функции.
Если в точке x 0 выполняются условия:
1) f¢ (x 0) = 0; f¢¢ (x 0) < 0, тогда x 0 – точка максимума;
2) f¢ (x 0) = 0; f¢¢ (x 0) > 0, тогда x 0 – точка минимума;
|
|
|
3) f¢ (x 0) = 0; f¢¢ (x 0) = 0, тогда вопрос о поведении функции в точке остается открытым. Здесь может быть экстремум, например в точке x 0 = 0 у функции y = x 4, но может его не быть, например в точке x 0 = 0 у функции y = x 5. В этом случае для решения вопроса о наличии экстремума в стационарной точке можно использовать достаточные условия экстремума, приведенные выше.
Рассмотрим пример из микроэкономики.
В количественной теории полезности предполагается, что потребитель может дать количественную оценку (в некоторых единицах измерения) полезности любого количества потребляемого им товара.
Это означает существование функции полезности TU аргумента Q – количества купленного товара. Введём понятие предельной полезности, как добавочной полезности, прибавляемой каждой последней порцией товара. Далее построим двумерную систему координат, 
откладывая по горизонтальной оси
количество потребляемого товара Q, а по вертикальной оси – общую полезность TU, как это сделано на рисунке 15. В этой системе координат проведем график функции TU = TU (Q). Точка Q 0 на горизонтальной оси означает количество приобретенного товара, величина D Q –добавочный приобретенный товар. Разность D TU = TU (Q 0 + D Q) – TU (Q 0) ‑ добавочная полезность, полученная от покупки “довеска” D Q. Тогда добавочная полезность от последней приобретенной порции (или единицы количества) товара вычисляется по формуле D TU / D Q (Курс экономической теории. Под общей редакцией проф. Чепурина М.Н. 1995, стр. 122). Эта дробь, как можно видеть, зависит от величины D Q. Если здесь перейти к пределу при D Q ® 0, то получится формула для определения предельной полезности MU:
.
Это означает, что предельная полезность равна производной функции полезности TU (Q). Закон убывающей предельной полезности сводится к уменьшению этой производной с ростом величины Q. Отсюда следует выпуклость графика функции TU (Q). Понятие функции полезности и представление предельной полезности в виде производной этой функции широко используется в математической экономике.
|
|
|
Асимптоты графика функции
Пусть функция 
определена для всех 
(либо 
). Если существуют такие числа 
и 
, что 
(либо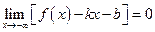 
), то прямая 
называется асимптотой графика функции при 
(при 
).
Геометрически асимптота – есть прямая, к которой неограниченно приближается уходящая в бесконечность ветвь графика функции.
Уравнение наклонной асимптоты (нахождение и ).
По определению должен существовать предел или 
, но тогда необходимо, чтобы 
. Следовательно 
. Если этот предел существует, тогда из существующего исходного предела получим 
. Если оба эти предела существуют, то уравнение – уравнение наклонной (правой) асимптоты (рис. 16).
Рис. 16
Аналогично решается вопрос о наличии левой наклонной асимптоты, при .
Если же существует 
и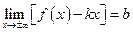 
, то уравнение – уравнение двухсторонней асимптоты (рис. 17).
Рис. 17
Возможен случай, что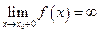 
, либо 
. В таких случаях прямую 
называют вертикальной асимптотой (рис. 18).
Рис. 18
|
|
|
