Формула интегрирования по частям

Пусть u (x) и v (x) — дифференцируемые на некотором промежутке функции. Тогда

(uv) ¢ = u¢v + v¢u

Отсюда следует

ò (uv) ¢dx = ò (u¢v + v¢u) dx = ò u¢v dx + ò v¢u dx

или

ò uv¢ dx = uv – ò u¢v dx.

Отсюда следует формула, которая называется формулой интегрирования по частям:

ò u (x) dv (x) = u (x) v (x) – ò v (x) du (x)

Приведем примеры применения формулы интегрирования по частям.

Примеры. 1. I = ò x cos x dx. Пусть u = x; dv = cos x dx, тогда du = dx; v = sin x. Отсюда по формуле интегрирования по частям получается:

I = x sin x – ò sin x dx = x sin x + cos x + C.

2. I = ò (x² – 3 x + 2) e^5xdx. Пусть x² – 3 x + 2 = u; e^5xdx = dv. Тогда
du = (2 x – 3) dx; .

.

К последнему интегралу применим метод интегрирования по частям, полагая 2 x - 3 = u; e^5xdx = dv. Отсюда следует: du = 2 dx; , и окончательно получаем:

.

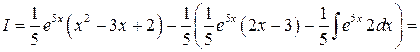
3. ;

;

.

В заключение покажем метод вычисления неопределенного интеграла, стоящего в приведенной выше таблице под номером 12:

.

Представим дробь в виде суммы двух дробей: и 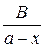, и попытаемся найти неизвестные величины параметров A и B. Из равенства получим систему уравнений

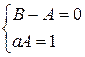
с решением . Отсюда следует:

.

Полученный интеграл в обиходе обычно называют “высоким логарифмом”. Метод, которым он был найден, называется методом “неопределенных коэффициентов”. Этот метод применяется при вычислении интегралов от дробей с числителем и знаменателем в виде многочленов.

 

 

Определенный интеграл

Пусть на промежутке [ a; b ] задана функция f (x). Будем считать функцию непрерывной, хотя это не обязательно. Выберем на промежутке [ a; b ] произвольные числа x ₁, x ₂, x ₃, ¼, x_{n -1}, удовлетворяющие условию:
a < x ₁,< x ₂<¼< x_{n -1},< b. Эти числа разбивают промежуток [ a; b ] на n более мелких промежутков: [ a; x ₁], [ x ₁; x ₂], ¼ [ x_{n -1}; b ]. На каждом из этих промежутков выберем произвольно по одной точке: c ₁Î[ a; x ₁], c ₂Î[ x ₁; x ₂], ¼ c_n Î[ x_{n -1}; b ].

Введем обозначения:D x ₁ = x ₁ – a; D x ₂ = x ₂ – x ₁; ¼ D x_n = b – x_{n- 1}.

Составим сумму: .

Она называется интегральной суммой функции f (x) по промежутку [ a; b ]. Очевидно, что интегральная сумма зависит от способа разбиения промежутка и от выбора точек c_i.

Каждое слагаемое интеграль­ной суммы представляет собой площадь прямоугольника, покрытого штриховкой на рисунке 19.

Введем обозначение: l = max(D x_i), i = 1, 2, ¼ n.. Величину l иногда называют параметром разбиения.

Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что величина l стремится к нулю. Определенным интегралом

от функции по промежутку [ a; b ] называется предел, к которому стремится интегральная сумма при этом процессе, если предел существует:

.

Если такой предел существует, то он не зависит от первоначального разбиения промежутка [ a; b ] и выбора точек c_i.

Рис. 20

Число a называется нижним пределом интегрирования, а число b ¾ верхним пределом интегриро­вания.

Рассмотрим фигуру, ограни­ченную графиком непрерывной, неотрицательной на промежутке [ a; b ] функции f (x), отрезком [ a; b ] оси X, и прямыми x = a; x = b. Такую фигуру называют криволинейной трапецией. На рисунке 20 криволинейная трапеция выделена штриховкой. Площадь S этой трапеции определяется формулой

Рис. 21

.

Если f (x) < 0 во всех точках промежутка [ a; b ] и непрерывна на этом промежутке (например, как изображено на рисунке 21), то площадь криволинейной трапеции, ограниченной отрезком [ a; b ] горизонтальной оси координат, прямыми x = a; x = b и графиком функции y = f (x), определяется формулой

.

Перечислим свойства определенного интеграла:

1) (здесь k ‑ произвольное число);

2) ;

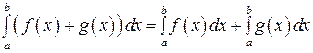3) ;

4) Если cÎ [ a; b ], то .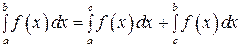

Из этих свойств следует, например, что .

Все приведенные выше свойства непосредственно следуют из определения определенного интеграла.

Рис. 22

Оказывается, что формула из пункта 4 справедлива и тогда, когда cÏ [ a; b ]. Пусть, например, c>b, как изображено на рисунке 22. В этом случае верны равенства

.

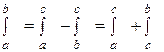⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: