 |
Построение логических схем.
|
|
|
|
При построении логических схем пользуются таким термином как логическая ячейка, которую можно представить в следующем виде:
 |
Sn.
|
An.
 |
Rn.
Cn.
Где её компонентами являются следующие значения:
Sn.- Поставленная задача;
An.- Исходные данные;
Cn.- Ограничения;
Mn.- Модуль;
Tn.- Решаемая процедура;
Kn.- Оценка качества;
Rn.- Проектное решение.
Рассмотрев, что собой представляет логическая ячейка перейдём к рассмотрению задач в данном курсовом проекте.
Логическая ячейка 1.
 |
S1.
|
A1.
R1.
C1.
S1. -Вычисление всякого В-сплайна N–ой степени.
A1. -Bni(x) -наиболее употребительный базис В-сплайн N-ой степени.
- bi -некоторые постоянные коэффициенты.
C1. - i = -n, … N-1.
T1. - S(x) -всякий сплайн N-ой степени.
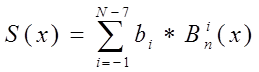
R1. - S(x) –всякий сплайн N-ой степени.
Логическая ячейка 2.
 |
S2.
|
A2.
R2.
C2.
|
S2. - Вычисление В-сплайна нулевой степени.
A2. - Х - координата функции по оси абсцисс.
C2. - ограничения имеют вид:
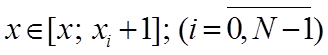
T2. - В-сплайн нулевой степени.
|
|
|
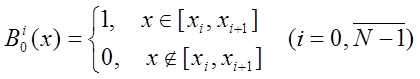
R2. - В-сплайн нулевой степени.
Логическая ячейка 3.
 |
S3.
|
A3.
R3.
C3.
S3. - Получение нового разбиения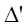 
и для него рекуррентное соотношение.
A3. - Входные данные x, xi, xi+n, xi+1, xi+n+1, Bin-1(x).
C3. - Новое разбиение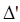 
,
(x-n<x-n+1<…<x-1<x0<x1<…<xN<xN+1<…<xN+n),
n=1,2,…;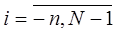 
;
T3. - Рекуррентное соотношение.
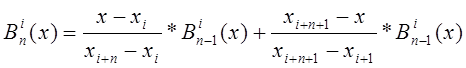
R3. - Bin(x) –рекуррентное соотношение на выходе ячейки.
Логическая ячейка 4.
 |
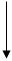S4.
|
A4.
R4.
C4.
S4. - Хранение предыдущего значения сплайна Bin-1(x).
A4. - Предыдущее значение сплайна Bin-1(x).
M4. - Модуль хранения значения со входа ячейки.
T4. - Передача хранимого значения на выход.
R4. - Предыдущее значение сплайна Bin-1(x).
Логическая ячейка 5.
|
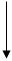S5.
|
A5.
R5.
C5.
S5. - Вычисление В-сплайна третей степени Bi3(x).
A5. - t -размер шага движения по оси абсцисс.
C5. - ограничения:
; x < xi-2;
xi-2 < x < xi-1;
xi-1 < x < xi;
xi < x < xi+1;
xi+1 < x < xi+2;
xi+2 < x.
T5. - Выражение В-сплайна третей степени.
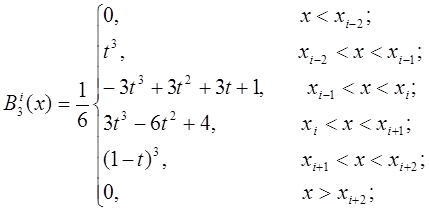
R5. – Выражение В-сплайна третей степени Bi3(x).
|
|
|
Логическая ячейка 6.
 |
S6.
|
A6.
R6.
C6.
S6. - Вычисление В-сплайна пятой степени Bi5(x).
A6. - t -размер шага движения по оси абсцисс.
C6. - ограничения:
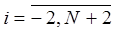; x < xi-3;
xi-3 < x < xi-2;
xi-2 < x < xi-1;
xi-1 < x < xi;
xi < x < xi+1;
xi+1 < x < xi+2;
xi+2 < x < xi+3;
xi+3 < x.
T6. - Выражение В-сплайна пятой степени.
R6. - Выражение В-сплайна пятой степени Bi5(x).
Логическая ячейка 7.
 |
S7.
|
A7.
R7.
C7.
S7. - Определение количества шагов на заданном интервале.
A7. - h - шаг разбиения по оси абсцисс.
Рассматриваемый интервал: (xi, xi+1).
T7. - Количество шагов на заданном интервале t.
;
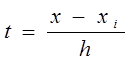R7. - Количество шагов на заданном интервале h.
На рисунке 3 представлена логическая схема нашей системы.
СХЕМА АНАЛИЗА ПРОЕКТА.
Программный продукт составлен на модульном принципе. Он состоит из отдельных модулей (подпрограмм) реализующих определённые части вычислительного процесса. Модули по своему назначению делятся на модули специального и общего назначения.
Модули специального назначения (модули 1 и 6) зависят от вида граничных условий, нагрузок, структуры пакета слоёв, геометрических характеристик конической оболочки, способа выбора точек коллокации и т.д.
Структурная схема программы с указанием связей между её модулями показана на рисунке 4.
Выполнение программы начинается с головной (модуль 1) где задаётся вся исходная информация с клавиатуры пользователем или из базы данных. После задания исходной информации подключаем к работе специальные модули 2 и 3, вычисляющие, соответственно, сплайны 3-й и 5-й степени на заданных отрезках. После этого подключаем к работе специальный модуль 4, который, вычисляет сплайн нулевой степени сплайны 3-й и 5-й степени находит конечный В-сплайн. Специальный модуль 5 производит всю необходимую работу с матрицами. Данные, полученные после работы модулей 4 и 5, используются в программе вычисления правых частей системы обыкновенных дифференциальных уравнений (модуль 6). После задания и получения всей исходной информации управление передаётся модулю 7, в котором реализована вычислительная схема метода дискретной ортогонализации.
|
|
|
В модулях общего назначения реализуется часть вычислительного процесса, являющаяся неизменной для всех задач данного класса. В этих модулях производится вычисление правой части системы дифференциальных уравнений по заданной информации о геометрических и механических характеристиках оболочки.
Рис.4. Структурная схема программы.
К модулям общего назначения относятся:
1) Модуль 6. В нём производится вычисление вектора правых частей системы обыкновенных дифференциальных уравнений по заданным геометрическим и механическим параметрам оболочки.
2) Модуль 7. Этот модуль является основной частью программы. В нём реализуется алгоритм решения линейной краевой задачи, производится управление работой остальных модулей.
3) Модуль 8. Производит вывод на печать значений разрешающих функций в точках выдачи результатов.
4) Модуль 9. В этом модуле осуществляется решение систем линейных алгебраических уравнений с несколькими правыми частями методом Гаусса с выбором главного элемента.
5) Модуль 10. В теле данного модуля по заданной информации (в матричном виде) головной программы производится формирование расширенных матриц левых и правых граничных условий.
При этом возможно получение следующих результатов:
1) Построение аналитического решения задачи об изгибе ортотропных конических оболочек осесимметричного строения под действием нормальной поверхностной нагрузки и температурного поля с помощью гипергеометрических функций.
|
|
|
2) Разработка методики численного решения двумерных краевых задач о деформации разомкнутых и замкнутых ортотропных конических оболочек переменной в двух координатных направлениях жёсткости, основанной на использовании сплайн-коллокации.
3) На основе разрабатываемого подхода к решению двумерных краевых задач построен алгоритм численного решения задач о деформации ортотропных замкнутых и разомкнутых конических оболочек вращения переменной жёсткости.
4) Исследования напряжённо-деформированного состояния ряда конических оболочек в зависимости от их геометрических и механических параметров, видов нагрузки и граничных условий.
|
R2. S4.
|
C2.
A4.
R4.
S7. C4.
S5. S1.
|
|
|
R7. A5. R1.
R5.
C7. C5. S3. C1.
| | ||||
| ||||
A3.
R3.
S6. C3.
| | |||
| |||
A6.
R6.
C6.
Рис.3. Логическая схема проектирования данной системы.
|
|
|
