 |
Разработка регрессионных моделей оценки состояния транспортного потока
|
|
|
|
При описании характера или структуры взаимосвязей существующих между изучаемыми явлениями и показателями, в случае, если эти зависимости выявляются на основании статистического наблюдения за анализируемыми событиями или переменными, имеет место проблема статистического исследования зависимостей.
Общая задача статистического исследования зависимости может быть сформулирована следующим образом: по результатам измерений исследуемых переменных на объектах, анализируемой совокупности построить такую функцию, которая позволила бы наилучшим образом восстанавливать значения результирующих переменных по заданным значениям объясняющих переменных. Весть процесс исследования можно разделить на этапы:
1) Постановочный.
2) Информационный.
3) Корреляционный анализ.
4) Анализ мультиколлинеарности предсказывающих переменных и отбор наиболее информативных.
5) Определение класса допустимых решений.
6) Вычисление оценок неизвестных параметров входящих в исследуемое уравнение статистической связи.
7) Анализ точности полученных уравнений связи.
По данным моделирования дорожного движения транспортного потока на участке УДС рассмотрим возможность разработки регрессионной модели, оценки состояния транспортного потока.
Для этого, по данным характеристик транспортного потока, построим матрицу парных корреляций, содержащую значения множественного коэффициента корреляции.

Рисунок 3.1 Матрица парных корреляций
Проанализируем матрицу парной корреляций:
1) Наличие сильной связи между критериями (RZ,stop = 0,767) подтверждает тот факт что существует общие факторы влияющие на их формирование.
2) Проанализируем влияние факторов на каждый критерий:
|
|
|
а) С задержками движения Z сильно коррелируют скорость движения V (R ZV = -0.777) и интенсивность N (R ZN = -0.809). Возмножена разработка модели Z=f(N,V).
Проверим наличие эффекта мультиколлинеарности факторов, │rN,V│= │0.88│= 0.88 > 0.8 = эффект есть. Будет, разрабатывается модель Z =f(N).
б) С количеством остановок stop сильно коррелируют скорость движения V (Z stopV = -0,857) и сильно интенсивность N (Z stopN = -0,840). Возмножена разработка модели Z=f(N,V).
Проверим наличие эффекта мультиколлинеарности факторов, │rN,V│= │0.88│= 0.88 > 0.8 = эффект есть. Будет, разрабатывается модель stop =φ(V).
По результатам анализа корреляционной матрицы пришли к выводу о целесообразности разработки моделей линейных регрессий позволяющих оценить задержки движения в зависимости от изменения интенсивности и количество остановок в зависимости от изменения скорости движения.
Разработка линейной модели задержек Z=f(N)
По результатам анализа корреляционной матрицы пришли к выводу о целесообразности разработки модели линейной регрессии, позволяющей оценить задержки движения в зависимости от изменения скорости движения.

Рисунок 3.2 Показатели корреляционной связи задержек движения от интенсивности
Оценка коэффициентов уравнения и оценка значимости
z=f(N);
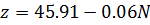 (1)
(1)
Доверительные интервалы
32.61<а< 59.20
-0.08<б><-0.038
Значимость вычислимых коэффициентов оцениваем с помощью критерия Стьюдента
Для коэффициента «а» наблюдаемое значение критерия tнабла =7.25
Для коэффициента «б» наблюдаемое значение критерия tнаблб = 0.01
Так как │ tнабла│ =│ 7.25 │; │tнаблб│ =│ 0.01│; больше t0,05 18 = 2,110 то все коэффициента признаются значимыми.
Оцениваем адекватность разработанной модели

Рисунок 3.3 показатели множественной корреляционной связи
1) Multiple R = 0.81;
2) Multiple R? = 0.66;
3) Adjusted R? = 0.64;
4) F = 32.27;
5) P = 0.000015;
|
|
|
6) df Model = 1;
7) df Residual = 18.
Согласно найденным значениям показателей корреляционной связи разработанная модель объясняет 64 % вариаций задержек движения за счет влияния скорости движения. Остальные 36% остаются, не объяснимы, на их формирование оказывают влияние другие не учетные в модели факторы.
Разработанная модель является статистически значимой, так как
Fнабл = 32.27> F0,05;1; 18 = 3.59 и может использоваться для прогнозирования изменений задержек движения.

Рисунок 3.4 График функции 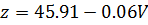
Разработка линейной модели задержек stop =φ(V)

Рисунок 3.5 Показатели корреляционной связи количества остановок от скорости движения
Оценка коэффициентов уравнения и оценка значимости
stop =φ(V);
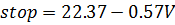 (2)
(2)
Доверительные интервалы
17.23<а<27.51
-0.74<б<0.40
Значимость вычислимых коэффициентов оцениваем с помощью критерия Стьюдента
Для коэффициента «а» наблюдаемое значение критерия tнабла = 9.14
Для коэффициента «б» наблюдаемое значение критерия tнаблб = -7.05
Так как │tнабла│ =│ 9.14│; │tнаблб│ =│ -7.05│; больше t0,05 18 = 2,110 то все коэффициенты признаются значимыми.
Оцениваем адекватность разработанной модели.

Рисунок 3.6 показатели множественной корреляционной связи
1) Multiple R = 0.86;
2) Multiple R? = 0.73;
3) Adjusted R? = 0.7;
4) F = 49.76;
5) P = 0.000001;
6) df Model = 1;
7) df Residual = 18.
Согласно найденным значениям показателей коррлеляционной связи разработанная модель объясняет 72 % вариаций задержек движения за счет влияния скорости движения. Остальные 28% остаются не объяснимы на их формирование оказывают влияние другие не учетные в модели факторы.
Разработанная модель является статистически значимой, так как
Fнабл = 49.76> F0,05;1; 18 = 3.24 и может использоваться для прогнозирования изменения количества остановок.

Рисунок 3.7 Графии функции 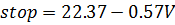
Заключение
В данной работе была проведена статистическая обработка данных: скорости движения и временных интервалов между автомобилями. По результатам этой обработки установлено что: средняя скорость автомобилей в транспортном потоке равна 30,43 км/ч, основная часть значений колеблется в диапазоне 30±3 км/ч, т. е. в интервале (27;33); интенсивность изменения значений скорости достаточно не высокая (10%), совокупность скоростей достаточно однородная. Среднее значение временного интервала между последовательно движущимися автомобилями, равно 1,48с., основная часть значений задержек колеблется в диапазоне 1,4 ±1,3, т. е. в интервале (0,1;2,7); интенсивность изменения значений временного интервала автомобилей высокая (89.54), совокупность скоростей неоднородная.
|
|
|
Так же проверили статистическую гипотезу о законе распределения скорости и временных интервалов движения транспортных средств. На основании этой проверки выясним, что скорость распределяется по нормальному закону с параметрами α= 30.43, σ= 1.79; а временной интервал движения по экспоненциальному закону, с параметром λ= 0.68.
Провели корреляционный анализ по данным: интенсивности, скорости, задержек движения и количества остановок. По результатам анализа корреляционной матрицы пришли к выводу о целесообразности разработки моделей вида: z=f(N), stop =φ(V).
Модель Z=45,91-0,06N объясняет 64% вариации задержек движения, за счет влияния интенсивности движения, а разработанная модель Stop=22,37-0,57V объясняет 72% вариации количества остановок, за счет влияния скорости движения.
В подтверждение выше сказанному приведены графики изменения Z=45,91-0,06N и Stop=22,37-0,57V.
СПИСОК ЛИТЕРАТУРЫ
1. Дрю Д. Теория транспортных потоков и управление ими. "Траспорт", 1972 г.
2. Кочерга В.Г., Зырянов В.В., Коноплянко В.И. Интеллектуальные транспортные системы в дорожном движении: Учебное пособие. - Ростов н/Д: Рост. гос. строит, ун-т, 2001. – 108 с.
3. Коноплянко, Косалапов, Гуджоян, Зырянов В.В«Организация и безопасность движения».
4. Кременец Ю.А. Технические средства организации дорожного движения. М. "Траспорт", 1990, 255с.
5. Клинковштейн Г. И., Афанасьев М. Б. Организация дорожного движения: Учеб. для вузов. — 5-е изд., перераб. и доп. — М: Транспорт, 2001 г.
6. Организация и безопасность дорожного движения. Автор: Владимир Коноплянко. Издательство: Высшая школа Серия: Для высших учебных заведений 2007 г.
7. Самойлов Д.С., Юдин В.А. Организация и безопасность городского движения. М. "Высшая школа", 1922, 256с.
|
|
|
8. Хейт Ф. Математическая теория транспортных потоков. 1966 г.
9. http://www.masters.donntu.edu.ua
10. http://www.nestor.minsk.by/sn/2009/31/93101.html
|
|
|


