 |
Эквивалентные преобразования в линейных пассивных цепях
|
|
|
|
Для упрощения анализа работы разветвленных линейных электрических цепей целесообразно применять различные способы, основанные на эквивалентных преобразованиях одних участков цепи в другие.
Под эквивалентным преобразованием понимают такую замену одного участка цепи на другой, при которой все внешние сигналы (токи и напряжения) по отношению к рассматриваемому участку цепи остаются без изменений.
Наиболее простым методом преобразования цепи является сведение сложной по топологии (разветвленной) цепи к одноконтурной. Данный метод может быть использован в случае, когда в качестве реакции цепи в режиме постоянного тока рассматривают ток (напряжение) на входной паре зажимов, напряжение на участке цепи в виде параллельного соединения.
Простое сворачивание сложной цепи базируется на следствиях из первого и второго законов Кирхгофа. Рассмотрим суть такого эквивалентного преобразования на следующем примере.
Пример 1
Применяя метод простого сворачивания определить входной ток для цепи, изображенной на рис. 1.18.

Рис. 1.18
Приведенная на рисунке цепь является разветвленной и содержит два узла и три ветви. Отыскание искомой реакции по первому и второму законам Кирхгофа с применением закона Ома потребовало бы составления и решения системы трех уравнений электрического равновесия. Однако следует отметить, что поскольку реакция цепи на задающее напряжение источника ЭДС рассматривается на входной паре зажимов, то достаточным является отыскание общего сопротивления данной цепи со стороны входных зажимов. Применяя закон Ома, можно определить искомую реакцию в соответствии с выражением:
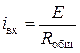 .
.
Так как участок цепи в виде пары ветвей, связывающих узлы 1 и 2, является параллельным соединением данных ветвей, обладающих сопротивлениями 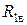 и
и  , то его можно заменить на эквивалентную ветвь с сопротивлением:
, то его можно заменить на эквивалентную ветвь с сопротивлением:
|
|
|
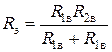 .
.
В свою очередь первая из ветвей представлена последовательным соединением двух резистивных элементов  и
и  , тогда в силу свойств последовательного соединения сопротивлением данной ветви задано выражением
, тогда в силу свойств последовательного соединения сопротивлением данной ветви задано выражением  . Сопротивление второй ветви, содержащей один резистивный элемент, определено как
. Сопротивление второй ветви, содержащей один резистивный элемент, определено как 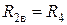 . С учетом сделанных замечаний:
. С учетом сделанных замечаний:
 .
.
На рис. 1.19 приведена схема замещения рассматриваемой цепи на основе выполненного эквивалентного преобразования.

Рис. 1.19
Как следует из рис. 1.19, из исходной трехконтурной цепи получили эквивалентную одноконтурную цепь.
Применяя в свою очередь замену двух последовательно соединенных резистивных элементов  и
и 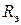 одним
одним  , приходим к схеме замещения цепи приведенной на рис. 1.20. Здесь:
, приходим к схеме замещения цепи приведенной на рис. 1.20. Здесь:
 .
.

Рис. 1.20
Окончательно для входного тока получаем выражение вида:
 .
.
Следующий метод эквивалентного преобразования цепи заключается в эквивалентной замене реального источника тока (рис. 1.21,б) на реальный источник напряжения (рис. 1.21, а) и наоборот.

Рис. 1.21
Преобразование одного источника в другой будет эквивалентным, если выполняются следующие условия:
 , (1.28)
, (1.28)
где  и
и  - задающие напряжение (ЭДС) и ток генератора напряжения (ЭДС) и генератора тока;
- задающие напряжение (ЭДС) и ток генератора напряжения (ЭДС) и генератора тока;  и
и  - внутренние сопротивления генератора тока и генератора ЭДС.
- внутренние сопротивления генератора тока и генератора ЭДС.
Эквивалентную замену одного источника электрической энергии на другой целесообразно применять в том случае, если искомая реакция представляет собой ток или напряжение ветви, не присоединенной к выходным зажимам генератора тока (напряжения).
Пример 2
Применяя эквивалентную замену источников энергии определить реакцию в виде напряжения на третьем резистивном элементе цепи, изображенной на рис. 1.22. Исходными данными к расчету являются: 
 .
.
|
|
|


Рис. 1.22
Произведем замену источника ЭДС на источник тока в соответствии с условиями (1.28). Схема замещения цепи приведена на рис. 1.23.

Рис. 1.23
Величина задающего тока равна  и внутреннее сопротивление эквивалентного генератора тока равно
и внутреннее сопротивление эквивалентного генератора тока равно  .
.
Теперь заменим параллельно соединенный участок цепи, состоящий из сопротивлений  и
и  эквивалентным сопротивлением
эквивалентным сопротивлением 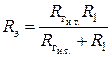 . Тогда схема замещения цепи имеет вид, приведенный на рис. 1.24.
. Тогда схема замещения цепи имеет вид, приведенный на рис. 1.24.


Рис. 1.24
Применим еще раз эквивалентную замену источник тока на источник ЭДС, в результате которой цепь имеет вид, изображенный на рис. 1.25.
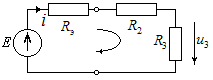
Рис. 1.25
Величина задающей ЭДС нового эквивалентного источника напряжения равна 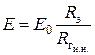 .
.
Таким образом, в результате проведенных эквивалентных преобразований разветвленная цепь сведена к одноконтурной. Теперь, применяя второй закон Кирхгофа и закон Ома, определим ток  в данной цепи и искомую реакцию
в данной цепи и искомую реакцию  .
.
 . (1.29)
. (1.29)
 . (1.30)
. (1.30)
В результате подстановки численных данных и произведенного расчета напряжение на третьем резистивном элементе составляет  .
.
Некоторые электрические цепи не поддаются простому свертыванию. К таким цепям относят так называемые мостовые цепи.
Получим соотношения, связывающие сопротивления сторон треугольника резистивных элементов и сопротивления лучей звезды резистивных элементов, обеспечивающие эквивалентную замену данных участков цепи друг на друга (рис. 1.26, а, б).
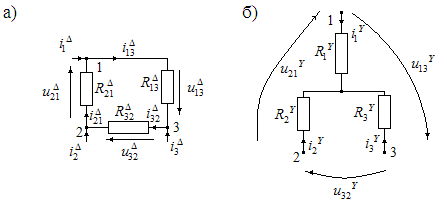
Рис. 1.26
Обозначим все токи и напряжения, соответствующие треугольнику сопротивлений, верхним индексом  , а соответствующие звезде сопротивлений – верхним индексом
, а соответствующие звезде сопротивлений – верхним индексом  . По условию эквивалентной замены все токи и напряжения во внешней цепи должны остаться неизменными. Тогда будут справедливы следующие соотношения
. По условию эквивалентной замены все токи и напряжения во внешней цепи должны остаться неизменными. Тогда будут справедливы следующие соотношения
 .(1.31)
.(1.31)
Запишем уравнение электрического равновесия по второму закону Кирхгофа для контура, образованного сторонами треугольника сопротивлений. Выберем направление обхода контура по часовой стрелке. Все напряжения на сопротивлениях  совпадают с направлением обхода контура. Тогда:
совпадают с направлением обхода контура. Тогда:
 .
.
С применением закона Ома приведем последнее уравнение к виду:
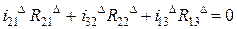 . (1.32)
. (1.32)
Составим уравнения электрического равновесия по первому закону Кирхгофа для рассматриваемого треугольника сопротивлений относительно узлов 1 и 2:
|
|
|
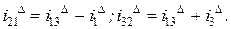 (1.33)
(1.33)
Подставим выражения (1.33) в уравнение (1.32) и решим полученное уравнение относительно тока  .
.

 (1.34)
(1.34)
По закону Ома:
 . (1.35)
. (1.35)
С другой стороны для звезды сопротивлений:
 . (1.36)
. (1.36)
С учетом условий эквивалентной замены приравняем друг к другу выражения (1.35) и (1.36), откуда находим:
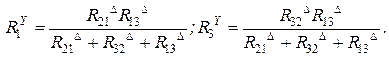 (1.37)
(1.37)
Для сопротивления второго луча звезды по аналогии можно получить выражение вида:
 . (1.38)
. (1.38)
Итак, получили систему уравнений вида:
 (1.39)
(1.39)
Решая данную систему уравнений относительно сопротивлений  , получаем следующий результат:
, получаем следующий результат:
 (1.40)
(1.40)
Пример 3
Применяя преобразование треугольника сопротивлений в звезду определить ток на входе рассматриваемой цепи.

Рис. 1.27
В данной цепи имеют место два треугольника сопротивлений  и
и  . Произведем эквивалентную замену треугольника сопротивлений
. Произведем эквивалентную замену треугольника сопротивлений  в звезду сопротивлений
в звезду сопротивлений  (рис. 1.28), где сопротивления лучей звезды находим в соответствии с выражениями (1.39)
(рис. 1.28), где сопротивления лучей звезды находим в соответствии с выражениями (1.39)
 (1.41)
(1.41)
Далее цепь подвергнем простому сворачиванию к одноконтурной цепи.

Рис. 1.28
Теперь параллельно соединенные ветви из резистивных элементов 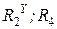 и
и 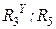 заменим эквивалентным сопротивлением
заменим эквивалентным сопротивлением
 . (1.42)
. (1.42)
В результате проведенных эквивалентных преобразований исходная мостовая схема приведена к простейшей одноконтурной цепи (рис. 1.29).

Рис. 1.29
Применяя следствия из второго закона Кирхгофа для последовательно соединенного участка цепи в виде двух сопротивлений  и
и 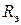 , получаем выражение для входного тока в виде:
, получаем выражение для входного тока в виде:
 , (1.43)
, (1.43)
где  и
и 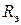 рассчитываются в соответствии с выражениями (1.41) и (1.42).
рассчитываются в соответствии с выражениями (1.41) и (1.42).
Анализ пассивных линейных цепей в ряде случаев может быть упрощен путем применения такого эквивалентного преобразования как перенос идеальных источников напряжения или тока.
Перенос источника ЭДС из какой-либо ветви, присоединенной к узлу, в другие ветви, присоединенные к этому же узлу, будет правомерен, если суммарные ЭДС контуров останутся без изменения.
Аналогично, перенос источника тока в другие ветви цепи будут правомерен для случая, когда суммарные задающие токи узлов остаются неизменными в результате осуществленного преобразования.
|
|
|
На рис. 1.30 и 1.31 показано, как следует осуществлять перенос идеальных источников ЭДС и тока в цепях.

Рис. 1.30

Рис. 1.31
Пример 4
Применяя эквивалентное преобразование в виде переноса идеального источника ЭДС в рассматриваемой цепи найти указанную на схеме цепи (рис. 1.32) реакцию.

Рис. 1.32
Осуществим перенос идеального источника ЭДС в ветви, соединяющие 1 и 3 узлы и 1 и 2 узлы. Тогда схема замещения цепи имеет вид (рис. 1.33)

Рис. 1.33
Теперь произведем эквивалентную замену реальных источников ЭДС на реальные источники тока с задающими токами  и
и  . Тогда схема замещения цепи имеет вид, приведенный на рис. 1.34.
. Тогда схема замещения цепи имеет вид, приведенный на рис. 1.34.

Рис. 1.34
Теперь произведем замену параллельно соединенного участка из двух резистивных элементов  и
и  эквивалентным сопротивлением величиной
эквивалентным сопротивлением величиной  . Схема цепи после данной эквивалентной замены изображена на рис. 1.35.
. Схема цепи после данной эквивалентной замены изображена на рис. 1.35.

Рис. 1.35
Далее параллельно соединенные ветви из резистивных элементов  и
и  заменим еще одним эквивалентным сопротивлением
заменим еще одним эквивалентным сопротивлением  . Схема цепи после данной эквивалентной замены приведена на рис. 1.36.
. Схема цепи после данной эквивалентной замены приведена на рис. 1.36.

Рис. 1.36
И еще раз произведем эквивалентную замену источников тока с задающими токами  и
и  и внутренними сопротивлениями
и внутренними сопротивлениями  и
и 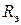 на источники ЭДС с задающими напряжениями
на источники ЭДС с задающими напряжениями  и
и  . Схема замещения рассматриваемой цепи изображена на рис. 1.37.
. Схема замещения рассматриваемой цепи изображена на рис. 1.37.

Рис. 1.37
Итак, в результате всех произведенных эквивалентных преобразований получена одноконтурная цепь, в которой функционирует два источника ЭДС. Теперь представим данные источники одним источником постоянной ЭДС с задающим напряжением  . Окончательно, схема замещения цепи представлена на рис. 1.38.
. Окончательно, схема замещения цепи представлена на рис. 1.38.

Рис. 1.38
Применяя к рассматриваемой цепи второй закон Кирхгофа и закон Ома, получаем следующее решение относительно искомой реакции:


Существует еще один метод эквивалентного преобразования цепи, который удобно применять в случае, когда реакция цепи представляет собой напряжение или ток какой-либо ветви. Данный метод называется методом эквивалентного генератора. Рассмотрим применение этого метода к анализу цепи (рис. 1.39, а).
Пример 5
Пусть в постановке задачи необходимо найти реакцию в виде тока  в рассматриваемой цепи.
в рассматриваемой цепи.

Рис.1.39
В соответствии с данным методом необходимо часть цепи, которая содержит независимые источники электрической энергии, а также другие ветви по отношению к ветви, реакцию на которой нужно найти, представить как активный двухполюсник (рис. 1.39, б). Далее данный активный двухполюсник можно заменить эквивалентным генератором напряжения (теорема Тевенина) с задающим напряжение  и внутренним сопротивлением
и внутренним сопротивлением 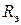 (рис. 1.39, в). Напряжение
(рис. 1.39, в). Напряжение  определяется как напряжение на разомкнутых зажимах
определяется как напряжение на разомкнутых зажимах 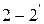 активного двухполюсника (рис. 1.39, г), а внутреннее сопротивление определяется со стороны зажимов
активного двухполюсника (рис. 1.39, г), а внутреннее сопротивление определяется со стороны зажимов 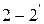 при погашенных независимых источниках (рис. 1.39, д). Гашение источника ЭДС эквивалентно короткому замыканию участка электрической цепи между его зажимами, а гашение источника тока – разрыву.
при погашенных независимых источниках (рис. 1.39, д). Гашение источника ЭДС эквивалентно короткому замыканию участка электрической цепи между его зажимами, а гашение источника тока – разрыву.
|
|
|
Искомый ток  при известных величинах
при известных величинах  и
и 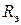 можно отыскать, применяя закон Ома для участка цепи в виде последовательного соединения резистивных элементов
можно отыскать, применяя закон Ома для участка цепи в виде последовательного соединения резистивных элементов 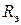 и
и  (рис. 1.39, в), в виде:
(рис. 1.39, в), в виде:
 . (1.44)
. (1.44)
Итак, определим задающее напряжение эквивалентного генератора, проанализировав работу цепи (рис. 1.39, г). Напряжение на зажимах 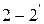 складывается из напряжений на резистивных элементах
складывается из напряжений на резистивных элементах  и
и  .
.
Так как рассматриваемая цепь есть последовательное соединение резистивных элементов, то ток в такой цепи определяется в соответствии с выражением:
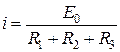 .
.
Тогда задающее напряжение эквивалентного генератора можно определить как
 . (1.45)
. (1.45)
Далее в соответствии с рис. 1.39, д определим эквивалентное сопротивление 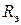 . Сопротивления
. Сопротивления  и
и  соединены последовательно и могут быть заменены на общее сопротивление
соединены последовательно и могут быть заменены на общее сопротивление  . Схема замещения данного участка цепи после эквивалентной замены имеет вид, приведенный на рис. 1.40.
. Схема замещения данного участка цепи после эквивалентной замены имеет вид, приведенный на рис. 1.40.
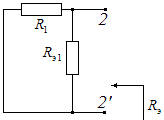
Рис. 1.40
Цепь, приведенная на данном рисунке, представлена параллельным соединением двух ветвей, непосредственно связывающих пару зажимов 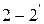 . Тогда эквивалентное сопротивление данного участка цепи определено выражением вида:
. Тогда эквивалентное сопротивление данного участка цепи определено выражением вида:
 . (1.46)
. (1.46)
Подставляя полученные выражения (1.45) и (1.46) в (1.44) получаем искомое решение:
 . (1.47)
. (1.47)
Аналогично рассмотренному примеру, в котором нашла применение теорема Тевенина, активный двухполюсник может быть заменен эквивалентным генератором тока (теорема Нортона) (рис. 1.41) с той лишь разницей, что задающий ток эквивалентного генератора тока  определяется как ток, протекающий через замкнутые накоротко зажимы
определяется как ток, протекающий через замкнутые накоротко зажимы 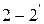 анализируемой цепи. Как следует из рис. 1.41, г, сопротивления
анализируемой цепи. Как следует из рис. 1.41, г, сопротивления  и
и  оказываются шунтированными коротко замкнутым отрезком провода. Тогда задающий ток эквивалентного генератора тока будут определен в виде:
оказываются шунтированными коротко замкнутым отрезком провода. Тогда задающий ток эквивалентного генератора тока будут определен в виде:
 . (1.48)
. (1.48)

Рис.1.41
Что касается внутреннего сопротивления рассматриваемого генератора, то оно определяется также как и в предыдущем случае и равно:
 . (1.49)
. (1.49)
Проанализируем работу цепи, изображенной на рис. 1.41, в для отыскания искомой реакции. Составим систему уравнений электрического равновесия по первому и второму законам Кирхгофа.

Применим во втором уравнении системы закон Ома и решим ее относительно неизвестного тока 

 ;
;  ;
;
 . (1.50)
. (1.50)
Подставляя выражения (1.48) и (1.49) в выражение (1.50) получаем окончательное решение в виде:
 .
.
(1.51)
Сравнив полученные выражения (1.47) и (1.51), можно сделать вывод, что применение теорем Тевенина и Нортона для анализа линейных цепей дают один и тот же результат.
|
|
|


