 |
Внецентренное растяжение-сжатие. Ядро сечения.
|
|
|
|
Понятие сложного сопротивления. Принцип суперпозиции.
Понятие сложное сопротивление означает, что в поперечном сечении бруса под действием его силы возникает более одного внутреннего силового фактора. (простое сопротивление – один силовой фактор).
| Простое сопротивление | Сложное сопротивление |
| 1.Растяжение – сжатие (N) | 1.Поперечный изгиб (Qy,Mx или Qx,My) |
| 2.Кручение (Mz) | 2.Внецентренное растяжение-сжатие (N, Mx, My) |
| 3.Чистый изгиб (Mx или My) | 3.Косой изгиб (Mx, My) |
| 4.Изгиб + кручение (Mизг, Mкр) | |
| 5.Изгиб + растяжение-сжатие (Mизг+N) | |
| 6.Растяжение-сжатие+кручение (N,Mz) |
Принцип суперпозиции (принцип независимости действия сил) означает, что результирующее напряжение в случае сложного сопротивления определяется как сумма напряжений от каждого внутреннего силового фактора в отдельности.
Понятие сложного сопротивления не эквивалентно по смыслу понятию сложного напряженного состоянию (одно не подразумевает другое).
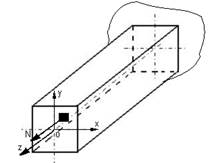а) внецентренное растяжение-сжатие
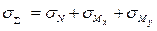
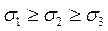
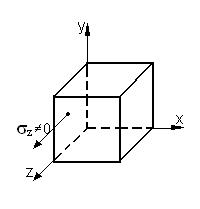
sx=0; sy=0;
txy=0;
tyz=0;
tzx=0;
s1= sz;
s2=0; s3=0
Одноосное напряженное состояние, но сложное сопротивление, т.к. 3 внутренних силовых фактора;
б) кручение
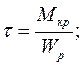
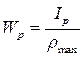
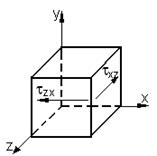
sx=0; sy=0; sz=0
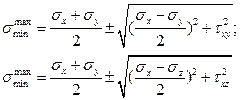
smax = txz;
smin = -txz;
s1 = txz;
s2 = 0;
s3 = -txz
Косой изгиб.
Изгиб называется косым, если плоскость действия возникающим изгибающим моментом, возникающая в поперечном сечении бруса неперпендикулярно ни одной из главных центральных осей сечения.
| Плоский косой изгиб | Пространственный косой изгиб |
| При плоском изгибе упругое линия бруса – это плоская кривая. | При пространственном косом изгибе нагрузки, вызывающие его действуют в разных силовых (продольных) плоскостей. При пространственном косом изгибе упругая линия бруса – это пространственная кривая. |
|
|
|
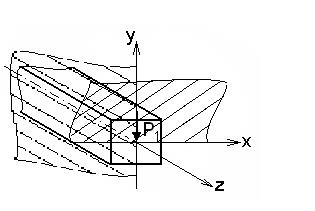
Разложение косого изгиба на две составляющие
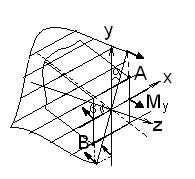
Ф-ла для определения напряжения при косом изгибе.
Координаты x,y принадлежат любой точке поперечного сечения бруса и при определении напряжения следует учитывать их знак.
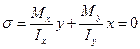
Приравняем данное уравнение к 0 и получим из него уравнение нейтральной линии.
- уравнение нейтральной линии
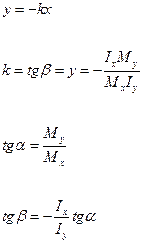
Данная зависимость показывает, что нейтральная линия неперпендиеклярно следу силовой плоскости от момента M.
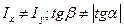- справедливо относится к несимметричному сечению.
В случае симметричного сечения относительно обоих осей (x,y)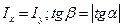 
=>
Нейтральная линия перпендикулярно следу силовой плоскости от момента M.
В точках A и B от действия момента M (возникает максимальное напряжение), тогда условие прочности имеет вид:
Внецентренное растяжение-сжатие. Ядро сечения.
Внецентренное растяжение-сжатие возникает, когда точка приложения нормальной продольной силы смещена от центра тяжести.
Расстояние от центра тяжести сечения до точки придлжения внецентренной нормальной силы называется эксцентриситетом.
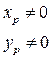
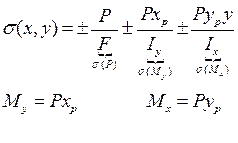
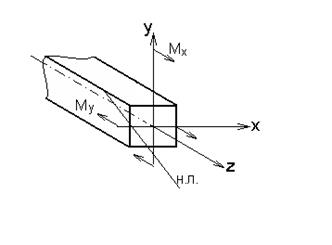
Знак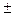 
перед каждым слагаемом принадлежит направлению действия силы.
Приравняем данное уравнение к 0 и получим из него уравнение нейтральной линии.
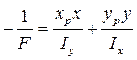
Радиус инерции
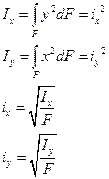
радиусы инерции сечения
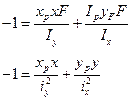
Найдем отрезки xн и yн, отсекаемые нейтральными линиями от оси x и y
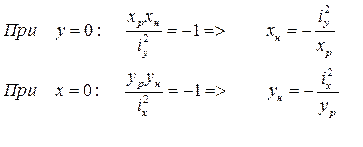
Из полученных формул следует, что нейтральная линия пересекает координаты оси в точках принадлежащих квадрату противоположному тому, в которых приложена внецентренная сила P.
Нейтральная линия в большинстве случаев разделяет сечения на положительные и отрицательные областям напряжениям.
|
|
|
Нормальное напряжение возникает в точках сечения наиболее отдаленной от нейтральной линии.
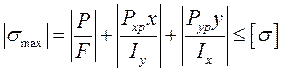
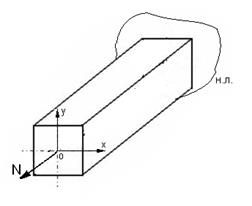
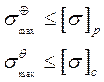
Область вокруг центра тяжести сечения, внутри которой приложения нормальных сил вызывает во всех точках сечения напряжение одного знака называется ядром сечения.
Для определения координаты ядра сечения дадут различные положения нейтральной линии, доводя её касательно к контуру сечения и нигде не пересекая её.
Таким образом определяют координаты соответствующих точек приложения нормальной внецентренной силы по формулам:
-Прямоугольное сечение
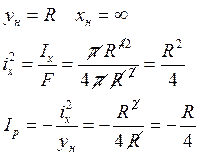
-круглое сечение
|
|
|
