 |
Метод непосредственного интегрирования дифференциального уравнения упругой линии балки.
|
|
|
|
Для получения дифференциального уравнения изогнутой оси уравнения прогибов и уравнения для поворота сечения необходимо провести интегрированные уравнения
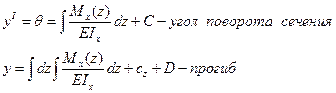
C, D – постоянные интегрирования.
Граничные условия записываются по условию закрепления.
Для консольных балке в заделке y=0, θ=0;
Для балок в опорах y=0
Если балка имеет более одного участка нагружения, то при интегрировании на каждом из них возникает 2 постоянные (C,D), которых находят из граничных условий и условий сопряженных соседних участках.
Пример 1.
Max прогиб возникает в точке приложения силы и обозначения f, данный метод имеет ограниченное применение из-за неудобства нахождения const, если в балке более одного участка нагружения. На каждом участке свои const C и D.
Помимо граничных условий требуется записывать условие сопряжения по соседним участкам.
Пример 2
Метод начальных параметров.
а) M1; M2;… Mn
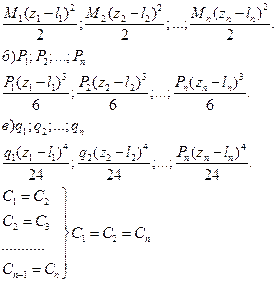
При принятом порядке интегрирования, при условии, что все координаты отсчитываются от общего начало координат, const C и D будут на всех участках одинаковы и могут быть заменены через увеличенные в EIx раз прогиб y0 и угол поворота θ0 в начале координат.
y0,θ0 - начальные параметры представляют собой перемещения в начальных координатах.
а) тогда общее уравнение упругой линии балки выглядит так:
б) уравнение погиба
Потенциальная энергия упругой деформации стержня в общемм случае нагружения.
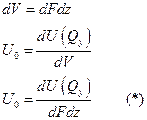
- безразмерные величины, характеризует сечение (геометрию сечения).
|
|
|
А) прямоугольное сечение: 
;
Б) сплошное круглое сечение: 
;
В) для тонкостенного круглого профиля (труба): 
.
 |
Формула справедлива, когда жесткость стержней постоянна.
Теорема Бетти. Теорема Максвелла.
А) 
- прогиб (линейное перемещение);
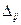- i – показывает направление перемещения от действия силы;
j – номер силы, вызвавшей это перемещение.
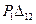- работа силы 
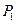на перемещении 
по ее направлению от действия силы 
. Т.к. 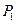к моменту начала действия силы уже исчерпана и остается постоянной по величине, то перед этим слагаемым нет коэффициента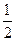 
.
Б)
Приравняем (*) и (**):
Теорема Бетти – теорема о взаимности работ.
 |
Работа I силы на перемещении по её направлению от действия II силы равна работе II силы на перемещении по ее направлению от действия I силы.
Если P1 и P2 – единичные силы.
Перемещение точки приложения точка P1 в направлении ее действии, вызвавшее силой P2 равно перемещению точки приложения; точка P2 в направлении ее действии, вызвавшее действительные силы P2.
Теорема Кастилиано.
- энергия, накопленная в результате деформации системы только силами Q и численно равная работе сил Q на вызванных ими перемещениях.
Так как частное произведение от потенциала энергии деформации, взятая по одной из внешних сил равно перемещению точки приложения этой силы в направлении ее действия.
Если частное произведение берется по силе - получается прогиб, если по моменту – угол поворота сечения.
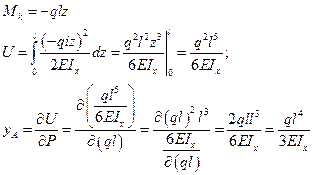
Интеграл Мора.
Примем следующие нагружения балки. Сначала приложим силу P1, затем нагрузим. Определим работу постоянной по величине единичной силы на перемещении по направлению её действия от заданной нагрузки.
Правило Верещагина.
Правило Верещагина – графическое выражение интеграла Мора, применимо для стержней с прямолинейной осью. При приложении единичной нагрузки к прямолинейной оси, единичная эпюра всегда линейна (треугольник или прямоугольник).
|
|
|
Глава 11.
Статически неопределимые системы.
|
|
|
