 |
Применение методов дифференциального исчисления при решении прикладных задач.
|
|
|
|
Задача 8.
Проектируется канал оросительной системы с прямоугольным сечением в 4,5 м2. Каковы должны быть размеры сечения, чтобы для облицовки стенок и дна пошло наименьшее количество материала?
Решение.
Пусть стенки канала имеют длину x м., а дно канала – y м.
Тогда:
 |
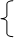x*y=4,5 y=4,5/x
S= L*(2x+y) S=L*(2x+4,5/x)
Найдем производную.
Так как S’=0, и L(длина канала)-положительное число,то
x=1,5 Легко убедиться, что при данном x значение S минимально
Ответ: x=1,5 м. y=3 м.
Задача 9.
Какова должна быть скорость парохода,чтобы общая сумма расходов на один км. пути была наименьшей, если расходы на топливо за один час пропорциональна квадрату скорости.
Решение.
Расходы на 1км пути на эксплуатацию парохода состоят из расходов на топливо и других расходов (содержание команды, амортизация). Ясно, что чем быстрее движется пароход, тем больше расход топлива. Остальные расходы от скорости движения не зависят.
Обозначим через S-сумму расходов в час, V- скорость судна
Расходы на 1км выразится формулой S/V
По условию имеем S=KV2+b, где K- коэффициент пропорциональности, b- расходы, кроме расходов на топливо.
Y=S/V Y=(KV2+b)/V=KV+b/V
Надо найти значение V, при котором функция Y=KV+b/V имеет наименьшее значение.
Y¢=K=b/V2 Y¢=0
V=Öb/V
Таким образом общая сумма расходов на 1 км. пути будет наименьшей при V=Öb/V.
Значение коэффициентов b и K определяются из опыта эксплуатации парохода.
Задача 10.
Над центром круглого стола радиусом r висит лампа. На какой высоте h следует повесить эту лампу, чтобы на краях стола получить наибольшую освещенность?
|
|
|
Из физики известна формула E=k*sinj/(h2+r2)
sinj=h/Ö(h2+r2)
Для упрощения решения задачи вместо функции
E=k*sinj/(h2+r2)=k*h/(h2+r2)3/2 возьмем функцию
T=1/k2*E2=h2/(h2+r2), для упрощения формулы заменим
h2=z
тогда:
T=z/(z+r2)3
T¢= ((z+r2)3-z*3*(z+r2)2)/ (z+r2)6=(z+r2-3*r)/ ((z+r2)4
T¢=0® r2-2*r=0® z=r2/2 h=r/Ö2
Ответ. Освещенность максимальная, если h=r/Ö2
Задача 11.
Нахождение гидравлически наиболее выгодного трапециидального сечения русла.
Из всех сечений русла, представляющих собою равнобедренную трапецию, имеющих одинаковую площадь w и уклон i, найти то, которое будет пропускать наибольший расход Q.
Пояснение:
1. Расход Q –это количество воды, проходящее через поперечное сечение русла в единицу времени
2. Расход Q определяется по формуле: Q=w*cÖr*j
w-площадьсечения
c-коэффициент
r-гидравлический радиус
i -уклон дна русла
3. Гидравлический радиус есть отношение площади сечения к смоченному периметру c: r=w/c
4. Смоченный периметр есть линия соприкосновения жидкости с поверхностью канала.
5. Крутизна 1/m откоса есть отношение высоты откоса к заложению (АО).
Решение. Расход Q зависит от r, и он будет наибольшим при rmax, что будет тогда, когдаcmin
Крутизна откоса 1/m =h/АО, то АО=h*m
Тогда w=1/2*(b+2*m*h+b)h=(b+m*h)*h
c=b+2*hÖ1+m2т.е.
c=(w/h-m*h)+2*hÖ1+m2
c(h)=(- w/h2-m)+2Ö1+m2
c(h)=-(b+m*h)/h-m+2Ö1+m2
c(h)=-b/h+2(Ö(1+m2)-m) c(h)=0 при b/h=2(Ö(1+m2)-m)
c(h)¢¢>0 при h=b/2(Ö(1+m2)-m)
Ответ. c имеет наименьшее значение при условии h=b/2(Ö(1+m2)-m)
Заключение.
В настоящее время получило всеобщее признание то, что успех развития многих областей науки и техники существенно зависит от развития многих направлений математики. Математика становится средством решения проблем организации производства, поисков оптимальных решений и, в конечном счете, содействует повышению производительности труда и устойчивому поступательному развитию народного хозяйства.
|
|
|
Использование экстремальных задач при изучении математики оправдано тем, что они с достаточной полнотой закладывают понимание того, как человек ищет, постоянно добивается решения жизненных задач, чтобы получающиеся результаты его деятельности были как можно лучше. Решая задачи указанного типа, наблюдаем, с одной стороны, абстрактный характер математических понятий, а с другой – большую эффективную их применимость к решению жизненных практических задач.
Экстремальные задачи помогают ознакомиться с некоторыми идеями и прикладными методами школьного курса математики, которые часто применяются в трудовой деятельности, в познании окружающей действительности.
Решение экстремальных задач способствует углублению и обогащению наших математических знаний. Через задачи мы знакомимся с экстремальными свойствами изучаемых функций, с некоторыми свойствами неравенств. Эти задачи могут серьезно повлиять на содержание учебного материала, на аспекты применения положений изучаемой теории на практике.
Список литературы
1. Башмаков М. И. Алгебра и начала анализа 10-11. М.: Просвещение, 1992.
2. Беляева Э. С., Монахов В.М. Экстремальные задачи. М.: Просвещение, 1997.
3. Виленкин Н. Л. Функции в природе и технике. – М.: Просвещение, 1978
4. Возняк Г. М., Гусев В. А. Прикладные задачи на экстремумы. М.: Просвещение, 1985.
5. Гейн А. Г. Земля Информатика. – Екатеринбург: Издательство Уральского университета, 1997
6. Гнеденко Б. В. Введение в специальность математика. – М: Наука, 1991
7. Гнеденко Б. В. Математика в современном мире. М: Просвещение, 1980.
8. Перельман Я. И. Занимательная алгебра. М: АО “Столетие”, 1994
9. Хургин Я. И. Ну и что? (Разговоры математика с биологами и радистами, врачами и технологами… о математике и ее связях с другими науками). М.: Молодая гвардия, 1967.
10. Шибасов Л. П., Шибасова З. Ф. За страницами учебника математики. – М.: Просвещение, 1997
|
|
|
