Теорема о разложении определителя по элементам строки или столбца

Определитель матрицы. Вычисление определителей второго и третьего порядков

Пусть дана квадратная матрица второго порядка:

 

Определителем (или детерминантом) второго порядка, соот твующим данной матрице, называется число

 

Определитель второго порядка записывается так:

Отметим, что определитель второго порядка равен разности попарных произведений элементов главной и побочной диагоналей.

26. Вычислить определители второго порядка:

27—32. Вычислить определители:

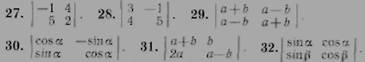
Пусть дана квадратная матрица третьего порядка:

Определителем (или детерминантом) третьего порядка, соответствующим дайной матрице, называется число

Определитель третьего порядка записывается так:

При вычислении определителей третьего порядка удобно пользоваться правилом треугольников (правилом Сарруса). Это правило проиллюстрируем на схеме:

Три положительных члена определителя представляют собой произведения элементов главной диагонали и элементов, находящихся в вершинах двух равнобедренных треугольников основания которых параллельны главной диагонали (а₁₂а₂₃а₃₁ и а₂₁а₃₂а₁₃). Три отрицательных его члена есть произведение элементов побочной диагонали и элементов, находящихся в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали ( и а₁₁а₂₃а₃₂)

33. Вычислить определители третьего порядка:

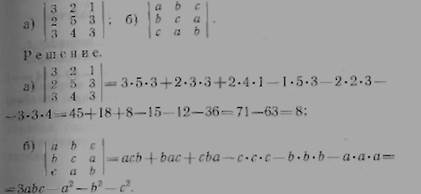
34—39. Вычислить определители:

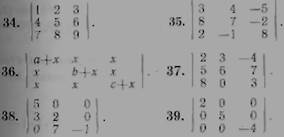
Основные свойства определителей

1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами (т. е. транспонировать):

Например,

Это свойство называют свойством равноправности строк и столбцов.

2. При перестановке двух строк (или столбцов) определитель изменит свой знак на противоположный:

Например,

Поменяв местами первый и второй столбцы, получим

3. Общий множитель всех элементов строки (или столбца) можно вынести за знак определителя:

Например,

Если множитель (—2) вынести за знак определителя, то по­лучим

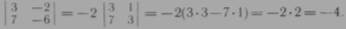
4. Определитель с двумя одинаковыми строками или столб­цами равен нулю.

Например,

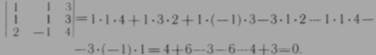
Из свойств 3 и 4 вытекает следующее свойство:

5. Пели все элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю.

Например,

6. Если к какой-либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столо-

ца) умноженные на одно и то же число, то определитель не изменит своей величины:

7. Треугольный определитель, у которого все элементы, лежащие выше (или ниже) главной диагонали, — нули, равен произ­ведению элементов главной диагонали:

Миноры и алгебраические дополнения элементов определителя

Минором элемента определителя не и меняются от 1 до п, называется такой новый определитель, который получается из данного определителя вычеркиванием строки и столбца, содержащих данный элемент.

Например, минор , соответствующий элементу опреде­лителя

получается, если вычеркнуть из определителя D первую строку и второй столбец, т. е.

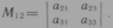
40. Записать все миноры определителя

41. Записать все миноры определителя

Алгебраическим дополнением элемента определителя D

называется минор этого элемента, взятый со знаком .Алгебраическое дополнение элемента принято обозначать .

Таким образом,

42. Найти алгебраические дополнения элементов определителя

43. Найти алгебраические дополнения элементов
определителя

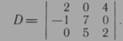
Теорема о разложении определителя по элементам строки или столбца

Сумма произведений элементов любой строки (или столбца) определителя D на их алгебраические дополнения равна этому определителю, т. е.

или

Эти соотношения называются разложением определителя по эле­ментам i-й строки или j-го столбца.

44. Определитель

разложить: а) по элементам 1-й строки; б) по элементам 2-го столбца.

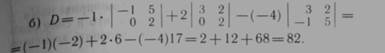
Если определитель имеет четвертый или более высокий поря-то его также можно разложить по элементам строки или столбца а затем понижать порядок алгебраических дополнений.

45. Вычислить определитель

Решение. Разложим определитель по элементам 1-й стро­ки (так как она содержит два нулевых элемента):

Поскольку второй и четвертый члены разложения равны нулю, имеем

46—48. Вычислить определители третьего порядка:

51. Вычислить определители четвертого порядка:

Перечислим различные способы вычисления определителей.

1. Определитель можно вычислить, используя непосредственно его определение. Этим способом удобно находить определители второго и третьего порядков, а для определителя более высокого порядка применим следующий способ.

2. Определитель можно вычислить с помощью его разложения по элементам строки или столбца.

3. Определитель можно вычислить способом приведения к треугольному виду. Этот способ основан на том, что в силу свойства 7 треугольный определитель равен произведению элементов 1 главной диагонали.

Чтобы получить треугольный определитель, нужно, используя свойство 6, к какой-либо строке (или столбцу) заданного определителя прибавлять соответствующие элементы другой строки 1 (или столбца), умноженные на одно и то же число, до тех пор пока не придем к определителю треугольного вида.

Пусть, например, требуется вычислить определитель

Вычитая первую строку из всех остальных, сразу получим определитель треугольного вида:

§ 3. Обратная матрица. Обращение матриц второго! и третьего порядков

• I. Определение обратной матрицы

• 2. Вычисление обратных матриц второго и третьего порядков

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: