 |
Применение формул Крамера к решению систем линейных уравнений
|
|
|
|
Рассмотрим применение формул Крамера к решению систем двух линейных уравнений с двумя неизвестными.
71. Решить систему уравнений
Итак, решение системы есть (3; —1).
72. Решить систему уравнений
Так как 
, а 
, то система не имеет решений
(уравнения противоречивы).
73. Решить систему уравнений
Данная система имеет бесчисленное множество решение! (коэффициенты при неизвестных пропорциональны). 74. Решить систему уравнений
Решение. Вычислим определитель системы и определители при неизвестных:
Найдем значения х, у, г по формулам Крамера:
Итак, получаем ответ: (1; 1; 2).
75—81. Решить по формулам Крамера следующие системы уравнений:
& 6. Решение систем линейных уравнений методом Гаусса
При решении систем линейных уравнений используют также год Гаусса (метод последовательного исключения неизвестных) Он состоит в следующем: систему уравнений приводят к эквивалентной, если системе с треугольной матрицей (системы называются эквивалентными, если множества их решений совпадают). Эти действия называют прямым ходом. Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).
При выполнении прямого хода используют следующие преобразования:
1) умножение или деление коэффициентов свободных членов на одно и то же число;
2) сложение и вычитание уравнений:
3) перестановку уравнений системы;
4) исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю.
82. Используя метод Гаусса, решить систему уравнений
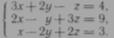
Решение. Переставим третье уравнение на место первого:
Запишем расширенную матрицу:
Чтобы в 1-м столбце получить 
, умножим 1-ю строку сначала на 3, а затем на 2 и вычтем результаты из 2-й и 3-й строк:
|
|
|
Разделим 2-ю строку на 8, полученные результаты умножим на 3 и вычтем из 3-й строки:
Запишем новую эквивалентную систему, которой соответствует расширенная матрица:
Выполняя обратный ход, с помощью последовательных подстановок находим неизвестные:
Итак, получаем ответ: (1; 2; 3).
83. Решить методом Гаусса систему линейных уравнений
Решение. Составим расширенную матрицу системы:
Последовательно умножим 1-ю строку на 3 и 2 и вычтем результаты из 2-й и 3-й строк, а из 4-й строки вычтем 1-ю:
Вычтем 2-ю строку последовательно из 3-й и 4-й:
Отбросив нулевые строки, получим матрицу
Разделим вторую строку на 5:
Эта расширенная матрица соответствует системе уравнений
мы знаем, что система двух уравнений с четырьмя неизвестными имеет бесчисленное множество решений. 04—89.Решить метолом Гаусса следующие системы уравнений:
Вопросы и задачи для конспектирования
1. Что называется матрицей?
2. Что называется матрицей-строкой? матрицей-столбцом? вектором?
3. Какие матрицы называются прямоугольными? квадратными?
4. Какие матрицы называются равными?
5. Что называется главной диагональю матрицы?
6. Какая матрица называется диагональной?
7. Какая матрица называется единичной?
8. Какая матрица называется треугольной?
9. Что значит «транспонировать» матрицу?
10. Транспонируйте матрицу
11. Что называется суммой матриц?
12. Сложите матрицы?
13. Чтоназывается произведением матрицы на число?
14. Как найти произведение двух матриц?
15. В нем состоит обязательное условие существования произведения матриц?
16. Найдите произведение матриц:
17. Какими свойствами обладает произведение матриц?
18. Что называется определителем матрицы?
19. Как вычислить определитель третьего порядка по схеме треугольников?
|
|
|
20.Что называется минором?
21.Что называется алгебраическом дополнением элемента определителя?
22.Как разложить определитель по элементам столбца или строки?
23.Какие способы вычисления определителя вам известны?
24.Перечислите свойства определителей.
25.Какая матрица называется невырожденной?
26.Какая матрица называется обратной но отношению к данной?
27.Каков порядок вычисления обратной матрицы?
28.Вычислите обратную матрицу для А = 
.
29.Как записать простейшее матричное уравнение?
30.Как решить матричное уравнение?
31.Решите матричным способом систему уравнений
32. Сформулируйте теорему Крамера.
33- Запишите формулы Крамера.
34. Решите но формулам Крамера систему уравнений из задачи 31.
35.Опишите метод Гаусса.
36.Решите методом Гаусса систему уравнений из задачи 31.
Контрольное задание
4 решите методом Гаусса систему уравнений
Вариант 2
1. Вычислите А' — 2В, если
2. Решите матричным способом систему уравнений
3. Решите по формулам Крамера систему уравнений
4. Решите метолом Гаусса систему уравнений
|
|
|
