Схемы замещения электрических сетей

Натуральная мощность и пропускная

Способность ЛЭП

Натуральная мощность

 

Рассмотрим ЛЭП без потерь, для которой r ₀ = 0 и g ₀ = 0.

Выделим в ней отрезок единичной длины D l с индуктивным сопротивлением x ₀D l и емкостной проводимостью b ₀D l. На этом участке имеют место потери и генерация реактивной мощности

(2.39)

Здесь Q_C не зависит от передаваемой мощности. Если принять Q = 0, то при некоторой активной мощности P будет иметь место равенство Q_L = Q_C. Мощность, передаваемую в этом режиме называют натуральной мощностью P _нат, а сам режим работы ЛЭП называют режимом передачи натуральной мощности. При U = U _ном будем иметь

(2.40)

и

, (2.41)

откуда

(2.42)

или

(2.43)

где – волновое сопротивление линии.

В реальной линии, в которой r ₀ ¹ 0 g ₀ ¹ 0, потери активной мощности при Q = 0 будут наименьшими

(2.44)

а при P = P _нат линия будет работать с наибольшим КПД вследствие того, что линия находится на самобалансе реактивной мощности Q_L = Q_C – потери в линии компенсируются зарядной мощностью и в любой точке линии Q = 0.
В случае, когда Q_L ¹ Q_C имеет место либо избыток зарядной мощности
Q_C > Q_L, либо потери превышают зарядную мощность Q_L > Q_C, и тогда потери D P увеличиваются и вследствие этого КПД линии ухудшается, как при
P > P _нат, так и при P < P _нат.

Режим натуральной мощности является не только самым экономичным. Для линии без потерь можно обнаружить и другие его замечательные свойства, так, например, напряжение в начале линии по модулю оказывается равным напряжению в конце линии:

(2.45)

где ; Z_C – волновое сопротивление линии; b₀ – коэффициент фазы линии, а U ₂ – совмещено с действительной осью координат.

Из соотношения следует, что равны по модулю не только напряжения по концам линии, но и то, что модуль напряжения в любой точке вдоль линии является неизменной величиной: , где x – расстояние от начала линии (x = 0) до точки с координатой x. Можно показать, что для линии без потерь в режиме натуральной мощности и ток вдоль линии по модулю остается постоянной величиной.

Такое свойство постоянства напряжения и тока вдоль линии в режиме натуральной мощности во многом снижает требования к оборудованию линии электропередачи и облегчает регулирование режимов ЭЭС.

Наличие активных параметров линии r ₀ и g ₀ несколько меняет идеальную картину, но при P ₂ = P _нат или P ₂, близкой к натуральной, в линии приблизительно сохраняются свойства режима натуральной мощности.

В табл. 2.1 приведены численные значения натуральной мощности ВЛ некоторых напряжений. Натуральные мощности кабельных линий на порядок выше, чем у ВЛ.

Т а б л и ц а 2.1

Величины натуральной и наибольшей

передаваемой мощности ВЛ

 

Мощность	Номинальное напряжение, кВ
Натуральная
Наибольшая*	20…50	90…200	700…900

 

* Наибольшая мощность зависит от длины линии.

 

На практике невозможно обеспечить работу всех линий в режиме, близком к натуральному, но этого добиваются для отдельных линий, когда существует возможность регулировать передаваемую мощность за счет перераспределения мощностей в электрической сети и генерирования реактивной мощности в местах ее потребления.

 

Пропускная способность

 

Пропускная способность ЛЭП определяется величиной активной мощности, которую линия может передать при выполнении всех условий, от которых зависит ее нормальная работа.

Вновь рассмотрим линию без потерь, но представленную только ее индуктивным сопротивлением (рис 2.9, а, б).

 

б

а

Рис. 2.9. Схемы замещения линии без потерь: а – с емкост-

ными проводимостями; б – зарядные токи включены в токи

по концам линии

Такое представление не является допущением, так как емкостные токи по концам схемы (рис. 2.9, а) входят в токи I ₁ и I ₂ для схемы (рис. 2.9, б), соответственно имеем I ₁ = I ₂ = I.

Построим векторную диаграмму линии.

Рис. 2.10. Векторная диаграмма линии без потерь

 

На векторной диаграмме (рис. 2.10), вектор падения напряжения D U будет

. (2.46)

Спроектируем на мнимую ось векторы U ₁ и D U, получим соотношение

. (2.47)

Умножим обе части этого выражения на U ₂, будем иметь

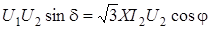. (2.48)

В полученном выражении есть активная мощность в конце линии P ₂. После преобразования получим

(2.49)

или для линии без потерь P = P _maxsind.

Эта зависимость изображается в виде синусоиды (рис. 2.11).

Максимальная мощность ЛЭП P _max называется пределом передаваемой мощности, который достигается при угле d = 90°. Устойчивая работа генераторов ЭЭС возможна только при d < 90° и на восходящей ветви синусоиды. Точка d = 90° является граничной между областями устойчивой и неустойчивой работы генераторов. Чтобы предотвратить выход генераторов в неустойчивую область, делают некоторый запас по устойчивости, равный примерно 15° от P _max.

 

 

Рис. 2.11. Характеристика мощности ЛЭП

 

По ЛЭП протекает ток , который не может превысить предельно допустимое значение 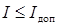, определяемое тепловыми условиями работы проводника. Так, например, голые провода по условию допустимого нагрева нельзя нагревать до температуры более 70°. Значения I _доп приводятся в справочной литературе для каждой марки провода.

Напряжения по концам линии U ₁ и U ₂ имеют технические и режимные ограничения как по минимальному, так и по максимальному значению. Так, например, по условиям работы электрической изоляции ВЛ в России допускается превышение напряжения относительно номинального значения не бо-
лее чем:

· на 20 % при U _ном до 20 кВ;

· 15 % при U _ном = 35 … 220 кВ;

· 10 % при U _ном = 330 кВ;

· 5 % при U _ном = 500 кВ и выше.

Силовые трансформаторы допускают превышение напряжения относительно напряжения рабочего регулировочного ответвления не более чем на 5 %, что вызвано недопустимостью перехода трансформатора в режим работы с нелинейной частью характеристики намагничивания сердечника.

Предельные максимальные и минимальные значения напряжений в ЛЭП обусловлены также условиями регулирования напряжения, а также устойчивостью работы генераторов ЭЭС.

С учетом изложенного выше можно обобщить ограничения на параметры режима ЛЭП на диаграмме мощностей (P, Q) (рис. 2.12).

На диаграмме мощностей принято положение направления мощности от начала к концу ЛЭП по P и Q – первый квадрант.

Рис. 2.12. Диаграмма мощностей ЛЭП

 

Диаграмму можно построить для начала и конца линии.

Из диаграммы (рис.2.12) видно, что пропускная способность ЛЭП зависит от следующих параметров:

· величины передаваемой реактивной мощности;

· предельно допустимого тока по проводам линии;

· предела передаваемой мощности и запаса по устойчивости;

· предельных значений напряжений по концам ЛЭП.

Чтобы получить величину мощности P, которую возможно передать по ЛЭП (оценить пропускную способность ЛЭП), необходимо на диаграмме мощностей отложить требуемую для передачи реактивную мощность Q (в начале или конце линии) и провести отрезок горизонтальной прямой до первого пересечения с кривыми ограничений. Проекция точки пересечения на ось P дает максимально возможное значение передаваемой мощности. Если реактивную мощность в конце линии можно регулировать (управлять ею), то, скорее всего, пропускная способность будет определяться ограничением по I _доп (для ВЛ с U _ном £ 220 кВ) или пределом передаваемой мощности и запасом по устойчивости (для ВЛ с U _ном ³ 330 кВ).

 

Схемы замещения электрических сетей

 

Различают несколько типов схем электрических сетей, таких, как:

· принципиальная схема соединений;

· схема замещения;

· расчетная (преобразованная) схема замещения.

Все схемы трехфазных элементов ЭЭС, как правило, изображаются в однолинейном виде. На рис. 2.13 показаны все три вида схем, состоящих из одной ЛЭП и одного двухобмоточного трансформатора с нагрузкой на стороне низкого напряжения.

 

в

б

а

RЛ + jXЛ

Рис. 2.13. Схемы электрической сети: а – принципиальная схема;

б – схема замещения; в – расчетная схема (сопротивления в омах,

проводимости в микросименсах, мощности в мегавольт-амперах,

коэффициент трансформации в о.е.)

 

Схемой замещения вида, приведенной на рис 2.13, б, удобно пользоваться, когда выполняется одиночный расчет простых схем, как правило, в учебных целях без использования специальных программ. В большинстве случаев при расчетах режимов электрических сетей используется расчетная схема
рис. 2.13, в или подобная ей, где задаются электрические параметры элемен-
тов сети.

Совершенно естественным является удаление из схемы элементов, влияние которых на режим сети является пренебрежимо малым. Так не учитывают:

· потери на корону в ВЛ до 220 кВ;

· зарядную мощность в ЛЭП до 35 кВ, а для коротких ВЛ и 110 кВ;

· потери холостого хода трансформаторов, если не нужно решать вопросы повышения экономичности работы электрических сетей;

· активные сопротивления обмоток трансформаторов, если не нужно оценивать потери электрической энергии и решать вопросы повышения экономичности работы электрических сетей.

В трехобмоточных трансформаторах и автотрансформаторах индуктивное сопротивление обмоток СН принимают равным нулю и при пренебрежении активным сопротивлением получается ветвь с нулевым сопротивлением. В таких случаях можно приблизительно оценить потери реактивной мощности в обмотке НН, сложить эти потери с реактивной мощностью нагрузки НН и добавить полученную мощность на шины СН. Трехлучева схема замещения трансформатора превращается в одну ветвь с сопротивлением обмотки ВН и трансформацией с вн на СН; k _В-С.

Современные программы расчета режимов в энергосистемах вообще не предполагают составления схем замещения или расчетных схем и используют принципиальные схемы, в которых указываются марки (тип) оборудования, число параллельных элементов и расстояния между подстанциями, которые соединяются посредством ЛЭП. Кроме того, все оборудование ЭЭС, нагрузки и варианты схем соединений закладываются в специализированные базы данных, на основе которых ведется формирование схем для расчетов различных режимов.

В тех случаях, когда необходимо составить схему замещения сети с параллельными элементами (2 цепи ЛЭП, 2 трансформатора и т. п.) или упростить расчетную схему, выполняются последовательно-параллельные преобразования схем. В некоторых случаях выполняются преобразования треугольника в звезду и наоборот.

Отдельные энергосистемы соединяются между собой и образуют объединения энергосистем и единую энергосистему страны. Расчеты установившихся режимов таких больших схем проводятся крайне редко, но при выполнении расчетов режимов отдельных энергосистем следует учитывать влияние их соседних энергосистем.

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: