 |
В радиально-магистральных сетях
|
|
|
|
Магистралью называется линия с промежуточными отборами мощности вдоль линии (рис. 2.14, а). В пределе с увеличением числа нагрузок получается линия с равномерно распределенной нагрузкой (рис. 2.14, б), где плотность нагрузки на единицу длины одинакова для любого участка.
|
|
|
|
Рис. 2.14. Виды схем: а – магистраль; б – линия с равно-
мерно распределенной нагрузкой; в – радиальная схема;
г – радиально-магистральная схема
Радиальные линии исходят из одной точки сети (рис. 2.14, в).
Радиально-магистральные линии включают в себя элементы магистральной и радиальной линий (рис. 2.14, г).
Приближенное распределение потоков мощностей в магистральной линии можно определить с помощью линии сечения.
Сечением будем называть замкнутую линию, которая пересекает только один участок линии и не включает источник питания – точку, откуда исходит магистраль.
Поток мощности по j -му участку равен сумме мощностей нагрузок, охватываемых линией сечения
, (2.50)
где s – множество номеров нагрузок, охваченных сечением j -го участка.
Для схемы магистрали (рис. 2.15) даны три линии сечения, каждая из которых охватывает одну, две или три нагрузки. Соответственно потоки мощности для участков будут определяться как:
· для первого участка – мощность первой нагрузки;
· для второго участка – сумма мощностей первой и второй нагрузок;
· для третьего участка – сумма мощностей всех трех нагрузок.
Рис. 2.15. Сечения участков магистрали
Для радиальной сети поток мощности равен мощности нагрузки, которая подключена к конечному узлу участка:
, (2.51)
так как все сечения охватывают только по одной нагрузке.
Потокораспределение в радиально-магистральных сетях в общем случае определяется линиями сечений по формулам (2.50).
|
|
|
В расчете потокораспределения с учетом потерь мощности и зарядной мощности ЛЭП для каждого участка рассчитываются потоки мощности у начального и конечного узлов 
.
Для расчетов надо использовать правильно выбранную последовательность вычислений на участках сети. Таких последовательностей может быть несколько. Приведем один алгоритм получения последовательности расчетов участков.
Вначале рассчитываются участки, которые являются радиальными: один из узлов, к которому присоединяется рассчитываемая ветвь, является «висячим», к нему подходит только одна ветвь.
Рассчитанные ветви из дальнейшего рассмотрения исключаются.
Затем вновь проверяется, какие участки оказались радиальными после исключения рассчитанных участков. Эти участки рассчитываются и также исключаются из дальнейшего рассмотрения.
Подобная процедура повторяется до тех пор, пока не будут рассчитаны все участки сети. Так заканчивается первый этап расчета – этап расчета потокораспределения.
Второй этап – расчет режима напряжений – ведется в обратном порядке от головных участков к последним, с которых начинался расчет в первом этапе.
Рассмотрим пример (рис. 2.16).
Рис. 2.16. Пример для иллюстрации расчета
радиально-магистральной сети
Сеть состоит из четырех узлов нагрузки и четырех участков. Номера ветвей указывают, в каком порядке будет выполняться их расчет на первом этапе потокораспределения. В потоки мощности на участках включаются не только мощности нагрузок, охваченных соответствующими линиями сечения, но и потери мощности на рассчитанных участках. Таким образом, мощность пункта питания будет равна сумме всех мощностей нагрузок плюс сумма потерь мощности на всех участках сети.
Все мощности в поперечных ветвях схемы замещения сети (зарядная мощность ЛЭП, потери холостого хода трансформаторов, потери на корону) обычно включаются в мощности нагрузки на предварительном этапе формирования расчетной схемы замещения сети.
|
|
|
Пример
Рассчитать потокораспределение в сети, представленной на рис. 2.16. Номинальное напряжение сети – 110 кВ.
Линии 1 и 2 выполнены проводом марки АС 70/11, а линии 3 и 4 – АС 95/16. Все параметры сети и расчет приведен в системе Mathcad.
Параметры линий: сопротивления в омах, проводимости в сименсах. Мощности в мегавольт-амперах, напряжения в киловольтах.
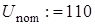
Расчет параметров сети
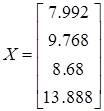
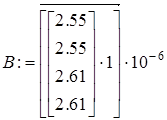
Мощности нагрузок и расчетные мощности (учет зарядных мощностей ЛЭП)
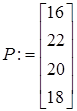
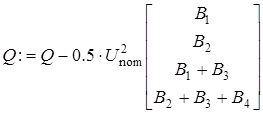
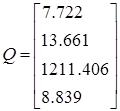
Этап 1. Расчет потоков мощностей. Потоки мощности в начале ветви обозначены индексом 1.
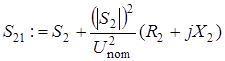
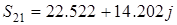
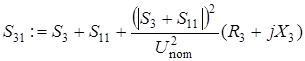
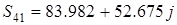
Потери мощности из баланса мощности в сети (учтена зарядная мощность в начале участка 4)
.
Этап 2. Расчет напряжений в узлах
2.8. Распределение мощностей в простейших
замкнутых сетях
Замкнутые сети
Замкнутыми сетями называются сети, имеющие контуры (циклы), образованные ЛЭП и трансформаторами (рис. 2.17).
|
|
Рис. 2.17. Примеры замкнутых схем электрических сетей:
а – сеть одного напряжения; б – сеть двух напряжений
К замкнутым сетям относятся также сети, имеющие несколько источников питания. Одной из таких схем является так называемая линия с двусторонним питанием (рис. 2.18).
Здесь буквами А и Б обозначены пункты питания, питающие нагрузки Н1 и Н2, расположенные вдоль линии.
Рис. 2.18. Линия с двусторонним питанием
Определение потокораспределения в линии
с двусторонним питанием при одинаковых напряжениях
пунктов питания
Найдем потокораспределение в линии с двумя нагрузками (рис. 2.18).
Пусть U А = U Б и d = 0: напряжения равны по модулю и по фазе.
Предварительно на расчетной схеме сети произвольно укажем направления потоков мощности по участкам: S 1, S 2 и S 3 (рис. 2.19), считая пока, что потери мощности на участках равны нулю. Для удобства расчета в мощности нагрузки уже включены зарядные мощности участков линии.
Рис. 2.19. Потоки мощности в линии с двусторонним питанием
Запишем для схемы (рис. 2.19), второй закон Кирхгофа
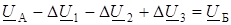. (2.52)
|
|
|
С учетом 
и 
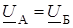получим
. (2.53)
Полагая напряжения в узлах равными номинальному значению, получаем
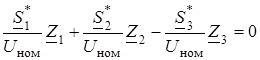(2.54)
или комплексно-сопряженное уравнение
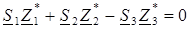. (2.55)
Выразим потоки мощности по второму и третьему участкам линии че-
рез мощность на первом участке и мощности нагрузок: S 2 = S 1 – S Н1 и
S 3 = S Н1 + S Н2 – S 1 и подставим их в (2.55). После некоторых преобразований получим формулы для определения приближенного потокораспределения в линии с двусторонним питанием
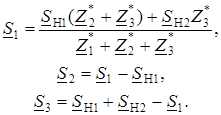(2.56)
Полученная группа выражений (2.56) определяет потокораспределение
в линии с двусторонним питанием без учета потерь мощности.
В одной из точек сети 1 или 2 потоки мощности будут направлены встречно друг другу. Такая точка называется точкой потокораздела в линии (рис. 2.20, а).
Для учета потерь в сети можно сделать расчетный прием – разделение ли-нии с двухсторонним питанием по точке потокораздела на две магистральные линии (рис. 2.20, б): первая (слева) – участки 1 и 2 и, вторая (справа) – участок 3. При этом нагрузка узла 2 в первой схеме будет равна потоку мощности
в конце второго участка S 2(к) = S 2, а во второй схеме – S 3(к) = S 3. Сумма этих потоков мощности равна исходной нагрузке второго узла S 2(к) + S 3(к) = S Н2.
|
|
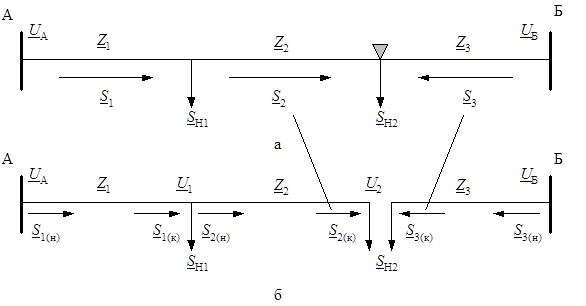
Рис. 2.20. Приведение линии с двусторонним питанием
к двум магистральным линиям
Расчет магистральных схем ведется в обычном порядке:
Этап 1
Первая схема
1)  ;
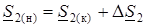2)  ;
3)  .
| Вторая схема
 .
|
Этап 2
Первая схема
1)  ;
2) 
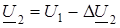
| Вторая схема
|
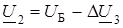
Таким образом, расчет линии с двусторонним питанием требует определения приближенного потокораспределения для отыскания точки потокораздела и затем сводится к расчету двух магистральных схем.
Отметим, что напряжение U 2 можно найти из расчета второй схемы {D U 3, U 2}. Разница в напряжениях во втором узле, найденных по первой и второй схемах, может служить оценкой погрешности расчета.
Определение потокораспределения в линии
с двусторонним питанием при различающихся напряжениях
пунктов питания
Для расчета потокораспределения при различающихся напряжениях пунктов питания А и Б можно воспользоваться методом наложения. Первый расчет выполняется для случая, когда напряжения равны между собой (см. п. 2), а второй – при отсутствии нагрузок и включении линии на напряжение, равное разности напряжений по концам линии D E = U А – U Б.
|
|
|
Уравнительный ток, протекающий под действием D E, будет вычисляться по формуле
. (2.57)
Уравнительная мощность, протекающая возле пункта А, равна
. (2.58)
Потокораспределение в схеме будет определяться по выражениям:
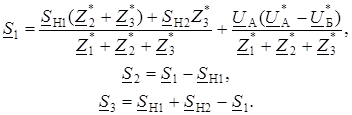(2.59)
|
|
|
