 |
Технические системы передачи информации
|
|
|
|
Первым техническим средством передачи информации на расстояние стал телеграф, изобретенный в 1837 году американцем Сэмюэлем Морзе. В 1876 году американец А.Белл изобретает телефон. На основании открытия немецким физиком Генрихом Герцем электромагнитных волн (1886 г.), А.С. Поповым в России в 1895 году и почти одновременно с ним в 1896 году Г.Маркони в Италии, было изобретено радио. Телевидение и Интернет появились в ХХ веке.
Все перечисленные технические способы информационной связи основаны на передаче на расстояние физического (электрического или электромагнитного) сигнала и подчиняются некоторым общим законам. Исследованием этих законов занимается теория связи, возникшая в 1920-х годах. Математический аппарат теории связи — математическую теорию связи, разработал американский ученый Клод Шеннон.

Клод Элвуд Шеннон (1916–2001), США
Клодом Шенноном была предложена модель процесса передачи информации по техническим каналам связи, представленная схемой.

Техническая система передачи информации
Под кодированием здесь понимается любое преобразование информации, идущей от источника, в форму, пригодную для ее передачи по каналу связи. Декодирование — обратное преобразование сигнальной последовательности.
Работу такой схемы можно пояснить на знакомом всем процессе разговора по телефону. Источником информации является говорящий человек. Кодирующим устройством — микрофон телефонной трубки, с помощью которого звуковые волны (речь) преобразуются в электрические сигналы. Каналом связи является телефонная сеть (провода, коммутаторы телефонных узлов, через которые проходит сигнал). Декодирующим устройством является телефонная трубка (наушник) слушающего человека — приемника информации. Здесь пришедший электрический сигнал превращается в звук.
|
|
|
Современные компьютерные системы передачи информации — компьютерные сети, работают по тому же принципу. Есть процесс кодирования, преобразующий двоичный компьютерный код в физический сигнал того типа, который передается по каналу связи. Декодирование заключается в обратном преобразовании передаваемого сигнала в компьютерный код. Например, при использовании телефонных линий в компьютерных сетях функции кодирования-декодирования выполняет прибор, который называется модемом.
Пропускная способность канала и скорость передачи информации
Разработчикам технических систем передачи информации приходится решать две взаимосвязанные задачи: как обеспечить наибольшую скорость передачи информации и как уменьшить потери информации при передаче. Клод Шеннон был первым ученым, взявшимся за решение этих задач и создавшим новую для того времени науку — теорию информации.
К.Шеннон определил способ измерения количества информации, передаваемой по каналам связи. Им было введено понятие пропускной способности канала, как максимально возможной скорости передачи информации. Эта скорость измеряется в битах в секунду (а также килобитах в секунду, мегабитах в секунду).
Пропускная способность канала связи зависит от его технической реализации. Например, в компьютерных сетях используются следующие средства связи:
— телефонные линии,
— электрическая кабельная связь,
— оптоволоконная кабельная связь,
— радиосвязь.
Пропускная способность телефонных линий — десятки, сотни Кбит/с; пропускная способность оптоволоконных линий и линий радиосвязи измеряется десятками и сотнями Мбит/с.
Шум, защита от шума
Термином “шум” называют разного рода помехи, искажающие передаваемый сигнал и приводящие к потере информации. Такие помехи прежде всего возникают по техническим причинам: плохое качество линий связи, незащищенность друг от друга различных потоков информации, передаваемых по одним и тем же каналам. Иногда, беседуя по телефону, мы слышим шум, треск, мешающие понять собеседника, или на наш разговор накладывается разговор совсем других людей.
|
|
|
Наличие шума приводит к потере передаваемой информации. В таких случаях необходима защита от шума.
В первую очередь применяются технические способы защиты каналов связи от воздействия шумов. Например, использование экранированного кабеля вместо “голого” провода; применение разного рода фильтров, отделяющих полезный сигнал от шума, и пр.
Клодом Шенноном была разработана теория кодирования, дающая методы борьбы с шумом. Одна из важных идей этой теории состоит в том, что передаваемый по линии связи код должен быть избыточным. За счет этого потеря какой-то части информации при передаче может быть компенсирована. Например, если при разговоре по телефону вас плохо слышно, то, повторяя каждое слово дважды, вы имеете больше шансов на то, что собеседник поймет вас правильно.
Однако нельзя делать избыточность слишком большой. Это приведет к задержкам и удорожанию связи. Теория кодирования позволяет получить такой код, который будет оптимальным. При этом избыточность передаваемой информации будет минимально возможной, а достоверность принятой информации — максимальной.
В современных системах цифровой связи для борьбы с потерей информации при передаче часто применяется следующий прием. Все сообщение разбивается на порции — пакеты. Для каждого пакета вычисляется контрольная сумма (сумма двоичных цифр), которая передается вместе с данным пакетом. В месте приема заново вычисляется контрольная сумма принятого пакета и, если она не совпадает с первоначальной суммой, передача данного пакета повторяется. Так будет происходить до тех пор, пока исходная и конечная контрольные суммы не совпадут.
Методические рекомендации
Рассматривая передачу информации в пропедевтическом и базовом курсах информатики, прежде всего следует обсудить эту тему с позиции человека как получателя информации. Способность к получению информации из окружающего мира — важнейшее условие существования человека. Органы чувств человека — это информационные каналы человеческого организма, осуществляющее связь человека с внешней средой. По этому признаку информацию делят на зрительную, звуковую, обонятельную, тактильную, вкусовую. Обоснование того факта, что вкус, обоняние и осязание несут человеку информацию, заключается в следующем: мы помним запахи знакомых объектов, вкус знакомой пищи, на ощупь узнаем знакомые предметы. А содержимое нашей памяти — это сохраненная информация.
|
|
|
Следует рассказать ученикам, что в мире животных информационная роль органов чувств отличается от человеческой. Важную информационную функцию для животных выполняет обоняние. Обостренное обоняние служебных собак используется правоохранительными органами для поиска преступников, обнаружения наркотиков и пр. Зрительное и звуковое восприятие животных отличается от человеческого. Например, известно, что летучие мыши слышат ультразвук, а кошки видят в темноте (с точки зрения человека).
В рамках данной темы ученики должны уметь приводить конкретные примеры процесса передачи информации, определять для этих примеров источник, приемник информации, используемые каналы передачи информации.
При изучении информатики в старших классах следует познакомить учеников с основными положениями технической теории связи: понятия кодирование, декодирование, скорость передачи информации, пропускная способность канала, шум, защита от шума. Эти вопросы могут быть рассмотрены в рамках темы “Технические средства компьютерных сетей”.
Представление чисел
Числа в математике
Число—важнейшее понятие математики, которое складывалось и развивалось в течение длительного периода истории человечества. Люди начали работать с числами еще с первобытных времен. Первоначально человек оперировал лишь целыми положительными числами, которые называются натуральными числами: 1, 2, 3, 4, … Долго существовало мнение о том, что есть самое большое число, “боле сего несть человеческому уму разумевати” (так писали в старославянских математических трактатах).
|
|
|
Развитие математической науки привело к выводу, что самого большого числа нет. С математической точки зрения ряд натуральных чисел бесконечен, т.е. неограничен. С появлением в математике понятия отрицательного числа (Р.Декарт, XVII век в Европе; в Индии значительно раньше) оказалось, что множество целых чисел неограниченно как “слева”, так и “справа”. Математическое множество целых чисел дискретно и неограниченно (бесконечно).
Понятие вещественного (или действительного) числа в математику ввел Исаак Ньютон в XVIII веке. С математической точки зрения множество вещественных чисел бесконечно и непрерывно. Оно включает в себя множество целых чисел и еще бесконечное множество нецелых чисел. Между двумя любыми точками на числовой оси лежит бесконечное множество вещественных чисел. С понятием вещественного числа связано представление о непрерывной числовой оси, любой точке которой соответствует вещественное число.
Далее будет говориться об особенностях представления чисел в вычислительных устройствах: компьютерах, калькуляторах.
Представление целых чисел
В памяти компьютера числа хранятся в двоичной системе счисления (см. “ Системы счисления ” 2). Есть две формы представления целых чисел в компьютере: целые без знака и целые со знаком.
Целые без знака — это множество положительных чисел в диапазоне [0, 2 k –1], где k — это разрядность ячейки памяти, выделяемой под число. Например, если под целое число выделяется ячейка памяти размером в 16 разрядов (2 байта), то самое большое число будет таким:
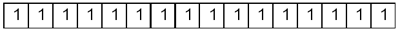
В десятичной системе счисления это соответствует: 216 – 1 = 65 535
Если во всех разрядах ячейки нули, то это будет ноль. Таким образом, в 16-разрядной ячейке помещается 216 = 65 536 целых чисел.
Целые числа со знаком — это множество положительных и отрицательных чисел в диапазоне [–2 k –1, 2 k –1 – 1]. Например, при k = 16 диапазон представления целых чисел: [–32 768, 32 767]. Старший разряд ячейки памяти хранит знак числа: 0 — число положительное, 1 — число отрицательное. Самое большое положительное число 32 767 имеет следующее представление:

Например, десятичное число 255 после перевода в двоичную систему счисления и вписывания в 16-разрядную ячейку памяти будет иметь следующее внутреннее представление:

Отрицательные целые числа представляются в дополнительном коде. Дополнительный код положительного числа N — это такое его двоичное представление, которое при сложении с кодом числа N дает значение 2 k. Здесь k — количество разрядов в ячейке памяти. Например, дополнительный код числа 255 будет следующим:
|
|
|

Это и есть представление отрицательного числа –255. Сложим коды чисел 255 и –255:

Единичка в старшем разряде “выпала” из ячейки, поэтому сумма получилась равной нулю. Но так и должно быть: N + (– N) = 0. Процессор компьютера операцию вычитания выполняет как сложение с дополнительным кодом вычитаемого числа. При этом переполнение ячейки (выход за предельные значения) не вызывает прерывания выполнения программы. Это обстоятельство программист обязан знать и учитывать!
Формат представления вещественных чисел в компьютере называется форматом с плавающей точкой. Вещественное число R представляется в виде произведения мантиссы m на основание системы счисления n в некоторой целой степени p, которую называют порядком: R = m? np.
Представление числа в форме с плавающей точкой неоднозначно. Например, для десятичного числа 25,324 справедливы следующие равенства:
25,324 = 2,5324? 101 = 0,0025324? 104 = 2532,4? 10–2 и т.п.
Чтобы не было неоднозначности, договорились в ЭВМ использовать нормализованное представление числа в форме с плавающей точкой. Мантисса в нормализованном представлении должна удовлетворять условию: 0,1 n  m < 1 n. Иначе говоря, мантисса меньше единицы и первая значащая цифра — не ноль. В некоторых случаях условие нормализации принимают следующим: 1 n
m < 1 n. Иначе говоря, мантисса меньше единицы и первая значащая цифра — не ноль. В некоторых случаях условие нормализации принимают следующим: 1 n  m < 10 n.
m < 10 n.
В памяти компьютера мантисса представляется как целое число, содержащее только значащие цифры (0 целых и запятая не хранятся). Следовательно, внутреннее представление вещественного числа сводится к представлению пары целых чисел: мантиссы и порядка.
В разных типах компьютеров применяются различные варианты представления чисел в форме с плавающей точкой. Рассмотрим один из вариантов внутреннего представления вещественного числа в четырехбайтовой ячейке памяти.
В ячейке должна содержаться следующая информация о числе: знак числа, порядок и значащие цифры мантиссы.

В старшем бите 1-го байта хранится знак числа: 0 обозначает плюс, 1 — минус. Оставшиеся 7 бит первого байта содержат машинный порядок. В следующих трех байтах хранятся значащие цифры мантиссы (24 разряда).
В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до 1111111. Значит, машинный порядок изменяется в диапазоне от 0 до 127 (в десятичной системе счисления). Всего 128 значений. Порядок, очевидно, может быть как положительным, так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка: от –64 до 63.
Машинный порядок смещен относительно математического и имеет только положительные значения. Смещение выбирается так, чтобы минимальному математическому значению порядка соответствовал ноль.
Связь между машинным порядком (Mp) и математическим (p) в рассматриваемом случае выражается формулой: Mp = p + 64.
Полученная формула записана в десятичной системе. В двоичной системе формула имеет вид: Mp2 = p2 + 100 00002.
Для записи внутреннего представления вещественного числа необходимо:
1) перевести модуль данного числа в двоичную систему счисления с 24 значащими цифрами,
2) нормализовать двоичное число,
3) найти машинный порядок в двоичной системе счисления,
4) учитывая знак числа, выписать его представление в четырехбайтовом машинном слове.
Пример. Записать внутреннее представление числа 250,1875 в форме с плавающей точкой.
Решение
1. Переведем его в двоичную систему счисления с 24 значащими цифрами:
250,187510 = 11111010,00110000000000002.
2. Запишем в форме нормализованного двоичного числа с плавающей точкой:
0,111110100011000000000000 Ч 1021000.
Здесь мантисса, основание системы счисления
(210 = 102) и порядок (810 = 10002) записаны в двоичной системе.
3. Вычислим машинный порядок в двоичной системе счисления:
Mp2 = 1000 + 100 0000 = 100 1000.
4. Запишем представление числа в четырехбайтовой ячейке памяти с учетом знака числа

Шестнадцатеричная форма: 48FA3000.
Диапазон вещественных чисел значительно шире диапазона целых чисел. Положительные и отрицательные числа расположены симметрично относительно нуля. Следовательно, максимальное и минимальное числа равны между собой по модулю.
Наименьшее по абсолютной величине число равно нулю. Наибольшее по абсолютной величине число в форме с плавающей точкой — это число с самой большой мантиссой и самым большим порядком.
Для четырехбайтового машинного слова таким числом будет:
0,111111111111111111111111 · 1021111111.
После перевода в десятичную систему счисления получим:
MAX = (1 – 2–24) · 263  1019.
1019.
Если при вычислениях с вещественными числами результат выходит за пределы допустимого диапазона, то выполнение программы прерывается. Такое происходит, например, при делении на ноль, или на очень маленькое число, близкое к нулю.
Вещественные числа, разрядность мантиссы которых превышает число разрядов, выделенных под мантиссу в ячейке памяти, представляются в компьютере приближенно (с “обрезанной” мантиссой). Например, рациональное десятичное число 0,1 в компьютере будет представлено приближенно (округленно), поскольку в двоичной системе счисления его мантисса имеет бесконечное число цифр. Следствием такой приближенности является погрешность машинных вычислений с вещественными числами.
Вычисления с вещественными числами компьютер выполняет приближенно. Погрешность таких вычислений называют погрешностью машинных округлений.
Множество вещественных чисел, точно представимых в памяти компьютера в форме с плавающей точкой, является ограниченным и дискретным. Дискретность является следствием ограниченного числа разрядов мантиссы, о чем говорилось выше.
Количество вещественных чисел, точно представимых в памяти компьютера, можно вычислить по формуле: N = 2 t · (U – L + 1) + 1. Здесь t — количество двоичных разрядов мантиссы; U — максимальное значение математического порядка; L — минимальное значение порядка. Для рассмотренного выше варианта представления (t = 24, U = 63,
L = –64) получается: N = 2 146 683 548.
Методические рекомендации
Тема представления числовой информации в компьютере присутствует как в стандарте для основной школы, так и для старших классов.
В основной школе (базовый курс) достаточно рассмотреть представление целых чисел в компьютере. Изучение этого вопроса возможно только после знакомства с темой “Системы счисления”. Кроме того, из принципов архитектуры ЭВМ ученики должны знать о том, что компьютер работает с двоичной системой счисления.
Рассматривая представление целых чисел, основное внимание нужно обращать на ограниченность диапазона целых чисел, на связь этого диапазона с разрядностью выделяемой ячейки памяти — k. Для положительных чисел (без знака): [0, 2 k –1], для положительных и отрицательных чисел (со знаком): [–2 k –1, 2 k –1 – 1].
Получение внутреннего представления чисел следует разбирать на примерах. После чего, по аналогии, ученики должны самостоятельно решать такие задачи.
Пример 1. Получить внутреннее представление в формате “со знаком” целого числа 1607 в двухбайтовой ячейке памяти.
Решение
1) Перевести число в двоичную систему счисления: 160710 = 110010001112.
2) Дописывая слева нули до 16 разрядов, получим внутреннее представление этого числа в ячейке:

Желательно показать, как для сжатой формы записи этого кода используется шестнадцатеричная форма, которая получается заменой каждой четверки двоичных цифр одной шестнадцатеричной цифрой: 0647 (см. “ Системы счисления ” 2).
Более сложной является задача получения внутреннего представления отрицательного целого числа (– N) — дополнительного кода. Нужно показать ученикам алгоритм этой процедуры:
1) получить внутреннее представление положительного числа N;
2) получить обратный код этого числа заменой 0 на 1 и 1 на 0;
3) к полученному числу прибавить 1.
Пример 2. Получить внутреннее представление целого отрицательного числа –1607 в двухбайтовой ячейке памяти.
Решение
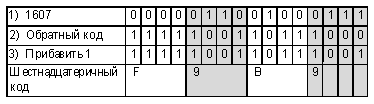
Полезно показать ученикам, как выглядит внутреннее представление самого маленького отрицательного числа. В двухбайтовой ячейке это –32 768.
1) легко перевести число 32 768 в двоичную систему счисления, поскольку 32 768 = 215. Следовательно, в двоичной системе это:
2) запишем обратный код:
3) прибавим единицу к этому двоичному числу, получим

Единичка в первом бите обозначает знак “минус”. Не нужно думать, что полученный код — это минус ноль. Это –32 768 в форме дополнительного кода. Таковы правила машинного представления целых чисел.
Показав этот пример, предложите ученикам самостоятельно доказать, что при сложении кодов чисел 32 767 + (–32 768) получится код числа –1.
Согласно стандарту, представление вещественных чисел должно изучаться в старших классах. При изучении информатики в 10–11-х классах на базовом уровне достаточно качественно рассказать ученикам об основных особенностях работы компьютера с вещественными числами: об ограниченности диапазона и прерывании работы программы при выходе за него; о погрешности машинных вычислений с вещественными числами, о том, что вычисления с вещественными числами компьютер производит медленнее, чем с целыми числами.
Изучение на профильном уровне требует подробного разбора способов представления вещественных чисел в формате с плавающей точкой, анализа особенностей выполнения вычислений на компьютере с вещественными числами. Очень важной проблемой здесь является оценка погрешности вычислений, предупреждение от потери значения, от прерывания работы программы. Подробный материал по этим вопросам имеется в учебном пособии [1].
Система счисления
Система счисления — это способ изображения чисел и соответствующие ему правила действия над числами. Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами.
В непозиционных системах счисления значение цифры не зависит от положения в числе.
Примером непозиционной системы счисления является римская система (римские цифры). В римской системе в качестве цифр используются латинские буквы:

Пример 1. Число CCXXXII складывается из двух сотен, трех десятков и двух единиц и равно двумстам тридцати двум.
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа — большая, то их значения вычитаются.
Пример 2.
VI = 5 + 1 = 6; IV = 5 – 1 = 4.
Пример 3.
MCMXCVIII = 1000 + (–100 + 1000) +
+ (–10 + 100) + 5 + 1 + 1 + 1 = 1998.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием позиционной системы счисления.
Система счисления, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, т.к. запись любых чисел производится с помощью десяти цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Позиционный характер этой системы легко понять на примере любого многозначного числа. Например, в числе 333 первая тройка означает три сотни, вторая — три десятка, третья — три единицы.
Для записи чисел в позиционной системе с основанием n нужно иметь алфавит из n цифр. Обычно для этого при n < 10 используют n первых арабских цифр, а при n > 10 к десяти арабским цифрам добавляют буквы. Вот примеры алфавитов нескольких систем:

Если требуется указать основание системы, к которой относится число, то оно приписывается нижним индексом к этому числу. Например:
1011012, 36718, 3B8F16.
В системе счисления с основанием q (q -ичная система счисления) единицами разрядов служат последовательные степени числа q. q единиц какого-либо разряда образуют единицу следующего разряда. Для записи числа в q -ичной системе счисления требуется q различных знаков (цифр), изображающих числа 0, 1,..., q – 1. Запись числа q в q -ичной системе счисления имеет вид 10.
|
|
|


