Развернутая форма записи числа

Пусть Aq — число в системе с основанием q, аi — цифры данной системы счисления, присутствующие в записи числа A, n + 1 — число разрядов целой части числа, m — число разрядов дробной части числа:

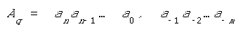
Развернутой формой числа А называется запись в виде:

Например, для десятичного числа:

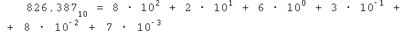
В следующих примерах приводится развернутая форма шестнадцатеричного и двоичного чисел:

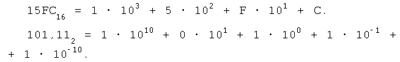
В любой системе счисления ее основание записывается как 10.

Если все слагаемые в развернутой форме недесятичного числа представить в десятичной системе и вычислить полученное выражение по правилам десятичной арифметики, то получится число в десятичной системе, равное данному. По этому принципу производится перевод из недесятичной системы в десятичную. Например, перевод в десятичную систему написанных выше чисел производится так:

Перевод десятичных чисел в другие системы счисления

Перевод целых чисел

Целое десятичное число X требуется перевести в систему с основанием q: X = (a _n a _n-1… a ₁ a ₀)_q.Нужно найти значащие цифры числа: .Представим число в развернутой форме и выполним тождественное преобразование:

Отсюда видно, что a 0есть остаток от деления числа X на число q. Выражение в скобках — целое частное от этого деления. Обозначим его за X 1. Выполняя аналогичные преобразования, получим:

Следовательно, a ₁ есть остаток от деления X 1 на q. Продолжая деление с остатком, будем получать последовательность цифр искомого числа. Цифра an в этой цепочке делений будет последним частным, меньшим q.

Сформулируем полученное правило: для того чтобы перевести целое десятичное число в систему счисления с другим основанием, нужно:

1) основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить по правилам десятичной арифметики;

2) последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя;

3) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;

4) составить число в новой системе счисления, записывая его, начиная с последнего частного.

Пример 1. Перевести число 37₁₀ в двоичную систему.

Для обозначения цифр в записи числа используем символику: a ₅ a ₄ a ₃ a ₂ a ₁ a ₀

Отсюда: 37₁₀ = l00l0l₂

Пример 2. Перевести десятичное число 315 в восьмеричную и в шестнадцатеричную системы:

Отсюда следует: 315₁₀ = 473₈ = 13B₁₆. Напомним, что 11₁₀ = B₁₆.

Десятичную дробь X < 1 требуется перевести в систему с основанием q: X = (0, a _–1 a _–2 … a _–m+1 a _–m)_q.Нужно найти значащие цифры числа: a _–1, a _–2, …, a _–m.Представим число в развернутой форме и умножим его на q:

Отсюда видно, что a –1есть целая часть произведения X на число q. Обозначим за X 1дробную часть произведения и умножим ее на q:

Следовательно, a _–2есть целая часть произведения X 1 на число q. Продолжая умножения, будем получать последовательность цифр. Теперь сформулируем правило: для того чтобы перевести десятичную дробь в систему счисления с другим основанием, нужно:

1) последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления;

2) полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;

3) составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.

Пример 3. Перевести десятичную дробь 0,1875 в двоичную, восьмеричную и шестнадцатеричную системы.

Здесь в левом столбце находится целая часть чисел, а в правом — дробная.

Отсюда: 0,1875₁₀ = 0,0011₂ = 0,14₈ = 0,3₁₆

Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой).

Методические рекомендации

Тема “Системы счисления” имеет прямое отношение к математической теории чисел. Однако в школьном курсе математики она, как правило, не изучается. Необходимость изучения этой темы в курсе информатики связана с тем фактом, что числа в памяти компьютера представлены в двоичной системе счисления, а для внешнего представления содержимого памяти, адресов памяти используют шестнадцатеричную или восьмеричную системы. Это одна из традиционных тем курса информатики или программирования. Являясь смежной с математикой, данная тема вносит вклад также и в фундаментальное математическое образование школьников.

Для курса информатики основной интерес представляет знакомство с двоичной системой счисления. Применение двоичной системы счисления в ЭВМ может рассматриваться в двух аспектах: 1) двоичная нумерация, 2) двоичная арифметика, т.е. выполнение арифметических вычислений над двоичными числами.

Двоичная нумерация

С двоичной нумерацией ученики встречаются в теме “Представление текста в компьютерной памяти”. Рассказывая о таблице кодировки, учитель должен сообщить ученикам, что внутренний двоичный код символа — это его порядковый номер в двоичной системе счисления. Например, номер буквы S в таблице ASCII равен 83. Восьмиразрядный двоичный код буквы S равен значению этого числа в двоичной системе счисления: 01010011.

Двоичные вычисления

Согласно принципу Джона фон Неймана, компьютер производит вычисления в двоичной системе счисления. В рамках базового курса достаточно ограничиться рассмотрением вычислений с целыми двоичными числами. Для выполнения вычислений с многозначными числами необходимо знать правила сложения и правила умножения однозначных чисел. Вот эти правила:

Принцип перестановочности сложения и умножения работает во всех системах счисления. Приемы выполнения вычислений с многозначными числами в двоичной системе аналогичны десятичной. Иначе говоря, процедуры сложения, вычитания и умножения “столбиком” и деления “уголком” в двоичной системе производятся так же, как и в десятичной.

Рассмотрим правила вычитания и деления двоичных чисел. Операция вычитания является обратной по отношению к сложению. Из приведенной выше таблицы сложения следуют правила вычитания:

0 — 0 = 0; 1 — 0 = 1; 10 — 1 = 1.

Вот пример вычитания многозначных чисел:

Полученный результат можно проверить сложением разности с вычитаемым. Должно получиться уменьшаемое число.

Деление — операция обратная умножению.
В любой системе счисления делить на 0 нельзя. Результат деления на 1 равен делимому. Деление двоичного числа на 10₂ ведет к перемещению запятой на один разряд влево, подобно десятичному делению на десять. Например:

Деление на 100 смещает запятую на 2 разряда влево и т.д. В базовом курсе можно не рассматривать сложные примеры деления многозначных двоичных чисел. Хотя способные ученики могут справиться и с ними, поняв общие принципы.

Представление информации, хранящейся в компьютерной памяти в ее истинном двоичном виде, весьма громоздко из-за большого количества цифр. Имеется в виду запись такой информации на бумаге или вывод ее на экран. Для этих целей принято использовать смешанные двоично-восьмеричную или двоично-шестнадцатеричную системы.

Существует простая связь между двоичным и шестнадцатеричным представлением числа. При переводе числа из одной системы в другую одной шестнадцатеричной цифре соответствует четырехразрядный двоичный код. Это соответствие отражено в двоично-шестнадцатеричной таблице:

Двоично-шестнадцатеричная таблица

Такая связь основана на том, что 16 = 2⁴ и число различных четырехразрядных комбинаций из цифр 0 и 1 равно 16: от 0000 до 1111. Поэтому перевод чисел из шестнадцатеричных в двоичные и обратно производится путем формальной перекодировки по двоично-шестнадцатеричной таблице.

Вот пример перевода 32-разрядного двоичного кода в 16-ричную систему:

1011 1100 0001 0110 1011 1111 0010 1010 BC16BF2A

Если дано шестнадцатеричное представление внутренней информации, то его легко перевести в двоичный код. Преимущество шестнадцатеричного представления состоит в том, что оно в 4 раза короче двоичного. Желательно, чтобы ученики запомнили двоично-шестнадцатеричную таблицу. Тогда действительно для них шестнадцатеричное представление станет эквивалентным двоичному.

В двоично-восьмеричной системе каждой восьмеричной цифре соответствует триада двоичных цифр. Эта система позволяет сократить двоичный код в 3 раза.

 

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: