Системы массового обслуживания в торговле

Входной поток заявок, очередь, узел обслуживания и выходной поток образует систему массового обслуживания (СМО). Состояния СМО ме­няются скачкообразно в случайные моменты времени. Входящий поток заявок для большинства СМО предполагается пуассоновским с интен­сивностью (средне число заявок в единицу времени). Длитель­ность обслуживания определяется числом заявок, обслуживаемых од­ним узлом в единицу времени с интенсивностью:

Динамика перехода состояний СМО описывается системой дифферен­циальных уравнений, решение которых позволяет определить вероятно­сти нахождения системы в одном из дискретных состояний, причем

Различают несколько видов СМО.

СМО с неограниченной длиной очереди: модель типа (М/М/п):

Для этого вида СМО отсутствие отказа в обслуживании, т.е.

следовательно, все заявки будут выполнены и

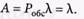Абсолютная про­пускная способность системы определяется соотношением

 

Остальные показатели СМО определяются по следующим моделям:

где интенсивность загрузки системы.

Эта вероятность определяет среднюю долю времени простоя каналов обслуживания, например, в течение рабочего дня. Вероятность занято­сти обслуживанием к заявок:

На этом основании вероятность или доля времени занятости обслу­живанием всех каналов системы:

Если же все каналы уже заняты обслуживанием, то вероятность со­стояния определяется так:

где величина (к-п) определяет длину очереди

Тогда вероятность оказаться в очереди равна вероятности застать все каналы уже занятыми обслуживанием:

Среднее число заявок, находящихся в очереди и ожидающих обслу­живания, составит:

Среднее время ожидания заявки в очереди:

 

Среднее время пребывания заявки в СМО:

Среднее число занятых в обслуживании каналов:

Вычисляем число свободных каналов:

Определяем коэффициент занятости каналов обслуживанием:

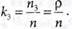
Находим среднее число заявок СМО:

Общие издержки — С, связанные с пребыванием в очереди одного покупателя в течение единицы времени, руб/час:

п — число каналов обслуживания;

λ — интенсивность входного потока, чел/час;

C_or — издержки, связанные с пребыванием в очереди одного покупа­теля в течение единицы времени, руб/час;

t_or — среднее время ожидания в очереди, час;

c_k — затраты на содержания, обслуживающей единицы

СМО с отказами: модель типа

Для определения основных показателей СМО с отказами пользуются следующими зависимостями:

Находим вероятность или время простоя каналов обслуживания, т.е. когда нет заявок:

Вычисляем вероятность отказа в обслуживании, т.е. все каналы об­служивания заняты, n = к:

так как в системах с отказами , то вероятность обслуживания можно определять по формуле:

Определяем относительную пропускную способность СМО:

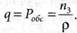
Вычисляем коэффициент занятости обслуживанием каналов:

Определяем вероятность занятости каналов обслуживанием:

Откуда можно определить среднее время простоя каналов:

Находим абсолютную пропускную способность СМО:

Следует отметить, что процесс обслуживания будет стабильным при Если в системе окажется, что , то СМО будет работать неус­тойчиво.

СМО с ожиданием с ограниченной длиной очереди: модель типа

Отказы в обслуживании наступают в том случае, когда число заявок k превышает сумму числа каналов обслуживания и максимально воз­можную длину очереди т.

Определяем вероятность простоя каналов обслуживания системы при отсутствии заявок:

Вычисляем вероятность обслуживания или относительную пропу­скную способность системы:

Вероятность отказа в обслуживании, когда все п каналов и т заявок заняты:

Определяем абсолютную пропускную способность:

Вычисляем среднее число занятых обслуживанием каналов:

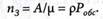
Находим среднее число заявок в очереди:

 

Определяем среднее число заявок в системе:

Находим вероятность наличия очереди в системе:

Вычисляем вероятность того, что все каналы заняты обслуживанием и поступившей заявке придется стать в очередь:

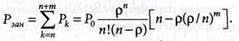
Определим среднее время ожидания обслуживания:

Находим среднее время пребывания заявки в системе:

Пример 11.1

Определить оптимальное число телефонных номеров в магазине при условии, что заявки на переговоры поступает с интенсивностью λ = 80 зая­вок в час, а средняя продолжительность разговора по телефону составляет

t_o6c = 1,5 мин.

Решение

СМО типа

1. Определяем интенсивность потока обслуживания:

2. Определяем интенсивность нагрузки:

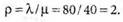
3. Находим вероятность простоя каналов (для п = 1):

4. Для заявок, получивших отказ в переговорах составляет:

5. Определяем вероятность обслуживания поступающих заявок:

6. Находим среднее число занятых обслуживанием каналов:

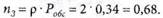
7. Вычисляем коэффициент занятости канала обслуживания:

8. Определяем пропускную способность системы:

9. Вычислим основные параметры системы аналогично, пологая п = 2, 3, 4, 5, 6. Результаты вычислений сведем в таблицу 11.1:

Таблица 11.1

Из таблицы 11.1 видно, что оптимальное число телефонных номеров п = 5, так как в этом случае доля обслуженных заявок составляет 96 % и только 4 % получает отказ, а абсолютная пропускная способность состав­ляет 77 заявок в час.

Пример 11.2

Городской универсам получает овощи с интенсивностью 6 машин в день. В магазине работают 3 фасовщика, каждый из которых в среднем может обработать товар с одной машины в течение t_o6 = 4 часов. Продол­жительность рабочего дня составляет T = 12 часов. Определить емкость подсобных помещений, чтобы вероятность полной обработки товаров была

Решение

СМО типа

1. Определяем интенсивность потока обслуживания:

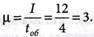
2. Вычисляем интенсивность загрузки фасовщиков:

3. Определяем вероятность обслуживания для различных значений m (полагая т = 2, 3,..., n) и сравниваем с допускаемой вероятностью полной обработки товаров. Вероятность простоя фасовщиков для т = 2.

4. Вычисляем вероятность отказа в обслуживании:

5. Находим вероятность обслуживания:

6. Определяем характеристики СМО для т = 3, так как условие огра­ничения не выполняется:

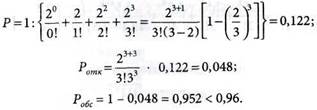
7. Определяем соответствующие характеристики СМО, полагая т = 4:

P_обс = 1- 0,031 = 0,969 > 0,96

Ответ: т = 4.

Пример 11.3

На оптовую базу прибывают автомашины с промышленными това­рами. Поток простейший поступает с интенсивностью λ = 1 авто/час. На территории базы могут одновременно находится не более 3-х машин, ожидающих разгрузки. Имеющиеся на базе 4 бригады грузчиков разгру­жают прибывающие машины. Среднее время разгрузки 1-й машины со­ставляет t = 2,5 ч. Необходимо определить основные показатели СМО оптовой базы, если рабочий день составляет 8 часов.

Решение

СМО типа

1. Определяем интенсивность потока обслуживания:

2. Определяем интенсивность загрузки системы:

3. Определяем вероятность простоя машин:

4. Определим вероятность отказа:

5. Определяем вероятность обслуживания:

6. Определяем пропускную способность системы:

7. Вероятность застать все машины, занятых обслуживанием:

8. Вероятность оказаться в очереди, поступающих заявок:

9. Определим длину очереди:

10. Определим среднее время ожидания в очереди:

 

11. Определяем среднее время разгрузки машин:

12. Найдем коэффициент занятости бригады:

13. Среднее число машин на базе:

14. Среднее число занятых обслуживанием бригад:

Пример 11.4

В магазин самообслуживания поступает пуассоновский поток поку­пателей с интенсивностью человек в минуту. Средняя продолжитель­ность обслуживания на расчетном узле составляет Уровень суммарных потерь связан с простоем среднего числа свободных контро­леров-кассиров 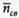и пребыванием среднего числа покупателей в очереди . 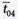Построить график зависимости суммы среднего числа свободных контролеров-кассиров и среднего числа покупателей в очереди от числа контролеров-кассиров п, Определить по нему оптимальное число контролеров-кассиров при котором суммарные по­тери будут минимальными. = 0,5 пок./мин.

Решение

Для данной задачи СМО типа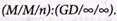

Найдем

где — интенсивность потока обслуживания покупателей;

— интенсивность поступления покупателей.

Интенсивность нагрузки системы = 0,5-1,8 = 0,9.

Для одного узла расчета, т.е. п = 1.

1. Вероятность простоя 1 узла расчета, когда нет заявок:

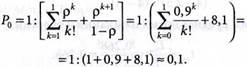
т.е. 10% времени узел расчета не занят.

2. Вероятность образования очереди:

3. Среднее число покупателей, находящихся в очереди:

4. Число узлов, не занятых обслуживанием:

5. Среднее число покупателей для одного узла расчета:

6. Коэффициент занятости узла расчета

Так как очередь к узлу расчета длинная: 8, то приведем аналогичные расчеты для 2-х узлов расчета. Суммарные потери

Для 2-х узлов расчета, т.е. п = 2

1. Вероятность простоя

т.е. 38 % времени узлы не заняты.

2. Вероятность образования очереди:

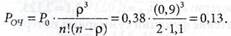
3. Среднее число покупателей, находящихся в очереди (длина оче­реди):

4. Число узлов не занятых обслуживанием:

5. Среднее число покупателей:

6. Коэффициент занятости для 2-х узлов расчета:

Суммарные потери:

Для 3-х узлов расчета, т.е. п = 3.

1. Вероятность простоя:

т.е. 40 % времени узлы не заняты.

2. Вероятность очереди:

3. Среднее число покупателей, находящихся в очереди:

4. Число узлов, не занятых обслуживанием:

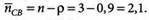
5. Среднее число покупателей:

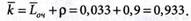
1. Коэффициент занятости для 2-х узлов расчета:

Суммарные потери: = 0,023 + 2,1 = 2,123.

Построим значение функции суммарных потерь:

 

Рис. 11.3

f (2) = 1,34,

f (3) = 2,123.

f_min = f (2) = 1,34.

Ответ: п = 2.

Контрольные вопросы

1. Чем определяется структурная модель элементарной системы массо­вого обслуживания (СМО) в торговле?

2. Сформулируйте постановку задач обслуживания в торговле.

3. Назовите основные параметры СМО с отказами.

4. Чем определяется СМО с неограниченным ожиданием?

5. Что представляет собой СМО смешанного типа?

6. Какой поток называется простейшим?

7. Что представляют собой Марковские цепи?

Задачи 11.1-11.16

Задача 11.1

В магазин самообслуживания поступает пуассоновский поток поку­пателей с интенсивностью 150 пок./час. Средняя продолжительность об­служивания 4,5 мин. Уровень сумм потерь связан с простоем свободных кассиров и пребыванием покупателей в очереди Построить гра­фик зависимости сумм свободных кассиров и числа покупателей в оче­реди от числа кассиров, т.е. . Определить оптимальное число кассиров ,

Задача 11.2

В магазин самообслуживания поступает пуассоновский поток = = 200 пок/час; в течение дня их обслуживает 3 кассира с интенсивностью обслуживания = 120 пок./час. Определить вероятность образования очереди в магазине и среднюю длину очереди в течение дня. Най­ти число кассиров в часы «пик» = 300 пок./час и часы «спада» = = 100 пок./час, обеспечивающих такую же длину очереди и вероятность ее образования.

Задача 11.3

На оптовую базу прибывают автомашины с товарами. Поток про­стейший и поступает с интенсивностью 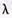= 4 авт./час. На территории

базы могут одновременно находиться не более 3 автомашин. Две брига­ды грузчиков разгружают машины в течение = 9,5 часов. Определить основные показатели СМО оптовой базы

Задаче 11.4

В магазин самообслуживания поступает пуассоновский поток поку­пателей с интенсивностью = 5 пок./мин. Средняя продолжительность обслуживания 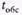= 3,0 мин. Уровень суммарных потерь связан с просто­ем свободных кассиров 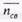и пребыванием покупателей в очереди Построить график зависимости суммарных свободных кассиров и числа покупателей в очереди от числа кассиров п, т.е. Определить оптимальное число кассиров

Задача 11.5

На оптовую базу прибывают автомашины с товарам. Поток простей­ший и поступает с интенсивностью = 2 авт./час. На территории базы могут одновременно находиться не более m = 3 автомашин, две бригады грузчиков разгружают машины в течение = 1,5 часов. Определить ос­новные показатели СМО оптовой базы Т = 6 часов.

Задача 11.6

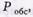Машины с товаром прибывают в универсам в неопределенное время в среднем 6 авт./день. Подсобные помещения и оборудование позволяют хранить товар объемом не более 3 автомашин одновременно. Четыре фа­совщика в среднем обрабатывают товар в течение дня. Определить вероятность обслуживания приходящей машины и емкость поме­щений чтобы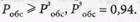

Задача 11.7

Машины с товаром прибывают в магазин в среднем 4 авт./день. Под­собные помещения и оборудование позволяют хранить товар объемом не более т = 2 автомашин одновременно. Три фасовщика в среднем об­рабатывают товар в течение 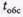= 0,5 дня. Определить вероятность об­служивания приходящей машины 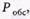и емкость помещений чтобы =5 0,98.

Задача 11.8

В магазин самообслуживания поступает пуассоновский поток поку­пателей с интенсивностью 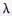= 3 пок/мин. Средняя продолжительность обслуживания = 1,5 мин. Уровень сумм потерь связан с простоем свободных кассиров и пребыванием покупателей в очереди Постро­ить график зависимости сумм кассиров и числа покупателей в очере­ди от числа кассиров п, т.е. Определить оптимальное число кассиров

Задача 11.9

В магазин самообслуживания поступает пуассоновский поток = = 120 пок./час; в течение дня их обслуживает 3 кассира. Средняя продол­жительность обслуживания составляет 2,5 мин. Определить вероятность образования очереди в магазине и среднюю длину очереди в тече­ние дня. Найти число кассиров в часы «пик» = 300 пок./час и часы «спада» 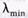= 100 пок./час, обеспечивающих такую же длину очереди и вероятность ее образования.

Задача 11.10

В магазин самообслуживания поступает пуассоновский поток = =8 200 пок./час; в течение дня их обслуживает 3 кассира с интенсивностью обслуживания 100 пок./час. Определить вероятность образования оче­реди в магазине и среднюю длину очереди в течение дня. Найти число кассиров в часы «пик» 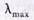= 320 пок./час и часы «спада» = = 80 пок./час, обеспечивающих такую же длину очереди 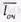и вероятность ее образования

Задача 11.11

Машины с товаром прибывают в универсам в неопределенное время в среднем 6 авт./день. Подсобные помещения и оборудование позволяют хранить товар объемом не более 3 автомашин одновременно. Четыре фа­совщика в среднем разгружают товар в течение 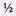дня. Определить веро­ятность обслуживания приходящей машины и емкость помещений

чтобы 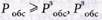= 0,94.

12	Поделиться:

Воспользуйтесь поиском по сайту: