Об идее a priori и о сомнении в опытном рассуждении

Человек по природе метафизик и горд; он мог поверить, что идеальные творения его духа, соответствующие его взглядам, представляют и самую действительность.

Метафизик, схоластик и экспериментатор действуют по идее

a priori. Различие состоит в том, что схоластик считает свою идею абсолютной истиной, которую он нашел и из которой выво­дит потом с помощью одной только логики все последствия Экспериментатор, более скромный, ставит, напротив, свою идею как вопрос, как предвзятое объяснение природы, более или менее вероятное, из которого логически выводит следствия, сличая их каждую минуту с действительностью посредством опыта. Та­ким образом, он идет от частных истин к истинам более общим, но никогда не дерзая думать, что нашел истину абсолютную.

Следовательно, экспериментальная идея тоже идея, но это идея, представляемая в виде гипотезы, следствия которой долж­ны быть подводимы под экспериментальный критерий, чтобы судить о ее справедливости.

Ум экспериментатора отличается от ума метафизика и схоластика скромностью, потому что каждую минуту опыт внушает ему сознание о его относительном и абсолютном невежестве. Научая человека, экспериментальная наука все более и более уменьшает его гордость, доказывает,ему каждый день, что пер­вые причины, также как и объективная реальность вещей, всег­да будут от него скрыты, и что он может познать только отно­шения. Такова на самом деле единственная цель всех наук.

Экспериментальная гипотеза должна быть всегда основана на предварительном наблюдении. Другое существенное условие гипотезы, чтобы она была так же вероятна, как и возможна, и чтобы она допускала проверку опытом. В самом деле, если бы

сделать гипотезу, которую нельзя поверить опытом, то этим самым мы вышли бы из экспериментального метода и впали бы в ошибки схоластиков и систематиков.

Нет определенных правил для того, чтобы по поводу данного наблюдения рождалась в мозгу правильная и плодотворная идея. Как скоро идея явилась, то можно только сказать, как нужно подчинять ее определенным правилам и точным логическим законам, от которых никакой экспериментатор не должен отступать; но ее появление совершенно самопроизвольно, и при­рода ее совершенно индивидуальна. Это особенное чувство, нечто составляющее оригинальность, изобретательность или гений каж­дого человека.

Итак, опытный метод не дает новых и плодотворных идей тому, у кого их нет; он послужит только к тому, чтобы у того, у кого есть идеи, дать им правильное направление и развить их для извлечения из них возможно лучших результатов. Идея — это зерно; метод — это почва, доставляющая ему условия для развития, процветания и принесения наилучших плодов сообраз­ных с его природой.

Люди, имеющие предчувствие новых истин, редки; во всех науках наибольшее число людей развивает н продолжает идеи небольшого числа других людей. Те, кто делает открытия, суть провозвестники новых и плодотворных идей. Обыкновенно имя открытия дают познанию нового факта, но, я думаю, что в действительности открытие составляет та идея, которая связана с открытым фактом. Факты сами по себе не бывают ни велики, ни малы. Великое открытие есть факт, который, появляясь в науке, породил светоносные идеи, сияние которых рассеяло темноту многих мест и показало новые пути.

Первое условие, которое должен выполнить ученый, предающийся исследованию естественных явлений, состоит в том, чтобы сохранять полную свободу ума, опирающуюся на философские сомнения. Не следует, однако же, быть скептиком: нужно верить в науку, т. е. в детерминизм, в абсолютные и необходимые отно­шения вещей, точно так же в явлениях, свойственных живым телам, как и во всяких других; но в то же время следует быть твердо уверенным, что мы знаем.эти отношения только более или менее приблизительным образом и что наши теории далеко не представляют неизменных истин.

Когда мы составляем в науках общую теорию, то мы вполне убеждены только в одной вещи — в том, что все эти теории, абсолютно говоря, ложны. Они составляют только частные и временные истины, которые необходимы нам как ступени, на кото­рых мы отдыхаем, чтобы потом идти дальше в исследовании; они представляют только настоящее состояние наших познаний и, следовательно, должны будут видоизменяться вместе с возра­станием науки и изменяться тем чаще, чем менее науки подви­нулись в своем развитии.

Если бы медик вообразил, что его рассуждения имеют вер­ность заключений математики, он впал бы в величайшую ошибку и пришел бы к самым ложным заключениям. К несчастью, это случалось и случается еще до сих пор с людьми, которых я назову систематиками. В самом деле, эти люди отправляются от идеи, более или менее основанной на опыте и принимаемой ими за абсолютную истину. Затем они логически рассуждают, не делая опытов от вывода к выводу, строят систему, вполне логиче­скую, но не имеющую никакой научной реальности. Поверхност­ные люди часто дают ослепить себя этой видимостью логики, и таким-то образом иногда и в наше время повторяются споры, достойные древней схоластики. Такая преувеличенная вера в рассуждение, ведущая физиолога к фальшивому упрощению ве­щей, с одной стороны, зависит от незнаний той науки, о которой он говорит, с другой стороны, от отсутствия чутья сложности естественных явлений. Вот отчего происходит, что иногда чистые математики, умы в других отношениях весьма большие, впадают в ошибки этого рода; они слишком упрощают и рассуждают о явлениях, как они себе их создали в уме, а не о тех, каковы они в природе.

Люди, питающие слишком большую веру в свои теории и в свои идеи, не только дурно настроены для того, чтобы делать открытия, но делают и очень плохие наблюдения. Они неизбежно наблюдают с предвзятой идеей; и когда учреждают опыт, то хотят видеть в его результатах только одно подтверждение своих теорий. Таким образом, они искажают наблюдение и часто пре­небрегают весьма важными фактами, потому что эти факты не ведут их к цели. Вот почему мы в другом месте сказали, что опыты следует делать никак не для подтверждения своих идей, а просто для их проверки; это значит, другими словами, что следует принимать результаты опыта так, как они нам представ­ляются со всеми их неожиданностями и случайностями.

Но, кроме того, весьма естественным образом бывает, что люди, слишком верящие в свои теории, недостаточно верят в теории других. Тогда господствующей мыслью этих порицателей чужих взглядов становится находить недостатки в чужих тео­риях и стараться всячески им противоречить. Неудобство для науки остается то же самое. Они делают опыты только для того, чтобы разрушить какую-нибудь теорию, вместо того чтобы делать их для отыскания истины. Они делают точно также дурные наблюдения, потому что из результатов своих опытов они берут только то, что годится для их цели, пренебрегая тем, что до нее не относится, и тщательно удаляя все то, что могло бы подтвердить идею, против которой они идут. Таким образом, эти два противоположных пути ведут к одному результату, т. е. к искажению науки и фактов.

Заключение из всего этого то, что перед решениями опыта следует откладывать как свое мнение, так и мнение других.

Когда идет спор и делаются опыты так, как мы сказали, т. е. с желанием во что бы то ни стало доказать предвзятую идею, то Ум уже не свободен и дело уже не в истине. Наука измельчается, и к ней примешиваются личная суетность и различные человеческие страсти. Между тем самолюбие не должно бы при­нимать никакого участия во всех этих напрасных спорах. Когда два физиолога или два медика воюют, каждый поддерживая свои идеи или свои теории, то посреди их противоречащих дока­зательств абсолютно верно только одно — то, что обе эти тео­рии недостаточны и что ни та, ни другая не представляют исти­ны. Итак, истинно научный дух должен бы делать нас скром­ными и благосклонными. Мы все, в сущности, знаем очень мало и все можем ошибиться при тех безмерных трудностях, какие нам представляет исследование естественных явлений. Самое лучшее, что мы можем сделать, будет — соединять наши усилия, а не разъединять их и не уничтожать взаимно личными спорами. Одним словом, ученый, который ищет истины, должен сохранять свой ум свободным, спокойным и, если бы это было возможно, никогда не допускать, как говорит Бэкон, чтобы его глаза были увлажаемы человеческими страстями.

Идеи и теории наших предшественников должны быть сохраняемы лишь настолько, насколько они представляют состояние науки, но им, очевидно, суждено измениться, если только мы не вздумаем утверждать, что наука не должна. делать прогресса, что невозможно.

 

В опытных науках дурно понятое уважение к личному авторитету было бы суеверием и составило бы действительное пре­пятствие успехам науки; в то же время, оно было бы противно примерам, представляемым нам великими людьми всех времен. В самом деле, великие люди суть именно те, которые принесли новые идеи и разрушили заблуждения. Итак, сами они не ува­жали авторитета своих предшественников и не признают того, чтобы и в отношении к ним действовали иначе.

Это неподчинение авторитету, освещаемое опытным, методом, как основное правило нисколько не противоречит уважению и удивлению, нами питаемому к великим людям, которые нам пред­шествовали и которым мы обязаны открытиями, составляющими основание нынешних наук.

Великих людей сравнивали с гигантами, на плечи которых взбираются пигмеи и видят дальше их самих. Это просто значит, что науки делают успехи после великих людей и именно вследствие их влияния. Откуда следует, что их преемники будут иметь более многочисленные научные познания, чем познания, которы­ми в свое время обладали великие люди. Но великий человек тем не менее остается великим человеком, т. е. гигантом.

Мы выше сказали, что экспериментатор, который видит подтверждение своей идеи опытом, должен ещё сомневаться и ис­кать поверки от противного.

 

В самом деле, чтобы с достоверностью заключить, что данное условие есть ближайшая причина явления, не достаточно иметь доказательства того, что всегда это условие предшествует явлению или сопровождает его; но надобно еще доказать, что явле­ние не будет иметь места, как скоро не будет существовать это условие. Если мы ограничимся одним только доказательством присутствия, то каждую минуту можно будет впасть в ошибку и предположить отношения причины к следствию тогда, когда на лицо только простое совпадение. Совпадения составляют, как мы это дальше увидим, одни из самых важных подводных кам­ней, какие встречают опытный метод в науках, сложных как био­логия.

Чтобы видеть, останется ли следствие, уничтожают предполагаемую причину, опираясь на старую и. абсолютно верную пого­ворку: Sublata causa, tollitur effecturs. Это означает также ехреrimentum crucis.

Есть медики, которые боятся и избегают поверки от против­ного; как только у них явились наблюдения, которые благоприят­ствуют их идеям, они не хотят искать противоречащих фактов из боязни увидеть свои гипотезы опровергнутыми. Мы сказали, что в этом виден весьма плохой ум: когда хотят найти истину, то твердо установить свои идеи можно только стараясь разру­шить свои собственные заключения противоопытами.

О философских препятствиях, встречаемых экспериментальной медициной

Система есть гипотеза, к которой логически сводятся факты с помощью рассуждения, но без критической экспериментальной поверки. Теория есть выверенная гипотеза, уже подлежавшая контролю рассуждения и экспериментальной критики. Если бы считали какую-нибудь теорию совершенной и если бы перестали проверять ее ежедневным научным опытом, то она сделалась бы доктриной. Следовательно доктрина есть теория, считаемая непоколебимой и принимаемая точкой отправления для дальней­ших выводов, которые считается уже ненужным подвергать экс­периментальной проверке.

Системы и доктрины индивидуальны; они имеют притязание быть неизменяемыми и сохранять свою личность. Экспериментальный метод, напротив, безличен, он уничтожает индивидуаль­ность тем, что соединяет и приносит в жертву частные идеи каж­дого и обращает их в пользу общей истины, устанавливаемой с помощью экспериментального критериума. Ход его медленный и трудный и в этом отношении он всегда будет менее нравиться уму. Системы, напротив, обольстительны, потому что они дают правильную абсолютную науку с помощью одной только логики; это увольняет от исследований и делает медицину легкой.

Итак, как экспериментатор, я избегаю философских систем, но я не могу из-за этого отказаться от того философского духа, который, не будучи нигде, есть повсюду и который, не принад­лежа ни к какой системе, должен парить не только над всеми науками, но и над всеми человеческими познаниями. Оттого-то, избегая философских систем, я сильно люблю философов и мне беспредельно приятно быть в их обществе.

В самом деле, с научной точки зрения философия представ­ляет вечное стремление человеческого разума к познанию неизвестного. Оттого философы всегда держатся в среде спорных вопросов и в возвышенных областях, на высших пределах наук. Этим они сообщают научной мысли движение, которое ее ожив­ляет и облагораживает, они укрепляют ум, развивая его общей интеллектуальной гимнастикой, и в то же время беспрестанно наводят его на необъятное решение великих задач; они поддер­живают таким образом некоторого рода жажду неизвестного и священный огонь исследования, который никогда не должен уга­сать в ученом. В самом деле, пламенное желание знания есть единственный двигатель, который возбуждает и поддерживает усилия исследователя; и именно это - то знание, которое он дейст­вительно схватывает и которое, однако, всегда убегает от него, составляет в одно и то же время и его единственную муку, и его единственное счастье. Кто не знает мук незнания, тот не поймет радостей открытия, которые поистине самые живые из радостей, которые когда-либо может чувствовать ум человека.

Но, по капризу нашей природы, эта радость открытия, кото­рой так ищут и так надеются, исчезает, как скоро найдена. Это только молния, озарившая нам другие горизонты, к которым ненасытное -наше любопытство стремится с еще большим жаром. От этого и в самой науке известное теряет свою привлекатель­ность, между тем как неизвестное всегда полно прелести.

Без этого постоянного возбуждения, сообщаемого жалом не­известного, без этой непрерывно возрождающейся научной жажды нужно было бы опасаться, чтобы ученый не завершил бы системы тем, что приобрел или узнал. Философия, непрестанно волнуя необъятную массу неразрешенных вопросов, возбуждает и поддерживает это здравое движение в науках. Ибо в том огра­ниченном смысле, в котором я рассматриваю здесь философию, ей принадлежит одно только неопределенное; определенное по необходимости переходит в область науки.

По-моему, настоящий философский ум тот, у которого возвышенные стремления оплодотворяют науки, увлекая их к исследованию истин, которые в настоящее время вне их, но которые не должны быть отрицаемы от того, что они удаляются и возвы­шаются все более и более, по мере того, как за них берутся фи­лософские умы более могучие и более тонкие. Будет ли конец этому стремлению человеческого ума? Найдет ли оно предел? Я не могу этого понять; но пока, как я и сказал выше, ученому ничего не остается делать лучше, как идти без остановки, пото­му что он всегда подвигается вперед.

Итак, одно из самых огромных препятствий, какие встречаются при этом общем и свободном ходе человеческих познаний, есть стремление, увлекающее различные познания к индивидуализированию в системы. Это вовсе не следствие, вытекающее из самых вещей, так как в природе все связано и нет ничего изоли­рованного и систематичного; но это результат стремления нашего ума, в одно и то же время слабого и властного. Наука, которая остановилась бы на системе, осталась бы в застое и изолирова­лась бы, ибо систематизация есть настоящая научная инцистация, а всякая инцистированная часть в организме перестает при­нимать участие в общей жизни этого организма.

Философия, непрестанно стремясь возвыситься, поднимает науку до высоты причины или источника вещей. Она ей показывает, что вне ее есть вопросы, мучащие человечество и еще не разрешенные им. Это прочное соединение науки и философии полезно обеим: оно возвышает одну и сдерживает другую.

Но как скоро связь, соединяющая философию с наукой, прерывается, философия, лишенная опоры или противовеса науки, уносится в неприступную высь и реет в облаках, между тем как наука, оставленная без направления и без возвышенного стрем­ления, падает, задерживается или идет наудачу.

Но если вместо того, чтобы держаться этого братского, союза, философия захотела бы вмешаться в хозяйство науки и догматически опекать ее в ее произведениях и в ее методах прояв­ления, тогда согласие не могло бы уже существовать.

Для того, чтобы делать научные наблюдения, опыты или открытия, методы и приемы философии слишком неопределенны и остаются немощными; для этого ничего нет кроме методов и приемов научных, часто очень специальных, которые могут быть известны только экспериментаторам, ученым или философам, занятым какой-нибудь определенной наукой.

Одним словом, если ученые полезны философам и философы, ученым, то ученый тем не менее остается свободным и хозяином у себя, а что касается до меня, я думаю, что ученые производят свои открытия, свои теории и свою науку без философов. Если бы встретились недоверяющие этому взгляду, то, может быть, легко было бы доказать им, как говорит Ж. де Мэстр, что те, которые сделали наиболее открытий в науке, менее всех знали Бэкона; между тем как те, которые читали его и размышляли над ним, подобно самому Бэкону, ничего не совершили. В самом деле, этим научным приемам и этим научным методам научаются только в лабораториях, когда экспериментатор борется с проблемами природы. Вот куда нужно прежде всего направить молодых людей; научная эрудиция и научная критика — удел молодого возраста; они могут принести плоды только когда наставле­ние в науке начато вес настоящем святилище, т.е. в лаборатории.

М. Вертгеймер ОТКРЫТИЕ ГАЛИЛЕЯ

 

 

Вертгеймер (Werthelmer) Макс (№ апреля 1880—12 октября 1943) — немецкий психолог, один из основателей гештальт-психологии, Профессор Берлинского (с 1922) университета, университета во Франкфурте-на-Майне (с 1929), по­сле эмиграции в США (1933) — профессор Школы социальных ис­следований в Нью-Йорке. Основа­тель и редактор (совместно с К. Коффкой и В. Келером) журна­ла «Psychologische Forschung» (1921), где публиковались работы гештальтпсихологов. В своей первой экспериментальной работе, посвященной исследованию видимого движения, М. Вертгеймер впервые выдвинул гипотезу о целостной структуре перцептивных процессов. Подход к изучению вос­принимаемого образа как целостной структуры (гештальта) явился ос­новным принципом гештальтпсихо-

логии, который затем был распространен и на другие психические процессы, в том. числе мышление. Согласно Вертгеймеру, мыслитель­ный процесс развивается как последовательная смена гештальтов — разных типов целостного видения проблемной ситуации, причем реше­ние задачи означает совпадение структуры видения этой ситуации с ее объективной структурой. В книге «Productive Thinking» (N. Y., 1945) Вертгеймер широко иллюстрирует основные принципы своего подхода, анализируя ряд известных научных открытий. В хрестоматии приводится одна из таких иллюстраций. Сочинения: Experimenteller studien uber das Schen von Bewegungen,— «Zeitschrift fur Psychologic», 1910—1911, Bd. 61, S. 3—4; Unter-suchungen zur lehre von. der ge-stalt— «Psychol. Forsch.», 1921, Bd. 1; 1923r Bd. 4.

 

Как Галилей совершил то открытие, которое привело к формулировке закона инерции и, таким образом, к возникновению со­временной физики?

Известен целый ряд попыток ответить на этот вопрос, одна­ко и до сих пор он остается не вполне ясным. Ситуация, в кото­рой находился Галилей, была отягощена крайне сложными понятиями и спекуляциями, касавшимися природы движения.

Предшествующие обсуждения центрировались на такого рода вопросах: Направлялось ли мышление Галилея индукцией или абстракцией? Опытным наблюдением и экспериментом или же некими априорными предложениями? Можно ли считать принципиальной заслугой Галилея то, что он превратил качественные наблюдения в количественные? и др.

Если изучить литературу — древние трактаты по физике и работы современников Галилея, — то можно обнаружить, что одной из самых замечательных черт мышления Галилея была его способность достигать предельно ясного структурного понимания (insight) на чрезвычайно сложном и запутанном фоне.

Я не буду пытаться дать здесь историческую реконструкцию. Это потребовало бы основательного анализа огромного материала первоисточников, а я не историк. К тому же доступный нам исторический материал все равно недостаточен для психолога, интересующегося деталями развивающегося процесса мысли, которые обычно опускаются в тексте. К сожалению, мы не можем расспросить самого Галилея о действительном ходе его мысли, хотя мне, например, и очень хотелось бы это сделать, особенно по поводу отдельных моментов. Моя попытка воссоздать некото­рые линии этого красивого процесса будет в известном смысле лишь психологической гипотезой, не претендующей на историче­скую правильность. Но, я думаю, что кое-что мы все-таки смо­жем извлечь из нее для решения нашей проблемы.

Я надеюсь, что читатель будет не только читать, но и попытается думать вместе со мной.

 

 

Ситуация следующая:

1) Если взять камень в руку и отпустить его, то он упадет вниз. Так происходит со всеми тяжелыми телами. Преж­ний физик сказал бы: «Тяжелые тела имеют тяготение к своему дому, земле».

2) Если толкнуть тело, скажем, повозку или мяч по горизонтальной плоскости, то оно придет в движение и будет дви­гаться некоторое время, пока не остановится. Остановка последует скорее, если толчок будет слабым, и, наоборот, несколько позже, если толчок будет сильным.

Это - самые простые значения старого термина. Рано или поздно движущееся тело остановится, если сила, толкав­шая его, перестанет действовать. Это очевидно.

3) Имеются некоторые дополнительные факторы, которые необходимо рассматривать в связи с анализом движения,

а именно: величина объекта, его форма, поверхность, по которой движется тело, наличие или отсутствие препятст­вий и т.д.

 

Итак, нам известно огромное число факторов, так или иначе касающихся движения. Все они хорошо нам знакомы. Но понимаем ли мы их? Кажется, что да. На самом деле, разве мы не знаем, чем вызывается движение?! Разве мы не можем усмотреть здесь действие некого принципа?

 

Галилея эти знания не удовлетворяли. Он спросил себя: «Знаем ли мы, как действительно происходит такое движение?» Побуждаемый желанием понять внутренние законы движения, Галилей сказал себе: «Мы знаем, что тяжелое тело падает, но как оно падает? При падении оно приобретает некоторую скорость. Скорость растет вместе с увеличением пройденного телом пути. Но как именно?»

Обыденный опыт дает нам лишь грубую картину происходя­щего. Галилей начал наблюдать и экспериментировать в надежде обнаружить, что же происходит со скоростью и подчиняется ли ее изменение каким-либо понятным принципам. Его эксперименты представляются чрезвычайно грубыми по сравнению с тем, что достигла фи­зика позже. Но, организуя эти наблюдения и эксперименты, Галилей пытался сформулиро­вать свою гипотезу.

Сначала он нашел формулу ускорения па­дающего тела. Так как скорость падения тела велика и было трудно установить ее точное зна­чение, то Галилей решил изучить этот вопрос, рассуждая так: «Не могу ли я исследовать дви­жение более надежным способом? Как я буду изучать, как шарик скатывается по наклонной плоскости. Разве свободное падение не есть лишь частный случай движения по наклонной плоскости, когда угол наклона достиг 90°?».

Изучая ускорение в различных случаях, он увидел, что оно уменьшается вместе с уменьшением» угла наклона (рис. 1). Величине угла соответствует величина уменьшения ускорения.

Ускорение стало самым главным и центральным фактом, как только Галилей усмотрел принципиальную связь уменьшения ускорения с уменьшением величины угла.

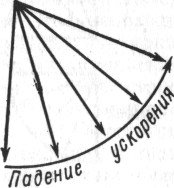
Рис. 1

Потом он вдруг спросил себя: «Не есть ли это лишь половина целой картины?» Не является ли то, что происходит, когда тело подбрасывают вверх или когда шар толкают в гору, другой симметричной частью той же самой картины, частью, которая как отражение в зеркале повторяет то, что есть у нас, и таким обра­зом сообщает картине полноту?

Когда тело подбрасывают вверх, мы имеем не положительное, а отрицательное ускорение. По мере подъема тела его скорость убывает. И опять, симметрично положительному ускорению падающего тела, это отрицательное ускорение уменьшается по мере того, как угол наклона все больше отклоняется от 90°, так что получается законченная, полная картина (рис. 2).

Рис. 2

Но полна ли и эта картина? Нет. В ней есть пробел. Что будет, когда плоскость горизонтальна, когда угол равен пулю, а тело находится в движении? Во всех случаях мы можем начинать с некоторой данной скорости. Что же тогда должно произой­ти в соответствии с нашей структурой?

Положительное ускорение вниз и отрицательное ускорение вверх уменьшаются при отклонении от вертикали до и не положительного, и не отрицательного ускорения, т.е. до постоянного движения?! Если тело движется го­ризонтально в данном направлении, оно будет продолжать двигаться с постоянной скоростью — вечно, если только некая внешняя сила не изменит состояния движения.

Это утверждение находится в крайнем противоречии с прежним положением, приведенным выше в п. 2. Тело, движущееся с постоян­ной скоростью, никогда не придет к состоянию покоя, если только не действуют внешние помехи, вне зависимости от того, была ли сила, приведшая тело в движение, сильной или слабой.

Что за странное заключение! Противоречащее на первый взгляд всему обыденному опыту и все-таки требуемое логикой структуры.

Конечно же, мы не можем выполнить такого эксперимента. Даже если бы мы могли устранить все внешние помехи, чего мы, разумеется, сделать не можем, возможность вечного наблюдения, конечно, исключена. С другой стороны, затухание измене­ния ускорения ясно указывает на нулевую величину этого изме­нения для данного случая.

Точка зрения Галилея подтвердилась и послужила основанием для развития современной физики.

Что существенно для этого описанного здесь процесса? Во-первых, желание выяснить, что же происходит, когда тело падает или скатывается вниз; желание посмотреть, нет ли во всех этих случаях некоего внутреннего принципа; желание рассмот­реть все случаи при различных углах наклона.

Это центрирует мысль на ускорении. Организация экспери­ментов определяется гипотезой о том, что центрация на вопросе об ускорении может привести к пояснению всей проблемы.

Различные случаи выступают как части некой хорошо упоря­доченной структуры, указывая на отношение, существующее между углами наклона и величиной ускорения. Каждый отдельный случай занимает свое место в группе, и то, что происходит в каж­дом из этих случаев, может быть понято как определяемое этим местом.

Вo-вторых, эта структура рассматривается теперь как часть более широкого контекста: существует и другая, дополнительная часть, понимаемая как симметричная к первой и формирующая целое, в котором эти две половинки представляют собой две больших, соответствующих друг другу подгруппы, с положитель­ным ускорением в одной, с отрицательным — в другой. Они ви­дятся теперь как бы с одной точки зрения, в согласованной структуре целого.

В-третьих, обнаруживается, что в этой структуре существует некая критическая точка — случай горизонтального движения. Структурный принцип целого задает ясную необходимость существования именно этой точки. С точки зрения этой необходи­мости случай горизонтального движения выступает как такой случай, при котором не происходит ни ускорения, ни замедления, как случай постоянной скорости. Следовательно, покой стано­вится только частным случаем движения с постоянной скоро­стью, случаем отсутствия положительного или отрицательного ускорения. Покой и постоянное прямолинейное движение в гори­зонтальном направлении выступают теперь как структурные экви­валенты.

Конечно, при этом используются и операции традиционной логики, такие, как индукция, вывод, формулировка теории, равно как и наблюдение, и изобретательное экспериментирование. Но все эти операции функционируют, занимая определенное место внутри целого процесса. Сам же этот процесс управляется той перецентрацией, которая проистекает из желания добиться ос­мысленного понимания. Это приводит к трансформации, в ре­зультате которой вещи видятся как части новой, ясной струк­туры.

Продуктивные процессы имеют зачастую следующую приро­ду: желание достичь подлинного понимания побуждает к иссле­дованию и запускает его. Определенная область в поле исследо­вания выделяется как критическая и центральная, но не стано­вится при этом изолированной. Складывается новая, более глу­бокая, структурная точка зрения на ситуацию, вызывая измене­ния в функциональных значениях отдельных элементов, в их группировке и т. д. Направляясь тем, чего требует структура ситуации для критической области, приходят к некоторому осмыс­ленному предсказанию, которое, точно так же, как и другие ча­сти этой структуры, требует верификации, прямой или косвенной.

Рассказывая эту историю, я часто с чувством глубокого удовлетворения видел, как у многих моих слушателей возникал жи­вой и искренний интерес. Следя за теми драматическими собы­тиями, которые происходили в головах у моих слушателей, я вдруг видел, как в самый критический момент некоторые из них восклицали: «Теперь я понимаю (See)!». Для них это был переход от знания некоторого разрозненного ряда вещей к углуб­ленному пониманию и осмысленному взгляду на целое.

А. Пуанкаре МАТЕМАТИЧЕСКОЕ ТВОРЧЕСТВО

 

Пуанкаре (Poincare) Жюль Анри (29 апреля 1854—17 июля 1912) — выдающийся французский матема­тик. Окончил Политехническую (1875) и Горную (1879) школы в Париже. Профессор Парижского университета (1886). Член Париж­ской Академии наук (1887). Работы А, Пуанкаре явились, с од­ной стороны, завершением класси­ческого направления в математике, и с другой — открыли путь ее совре­менным направлениям (таково, на­пример, создание качественной тео­рии дифференциальных уравнений). Пуанкаре — автор ряда открытий в математике, математической физике и других смежных областях.

 

 

Генезис математического творчества является проблемой, которая должна вызывать живейший интерес у психологов, Кажется, что в этом процессе человеческий ум меньше всего заимствует из внешнего мира и действует, или только кажется действующим, лишь сам по себе и сам над собой. Поэтому, изучая процесс математической мысли, мы можем надеяться постичь нечто са­мое существенное в человеческом сознании.

Это было понято уже давно, и несколько месяцев назад жур­нал «Математическое образование», издаваемый Лезаном и Фэром, опубликовал вопросник, касающийся умственных привычек и методов работы различных математиков. К тому моменту, когда были опубликованы результаты этого опроса, мой доклад был в основном уже подготовлен, так что я практически не мог ими воспользоваться. Отмечу лишь, что большинство ответов подтвердило мои заключения; я не говорю об единогласии, так как при всеобщем опросе на него и нельзя надеяться.

Первый факт, который должен нас удивлять, или, вернее, должен был бы удивлять, если бы к нему не привыкли, следующий: как получается, что существуют люди, не понимающие математики?

Тот факт, что не все способны на открытие, не содержит ничего таинственного. Можно понять и то, что не все могут запом­нить доказательство, которое когда-то узнали. Но то обстоятель­ство, что не всякий человек может понять математическое рассуждение, когда ему его излагают, кажется совершенно удивительным. И тем не менее людей, которые лишь с большим трудом воспринимают эти рассуждения, большинство; опыт учителя средней школы подтверждает это.

И далее, как возможна ошибка в математике? Нормальный разум не должен совершать логической ошибки, и тем не менее есть очень тонкие умы, которые не ошибутся в коротком рассуж­дении, подобном тем, с которыми ему приходится сталкиваться в обыденной жизни и которые не способны провести или повто­рить без ошибки более длинные математические доказательства, хотя в конечном счете последние являются совокупностью ма­леньких рассуждений, совершенно аналогичных тем, которые эти люди проводят так легко. Нужно ли прибавить, что и сами хо­рошие математики не являются непогрешимыми?

Ответ, как мне кажется, напрашивается сам собой. Предста­вим себе длинный ряд силлогизмов, у которых заключения пер­вых служат посылками следующих; мы способны уловить каж­дый из этих силлогизмов, и в переходах от посылки к рассужде­нию мы не рискуем ошибиться. Но иной раз проходит много времени между моментом, когда некоторое предложение мы встречаем в качестве заключения силлогизма, и моментом, когда мы вновь с ним встретимся в качестве посылки другого силло­гизма, когда много звеньев в цепи рассуждений, и может слу­читься, что предложение забыто или, что более серьезно, забыт его смысл. Таким образом, может случиться, что предложение заменяют другим, несколько от него отличным, или что его при­меняют в несколько ином смысле; и это приводит к ошибке.

Если математик должен воспользоваться некоторым прави­лом, естественно, он сначала его доказывает и в момент, когда это доказательство свежо в его памяти, он прекрасно понимает его смысл и пределы применения и поэтому не рискует его исказить. Но затем он применяет его механически, и если память его подведет, то правило может быть применено неверно. В качест­ве простого и почти вульгарного примера можно привести тот факт, что мы часто ошибаемся в вычислении, так как забыли таблицу умножения.

С этой точки зрения математические способности должны бы­ли бы сводиться к очень надежной памяти или к безупречному вниманию. Это качество подобно способности игрока в вист запоминать сброшенные карты или — на более высоком уров­не — способности шахматиста, который должен рассмотреть большое число комбинаций и все их держать в памяти. Каждый хороший математик должен был бы быть одновременно хорошим шахматистом и обратно; точно так же он должен бы быть хорошим вычислителем. Действительно, так иногда случается, и, например, Гаусс был одновременно гениальным геометром и рано проявившим себя очень хорошим вычислителем.

Но есть исключения, хотя, я, пожалуй, не прав, называя это исключениями, так как иначе исключения оказались бы более многочисленными, чем правила. Напротив, это Гаусс был исключением. Что касается меня, то я вынужден признать свою совер­шенную неспособность выполнить сложение без ошибки. Я был бы также очень плохим шахматистом, я мог бы хорошо рассчи­тать, что, совершив такой-то ход, я подвергся бы такой-то опас­ности; я рассмотрел бы много других ходов, которые я отбросил бы по другим причинам, и кончил бы тем, что совершил бы рассмотренный ход, забыв между делом об опасности, которую я раньше предвидел.

Одним словом, у меня неплохая память, но она недостаточна, чтобы сделать меня хорошим шахматистом. Почему же она меня не подводит в трудном математическом рассуждении? Это, очевидно, потому, что она руководствуется общей линией рассуж­дения. Математическое рассуждение не есть простая совокуп­ность силлогизмов: это силлогизмы, помешенные в определенном порядке, и порядок, в котором эти элементы расположены, го­раздо более важен, чем сами элементы. Если я чувствую этот порядок, так что вижу все рассуждение в целом, то мне не страш

⇐ Предыдущая78910111213141516

Поделиться:

Воспользуйтесь поиском по сайту: