Дифракция на дифракционной решетке

Одномерная дифракционная решетка представляет собой систему из большого числа одинаковых параллельных щелей, разделенных также одинаковыми непрозрачными промежутками. Если а и b – соответственно ширина прозрачного и непрозрачного промежутков, то величина d = а + b называется постоянной решетки или ее периодом , где N₀ – число щелей, приходящееся на единицу длины.

 

 

Дифракционные решетки изготовляют методом нанесения тонких штрихов (царапин) на поверхность стеклянной пластинки (прозрачная решетка) или металлического зеркала (отражательная решетка).

Дифракционной решеткой может служить совокупность большого числа любых неоднородностей (отверстий и преград) на плоскости или в объеме; в последнем случае решетка называется пространственной. Например, трехмерную пространственную решетку представляют собой кристаллы твердых тел.

Схема наблюдения дифракции на прозрачной решетке представлена на рис. 1.7.

Рис. 1.7. Дифракция на прозрачной решетке: 1 – дифракционная решетка; 2 – линза; 3 – экран

 

На дифракционную решетку падает пучок параллельных лучей перпендикулярно к плоскости, в которой лежат щели. Решетка 1 вызывает дифракцию световых лучей, и на экране 3, помещенном в фокальной плоскости линзы 2, образуется дифракционная картина. Явлению дифракции сопутствует явление интерференции – наложение когерентных дифрагированных волн друг на друга.

Каждая щель решетки дает дифракционную картину в соответствии c уже описанной. При этом дифракционные максимумы и минимумы налагаются друг на друга. Однако основные черты общей дифракционной картины определяются как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света.

Выберем пучки от каждой щели решетки, распространяющиеся под одинаковым углом φ к нормали к дифракционной решетке. Собранные линзой 3 в одну линию (проходящую через точку P экрана), эти лучи проинтерферируют. Если общее число щелей в решетке N, то и интерферируют между собой N пучков. Результат интерференции будет зависеть от разности хода Δ между пучками. Так как щели находятся друг от друга на одинаковых расстояниях, то и разности хода лучей, идущих от двух соседних щелей, будут для данного направления φ одинаковы в пределах всей решетки:

. (1.5)

Этой разности хода соответствует разность фаз

. (1.6)

Если

, (1.7)

то колебания от всех щелей придут в точку P в одинаковой фазе, и будут взаимно усиливать друг друга. Амплитуда колебаний в этой точке:

A_max = NA, (1.8)

где A – амплитуда колебания, посылаемого одной щелью под углом φ.

Из соотношений (1.5) и (1.6) получим условие максимумов интенсивности:

, k = 0, 1, 2... (1.9)

Максимумы, определяемые данным условием, называются главными. Число k дает порядок главного максимума. Центральный максимум представляет собой максимум нулевого порядка. По обе стороны от него располагаются максимумы 1-го, 2-го и т.д. порядков.

Интенсивность главных максимумов J_max в N² раз больше интенсивности J_φ, создаваемой в направлении φ одной щелью. Действительно, возведя равенство (1.7) в квадрат, получим:

J_max = N²J_j. (1.10)

Главные минимумы при дифракции света на дифракционной решетке наблюдаются под углами дифракции φ, соответствующими минимумам при дифракции на одной щели:

, k = 1, 2, 3... (1.11)

В этих направлениях каждая из щелей не дает света (сама себя гасит).

Более детальный анализ многолучевой интерференции в дифракционной решетке показывает, что в промежутках между соседними главными максимумами имеется (N – 1) дополнительных минимумов и соответственно (N – 2) вторичных максимумов, интенсивность которых пренебрежимо мала по сравнению с главными максимумами.

В монохроматическом свете дифракционная картина имеет вид узких и ярких главных максимумов, разделенных практически темными широкими промежутками. Таким образом, световая энергия, падающая на решетку, перераспределяется ею так, что большая ее часть приходится на максимумы, а в минимумы попадает незначительная часть энергии. При увеличении числа щелей яркость главных максимумов возрастает, а вторичных – уменьшается.

 

Рис. 1.8. Распределение освещенности при дифракции на дифракционной решетке

 

При освещении решетки белым светом условия максимума (1.9) и минимума (1.11) будут справедливы для всех длин волн, и дифракционный спектр будет в виде окрашенных максимумов для λ₁, λ₂, λ₃,... Как видно из формулы (1.9), в центре (φ = 0) будет белая полоса, максимум нулевого порядка для λ₁, λ₂, λ₃,.... По обе стороны от нулевого порядка будут располагаться максимумы 1, 2,... порядков для λ₁, λ₂,.... Эти максимумы, сливаясь друг с другом, образуют окрашенные полосы – спектры 1, 2,... порядков. Чем короче длина волны, тем ближе расположен максимум к центральному, что видно из выражения . При k = 1 возникнут два спектра первого порядка (правый и левый), расположенных фиолетовыми концами к центральной белой полосе
(λ_фиол < λ_красн); при k = 2, 3,... – спектры второго, третьего и т.д. порядков (рис. 1.9).

Рис. 1.9. Схематичная картина спектров

 

Установка, на которой выполняются задания данной лабораторной работы, схематически представлена на рис. 1.10.

 

Рис. 1.10.Внешний вид лабораторной установки:

1 – оптическая скамья, 2 – рейтеры, 3 – лазер с источником питания,
4 – дифракционная решетка, 5 – экран

Экран можно поворачивать под разными углами к падающему на него световому пучку. Этот прием, так называемая косая проекция, очень удобен для значительного растягивания дифракционных картин в поперечном направлении, что дает возможность без микроскопа и лупы рассматривать на экране различные подробности дифракционных явлений. Дифракцию можно наблюдать и на экране, расположенном на стене.

ВНИМАНИЕ! НАДО ПОМНИТЬ, ЧТО ПОПАДАНИЕ В ГЛАЗА ПРЯМОГО ЛАЗЕРНОГО ИЗЛУЧЕНИЯ ОПАСНО ДЛЯ ЗРЕНИЯ, ПОЭТОМУ ПРИ РАБОТЕ С ЛАЗЕРОМ НЕОБХОДИМО СОБЛЮДАТЬ ПРЕДОСТОРОЖНОСТИ. ВСЕ ВКЛЮЧЕНИЯ И ВЫКЛЮЧЕНИЯ УСТАНОВКИ ПРОИЗВОДЯТСЯ ТОЛЬКО ПРЕПОДАВАТЕЛЕМ ИЛИ ДЕЖУРНЫМ ЛАБОРАНТОМ. ВСЯКОЕ ПЕРЕМЕЩЕНИЕ ЛАЗЕРА КАК ВО ВКЛЮЧЕННОМ, ТАК И В ВЫКЛЮЧЕННОМ СОСТОЯНИИ СТУДЕНТАМ КАТЕГОРИЧЕСКИ ВОСПРЕЩАЕТСЯ.

 

Задание I. Измерение длины волны излучения газового лазера
с помощью дифракционной решетки

Направленность и пространственная когерентность излучения лазера позволяют применять лазерный световой пучок в ряде измерений без предварительной его коллимации. Эта особенность лазерного излучения используется, в частности, в опытах с дифракционной решеткой.

Измерения, выполняемые в данном задании, имеют целью определение длины волны излучения лазера λ. Для этого используется условие максимума при дифракции на дифракционной решетке (1.9), из которого:

, (1.12)

где d – постоянная решетки; k – порядок максимума; φ – угол, на который отклоняются лучи с длиной волны λ от своего первоначального распространения (рис. 1.11). Поскольку угол φ мал, то 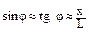. Расчетная формула будет иметь вид:

, (1.13)

где – среднее расстояние от центрального максимума () до максимума k порядка (среднее арифметическое отсчета справа и слева от центрального максимума).

Порядок выполнения задания

1. Подготовить установку к измерениям согласно рис. 1.10. Прямоугольный экран расположить нормально к оси лазера на расстоянии L от плоскости дифракционной решетки.

2. При включенном лазере установить дифракционную решетку перпендикулярно к оси светового луча, выходящего из лазера. Для этого путем вращения столика, несущего решетку, привести световой блик, отраженный назад к лазеру от плоскости решетки точно на середину выходного окна лазера, т.е. добиться совпадения выходящего из лазера светового пучка с его отражением от плоскости решетки.

3. Произвести измерения расстояния х слева и справа от максимума нулевого порядка до максимума k-го порядка. Результаты измерений занести в табл. 1.1.

4. Произвести измерения, аналогичные пункту 3 данного задания с другим расстоянием L между экраном и дифракционной решёткой.

 

Таблица 1.1

d, мм	L, мм	k	х слева, мм	х справа, мм	хср, мм	l,	lср,

 

5. Рассчитать длину волны излучения газового лазера, используя выражение (1.13), учитывая, что 1 мм = 10⁷ ( – ангстрем).

 

Задание II. Определение постоянной дифракционной решетки

Порядок выполнения задания

1. Подготовить установку к измерениям. На столик 3 поместить подставку с дифракционной решеткой. Прямоугольный экран расположить нормально к оси лазера на расстоянии L от дифракционной решетки. Необходимо проследить, чтобы плоскость дифракционной решетки была перпендикулярна лазерному лучу. После того как все детали установки помещены на соответствующие места, дежурный лаборант или преподаватель включает лазер.

2. Измерить расстояние х от центрального максимума до минимумов 1 и 2 порядка справа и слева от центрального максимума. Результаты занести в табл. 1.2.

3. Произвести измерения, аналогичные пункту 2 данного задания, с другим расстоянием L между экраном и дифракционной решеткой.

 

Таблица 1.2

l, мм	L, мм	k	х слева, мм	х справа, мм	xср, мм	d, мм	dср, мм

 

4. Рассчитать постоянную дифракционной решетки d из выражения (1.13), приняв длину волны излучения газового лазера l = 0,63 мкм.

Контрольные вопросы

1. Что такое явление дифракции. При каком условии оно наблюдается?

2. Какие волны называются когерентными?

3. Что такое интерференция волн, монохроматическое излучение?

4. Сформулируйте принцип Гюйгенса-Френеля.

5. В чем заключается метод зон Френеля?

6. Запишите условия минимума и максимума при дифракции на щели и поясните их.

7. Дифракция монохроматического света на дифракционной решетке. Условия главных максимумов.

8. Каковы основные особенности излучения лазера?

9. Как можно экспериментально определить длину волны лазерного излучения, постоянную дифракционной решетки?

ПОЛУЧЕНИЕ И ИССЛЕДОВАНИЕ

ПОЛЯРИЗОВАННОГО СВЕТА

 

Приборы и принадлежности – оптическая скамья, рейтеры, осветитель с регулируемым источником питания, поляроиды, черное зеркало с фоторезистором, стопы пластин с фоторезистором, фоторезистор, микроамперметр, экран.

Рис. 2.1.Внешний вид лабораторной установки: 1 – оптическая скамья, 2 – рейтеры, 3 – осветитель с регулируемым источником питания, 4 – поляроиды, 5 – черное зеркало с фоторезистором, 6 – стопы пластин с фоторезистором, 7 – микроамперметр, 8 – экран

Цель работы – изучение явления поляризации естественного света, проверка законов Малюса и Брюстера.

Теоретические сведения

С точки зрения электромагнитной теории свет представляет собой поперечную электромагнитную волну, в которой колебания векторов напряженности электрического и магнитного полей происходят перпендикулярно направлению распространения света (рис. 2.2).

Е и Н – вектора напряженности соответственно электрического и магнитного полей; С – вектор скорости распространения волны.

Вектор напряженности электрического поля волны Е часто называют световым вектором. Это обусловлено тем, что физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями электрического вектора.

Излучение светящегося тела слагается из волн, испускаемых отдельными атомами тела. Излучение отдельного атома продолжается 10^–8с. От каждого атома распространяются колебания Е и Н, происходящие в определенной плоскости (рис. 2.2). Мы же наблюдаем всегда суммарное действие многих атомов, а именно: множество всех возможных ориентировок Е и Н и быструю смену этих возможных ориентировок. Таким образом, свет, испускаемый обычными источниками, не имеет преимущественного направления колебаний, в нем представлены все направления колебаний Е, перпендикулярные к лучу. На рис. 2.3 показаны некоторые из возможных направлений колебаний вектора Е (вектор Н не указан).

Свет со всеми возможными ориентировками вектора Е (а следовательно, и вектора Н) называется естественным (рис. 2.3а). В естественном свете колебания различных направлений представлены с равной вероятностью (рис. 2.3).

Поляризованный свет – свет, в котором направления колебания вектора E каким-либо образом упорядочены.

Частично поляризованный свет (рис. 2.3б) – свет с преимущественным направлением колебаний вектора E.

Свет, в котором Е (а следовательно, и Н) имеет одно единственное направление, называется плоскополяризованным (рис. 2.3в).

Плоскость, проходящая через направление колебаний светового вектора Е и направление распространения волны, называется плоскостью поляризации.

На рис. 2.4 показано направление колебания вектора Е в плоскополяризованном свете. Из сказанного следует, что естественные источники света излучают волны не поляризованные.

Естественный свет можно преобразовать в плоскополяризованный, используя так называемые поляризаторы, пропускающие колебания только определенного направления.

Любой поляризатор может служить и анализатором, который предназначен для определения, поляризован свет или нет. В качестве поляризаторов и анализаторов используются пластина турмалина, поляроидные пленки, стопа Столетова, призма Николя и др.

Поставим на пути естественного света два поляроида, оси пропускания которых развернуты друг относительно друга на угол φ.

Вектор E_I световой волны после первого поляроида будет параллелен PP. Этот поляроид называют поляризатором, так как после него естественный свет стал поляризованным.

 

Рис. 2.5. Поляризация естественного света с помощью поляроида

 

После второго поляроида останется лишь вектор E_II, параллельный P'P' его плоскости пропускания: E_׀׀ = E₁cosj. Так как интенсивность света I ~ E², то после второго поляроида интенсивность будет

I = I₁×cos²j, (2.1)

где E₁ – интенсивность перед вторым поляроидом. Полученное соотношение между интенсивностями носит название закона Малюса. Если E₁ выразить через I₀, то закон Малюса примет вид

. (2.2)

Закон Малюса строго выполняется лишь для идеальных поляроидов – поляризатора и анализатора.

Если эти поляроиды частично пропускают свет с вектором E, перпендикулярным осям пропускания, то после поляризатора свет будет частично поляризован. Идеальный поляризатор при PP параллельном P'P' пропустит свет интенсивностью I_max, а при PP перпендикулярной P'P' – свет интенсивностью I_min.

Степенью поляризации частично-поляризованного света называется величина . При идеальном поляризаторе I_min = 0 и P = 1, свет плоскополяризован.

Если естественный свет падает на границу раздела двух диэлектриков, то отраженный и преломленный лучи являются частично поляризованными. В отраженном луче преобладают колебания, перпендикулярные плоскости падения, а в преломленном – колебания, лежащие в плоскости падения.

Рис. 2.6.Поляризация отраженного и преломленного лучей на границе раздела двух сред

 

Если угол падения равен углу Брюстера, который определяется соотношением

tg i_B = n₂₁, (2.3)

то отраженный луч является плоскополяризованным. Преломленный луч в этом случае поляризуется максимально, но не полностью. При этом отраженный и преломленный лучи взаимно перпендикулярны:

, .

Пусть угол падения i таков, что отраженный луч перпендикулярен преломленному, т.е. r = π/2 – i_B. Это условие называют условием Брюстера (рис. 2.6), а угол – углом Брюстера (i_B).

Рис. 2.7.Схематичное изображение законов отражения и преломления
на границе раздела двух сред

 

Используя закон преломления , получим формулу, определяющую угол Брюстера: .

При выполнении условия Брюстера тогда из формулы Френеля для получим:

.

Таким образом, при выполнении условия Брюстера, отраженный свет будет полностью поляризован в плоскости, перпендикулярной плоскости падения. Это утверждение носит название закона Брюстера.

Закон Брюстера имеет простое объяснение. Отраженная световая волна появляется за счет излучения электронов среды, совершающих вынужденные колебания под действием вектора преломленной волны. Это излучение имеет направленный характер: его интенсивность равна нулю в направлении колебаний зарядов. Направим под углом Брюстера на границу раздела плоскополяризованную волну с вектором , лежащим в плоскости падения.

Рис. 2.8.Диаграмма направленности излучения

 

На рис. 2.8 изображена диаграмма направленности излучения, возбужденного вектором . Нулевой минимум этой диаграммы при выполнении условия Брюстера совпадает по направлению с отраженным лучом.

Если вектор падающей волны направить перпендикулярно плоскости падения (рис. 2.9), то направление колебаний электронов будет перпендикулярно плоскости падения. Тогда диаграмма направленности будет развернута своим максимумом в направлении отраженного луча (рисунок ниже). Напомним, что пространственная форма диаграммы похожа на бублик без дырки.

Рис. 2.9.Диаграмма направленности излучения

Задание I. Проверка закона Малюса

1. Установить приборы на оптической скамье согласно рис. 2.10.

 

 

Рис. 2.10.Установка приборов на оптической скамье:

1 – осветитель, 2 – поляризатор, 3 – анализатор, 4 – фоторезистор

 

2. Подключить фоторезистор к микроамперметру.

3. Включить осветитель на максимальную мощность.

4. Установить угол между осями поляризации (пропускания) поляризатора и анализатора j = 0⁰. Для этого, вращая анализатор, добиться максимального значения фототока. При этом величины углов на угловой шкале поляризатора и анализатора должны быть одинаковыми.

5. Вращая анализатор, менять угол через каждые 10⁰ до 180⁰, записать соответствующие показания микроамперметра в табл. 2.1.

6. Построить график экспериментальной зависимости отношения от угла между осями пропускания j.

7. Построить график зависимости от .

8. Сделать выводы.

Таблица 2.1

j	I, мкА
…

 

Задание II. Проверка закона Брюстера

Поскольку отраженный от диэлектрической пластинки свет частично (или даже полностью) поляризован, проходящий свет также частично поляризуется и становится смешанным светом. Преимущественные колебания электрического вектора в прошедшем свете будут совершаться в плоскости падения. Максимальная, но не полная поляризация проходящего света достигается при падении под углом Брюстера. Для увеличения степени поляризации проходящего света используют стопу стеклянных пластинок, расположенных под углом Брюстера к падающему свету. В этом случае можно получить практически полностью поляризованный проходящий свет, так как каждое отражение ослабляет пропущенные колебания, перпендикулярные плоскости падения.

Упражнение 1. Проверка закона Брюстера с помощью черного зеркала.

1. Установить на оптической скамье приборы на уровне луча согласно рис. 2.11.

 

 

Рис. 2.11.Расположение приборов на оптической скамье:

1 – осветитель, 2 – поляризатор, 3 – анализатор, 4 – черное зеркало с фоторезистором

2. Подключить фоторезистор черного зеркала к микроамперметру.

3. Включить осветитель на максимальную мощность.

4. Установить углы на угловой шкале поляризатора и анализатора на 0^°.

5. Установить угловую шкалу на черном зеркале на отметке 90^°.

6. Вращая угловую шкалу на черном зеркале с изменением угла a через каждые 10^°, зафиксировать значения тока I₁ на микроамперметре.

7. Не меняя расположения приборов, установить 90^° на угловой шкале поляризатора и анализатора.

8. Вращая угловую шкалу на черном зеркале, изменяя угол a через каждые 10^°, зафиксировать значения тока I₂ на микроамперметре.

9. Результаты измерений занести в табл. 2.2.

10. Построить график зависимости фототока I₁ и I₂ от угла падения i на одном графике.

11. Определить угол Брюстера и рассчитать показатель преломления стекла черного зеркала.

12. Сделать соответствующие выводы.

Таблица 2.2

a	i = 90° – a	I1, мкА	I2, мкА
…

Дополнительное задание к упражнению 1

1. Установить на оптической скамье приборы согласно рис. 2.12.

 

Рис. 2.12.Приборы на оптической скамье:

1 – осветитель, 2 – поляризатор, 3 – черное зеркало с фоторезистором

 

2. Подключить фоторезистор черного зеркала к микроамперметру.

3. Включить осветитель на максимальную мощность.

4. Установить на угловой шкале поляризатора угол 180^°.

5. Установить угловую шкалу на черном зеркале под углом Брюстера.

6. Вращая угловую шкалу поляризатора, изменяя угол b через каждые 10^°, фиксируя значения фототока на микроамперметре.

7. Результаты измерений занести в табл.2.3.

8. Построить график зависимости от угла b.

9. Построить график зависимости от .

10. Сделать соответствующие выводы.

Таблица 2.3

b	I, мкА
…

 

Упражнение 2. Исследование поляризации света с помощью стеклянных пластин.

1. Установить на оптической скамье приборы согласно рис. 2.13.

 

Рис. 2.13. Расположение приборов на оптической скамье:

1 – осветитель, 2 – поляризатор, 3 – стопа пластин, 4 – фоторезистор

 

2. Подключить фоторезистор к микроамперметру.

3. Включить осветитель на максимальную мощность.

4. Установить на угловой шкале поляризатора угол 0^°.

5. Установить угловую шкалу на стопе стеклянных пластин под углом 90^°.

6. Вращая угловую шкалу стопы стеклянных пластин с изменением угла a через каждые 10^°, фиксировать значения фототока I₁ на микроамперметре.

7. Результаты измерений занести в табл. 2.4.

8. Установить на угловой шкале поляризатора угол 90^°.

9. Повторить пункт 6, фиксируя значения фототока I₂ на микроамперметре.

10. Результаты измерений занести в табл. 2.4.

11. Построить зависимости фототоков I₁, I₂, DI от угла падения луча i на стопу стеклянных пластин на одном графике.

12. По графику определить угол Брюстера и рассчитать показатель преломления для стекла стопы пластин.

13. Сделать соответствующие выводы.

Таблица 2.4

a	i = 90° – a	I1, мкА	I2, мкА	DI = (I2 – I1), мкА
…

 

Контрольные вопросы

1. Охарактеризуйте свет как электромагнитные волны. Что понимается под поперечностью световых волн.

2. Что такое интенсивность света?

3. В чем отличие естественного света, частично поляризованного света, плоскополяризованного света.

4. Какая плоскость называется плоскостью поляризации?

5. Что такое поляризатор? Что такое анализатор?

6. Сформулируйте закон Малюса.

7. Каковы способы поляризации естественного света?

8. Как формулируется Закон Брюстера?

9. Сделайте выводы по полученным результатам.

 

 

Список литературы

1. Савельев, И. В. Курс общей физики: учеб. пособие: в 3 т. Т. 3: Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц. / И. В. Савельев – Спб. и др.: Лань, 2008. – 317 с.

2. Курс физики: учеб. пособие для вузов по техн. специальностям и направлениям: в 2 т. / В.В. Арсентьев и др.; под ред. В.Н. Лозовского. –СПб. и др.: Лань. – т.1. – 2009. – 572 с.; т.2. – 2009. – 600 с.: ил.

3. Трофимова, Т. И. Курс физики: учеб. пособие для инж.-техн. специальностей вузов / Т. И. Трофимова. – М.: Academia, 2008. – 557 с.

4. Трофимова, Т. И. Краткий курс физики: учеб. пособие для вузов / Т. И. Трофимова. – М.: Высш. шк., 2009. – 531 с.

5. Детлаф, А.А. Курс физики: учеб. пособие для втузов / А. А. Детлаф, Б. М. Яворский. М.: Высш. шк., 2002. – 717 с.

6. Детлаф, А. А. Курс физики: учеб. пособие для вузов / А. А. Детлаф, Б. М. Яворский. – М.: Высш. шк., 2000. – 717 с.

7. Пронин, В. П. Практикум по физике для студентов сельскохозяйственных вузов / В. П. Пронин – СПб.: Лань, 2005. – 256 с.: ил.

8. Лабораторный практикум по физике: учеб. пособие для студентов втузов / А. С. Ахматов, В. М. Андреевский, А. И. Кулаков и др.; под ред. А. С. Ахматова. – М.: Высш. школа, 1980. – 360 с.

 

Оглавление

Введение………………………………………………………………..……3

ОБЩИН ПОЛОЖЕНИЯ О РАБОТЕ В ОПТИЧЕСКОЙ

ЛАБОРАТОРИИ……………………………………………………….……4

1. ИЗУЧЕНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ НА ДИФРАКЦИОННОЙ РЕШЕТКЕ……………………………………...6

2. ПОЛУЧЕНИЕ И ИССЛЕДОВАНИЕ ПОЛЯРИЗОВАННОГО

СВЕТА………………………………………………………………….......19

Список литературы………………………………………………………...30

 

 

Волновая оптика

Методические указания к выполнению лабораторных работ

для студентов всех специальностей

 

Составители ГОГЕЛАШВИЛИ Гоча Шотаевич

СТАВЕР Елена Юрьевна

ЦЕЛИЩЕВА Лариса Владимировна

 

Редактор П. Г. Павловская

 

 

Компьютерная набор и верстка Л. В. Целищева,

Е. Ю. Ставер

 

Подписано в печать Формат 60×84/16

Бумага офсетная. Печать офсетная.

Усл. печ. л.

Тираж __ 700 __экз. Заказ №. С-.

 

 

Марийский государственный технический университет

424000 Йошкар-Ола, пл. Ленина, 3

 

 

Редакционно-издательский центр

Марийского государственного технического университета

424006 Йошкар-Ола, ул. Панфилова, 17

 

12	Поделиться:

Воспользуйтесь поиском по сайту: