 |
Парная регрессия и корреляция в эконометрических системах
|
|
|
|
Теоритическая часть
«История развития эконометрики в России после 1987года»
Актуальность темы состоит в понимании того, что современная эконометрика есть быстроразвивающаяся отрасль науки, цель которой состоит в том, чтобы придать количественные меры экономическим отношениям. Иными словами, эконометрика изучает конкретные количественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей. Значение такого подхода в условиях современного микро- и макроэкономического развития переоценить не представляется возможным.
В связи со сказанным особый интерес представляет изучение основополагающих моментов истории институционализации эконометрики как научной статистико-математико-экономической дисциплины. В данном ключе важно выявить предпосылки возникновения эконометрической науки, специфику подходов различных экономических школ и экономистов, их роль и значение в процессе институционализации и современном развитии эконометрического знания.
В силу данных обстоятельств, изучение истории эконометрики в высшей степени актуально, отображает тенденции современного экономического развития, необходимо для понимания сущности эконометрической системы знаний.
Эконометрика - наука, изучающая количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей. Современное определение предмета эконометрики было выработано в уставе Эконометрического общества, которое главными целями назвало использование статистики и математики для развития экономической теории. Теоретическая эконометрика рассматривает статистические свойства оценок и испытаний, в то время как прикладная эконометрика занимается применением эконометрических методов для оценки экономических теорий. Эконометрика даёт инструментарий для экономических измерений, а также методологию оценки параметров моделей микро- и макроэкономики. Кроме того, эконометрика активно используется для прогнозирования экономических процессов как в масштабах экономики в целом, так и на уровне отдельных предприятий. При этом эконометрика является частью экономической теории, наряду с макро- и микроэкономикой.
|
|
|
Термин «эконометрика» состоит из двух частей: «эконо» - от «экономика» и «метрика» - от «измерение». Эконометрика входит в обширное семейство дисциплин, посвящённых измерениям и применению статистических методов в различных областях науки и практики. К этому семейству относятся, в частности, биометрия, технометрика, наукометрия, психометрия, хемометрия, квалиметрия. Особняком стоит социометрия - этот термин закрепился за статистическими методами анализа взаимоотношений в малых группах, то есть за небольшой частью такой дисциплины, как статистический анализ в социологии.
О развитии эконометрических методов
Современное состояние в эконометрике, как и в других областях, определяется прошлым. Кратко рассмотрим историю эконометрики и прикладной статистики, начав с их практической пользы.
Что дает прикладная статистика народному хозяйству? Так называлась статья, в которой приводились многочисленные примеры успешного использования методов эконометрики и прикладной математической статистики при решении практических задач. Обширный перечень примеров приведен в предыдущих главах настоящей книги. Его можно продолжать практически безгранично. Так, в любом номере журнала "Заводская лаборатория" есть работы, в которых те или иные методы эконометрики и прикладной статистики применяются для решения прикладных технико-экономических задач.
|
|
|
Поэтому бесспорно совершенно, что методы эконометрики и прикладной статистики успешно применяются в различных отраслях народного хозяйства, практически во всех областях науки. Согласно докладу, в 1988 г. затраты в СССР на статистический анализ данных оценивались в 2 миллиарда рублей ежегодно[1].
Большая практическая значимость эконометрики и прикладной статистики, особенно в экономике, менеджменте, технических исследованиях и разработках, оправдывает целесообразность развития их методологии, в которых эти области научной и прикладной деятельности рассматривалась бы как целое, "с высоты птичьего полета". Чтобы иметь возможность обсуждения тенденций развития эконометрики и статистических методов в XXI веке, необходимо хотя бы кратко рассмотреть их историю.
Об истории эконометрики и прикладной статистики. Типовые примеры раннего этапа применения статистических методов описаны в Ветхом Завете (см., например, Книгу Чисел). С математической точки зрения они сводились к подсчетам числа попаданий значений наблюдаемых признаков в определенные градации. В дальнейшем результаты стали представлять в виде таблиц и диаграмм, как это и сейчас делают Госкомстат РФ (Российское статистическое агентство). Надо признать, что по сравнению с Ветхим Заветом есть прогресс - в Библии не было таблиц. Однако нет продвижения по сравнению с работами российских статистиков конца девятнадцатого - начала двадцатого века (типовой монографией тех времен можно считать книгу, которая в настоящее время ещё легко доступна).
Сразу после возникновения теории вероятностей (Паскаль, Ферма, 17 век) вероятностные модели стали использоваться при обработке статистических данных. Например, изучалась частота рождения мальчиков и девочек, было установлено отличие вероятности рождения мальчика от 0.5, анализировались причины того, что в парижских приютах эта вероятность не та, что в самом Париже, и т.д. Имеется достаточно много публикаций по истории теории вероятностей, однако в некоторых из них имеются неточные утверждения, что заставило одного из крупнейших ученых ХХ в. академика Украинской АН Б.В. Гнеденко включить в очередное издание своего курса главу по истории математики случайного.
|
|
|
В 1794 г. (по другим данным - в 1795 г.) К. Гаусс разработал метод наименьших квадратов, один из наиболее популярных ныне статистических методов (см. главу 5 выше), и применил его при расчете орбиты астероида Церера - для борьбы с ошибками астрономических наблюдений. В Х1Х веке заметный вклад в развитие практической статистики внес бельгиец А. Кетле, на основе анализа большого числа реальных данных показавший устойчивость относительных статистических показателей, таких, как доля самоубийств среди всех смертей. Интересно, что основные идеи статистического приемочного контроля и сертификации продукции обсуждались академиком М.В. Остроградским и применялись в российской армии ещё в середине Х1Х в.. Статистические методы управления качеством, сертификации и классификации продукции и сейчас весьма актуальны.
Современный этап развития прикладной статистики можно отсчитывать с 1900 г., когда англичанин К. Пирсон основан журнал "Biometrika". Первая треть ХХ в. прошла под знаком параметрической статистики. Изучались методы, основанные на анализе данных из параметрических семейств распределений, описываемых кривыми из т.н. семейства Пирсона. Наиболее популярным было нормальное (гауссово) распределение. Для проверки гипотез использовались критерии Пирсона, Стьюдента, Фишера. Были предложены метод максимального правдоподобия, дисперсионный анализ, сформулированы основные идеи планирования эксперимента.
Разработанную в первой трети ХХ в. теорию называем параметрической статистикой, поскольку ее основной объект изучения - это выборки из распределений, описываемых одним или небольшим числом параметров. Наиболее общим является семейство кривых Пирсона, задаваемых четырьмя параметрами. Как правило, нельзя указать каких-либо веских причин, по которым конкретное распределение результатов наблюдений должно входить в то или иное параметрическое семейство. Исключения хорошо известны: если вероятностная модель предусматривает суммирование независимых случайных величин, то сумму естественно описывать нормальным распределением; если же в модели рассматривается произведение таких величин, то итог, видимо, приближается логарифмически нормальным распределением, и т.д. Однако в подавляющем большинстве реальных ситуаций подобных моделей нет, и приближение реального распределения с помощью кривых из семейства Пирсона или его подсемейств - чисто формальная операция.
|
|
|
Именно из таких соображений критиковал параметрическую статистику академик АН СССР С.Н. Бернштейн в 1927 г. в своем докладе на Всероссийском съезде математиков. Однако эта теория, к сожалению, до сих пор остается основой преподавания статистических методов и продолжает использоваться основной массой прикладников, остающихся далекими от новых веяний в статистике. Почему так происходит? Чтобы попытаться ответить на этот вопрос, обратимся к одной из статистических наук - наукометрии, в которой статистическими методами анализируется развитие научных исследований.
Точки роста
Отечественная литература по эконометрике и прикладной статистике столь же необозрима, как и мировая. Только в секции "Математические методы исследования" журнала "Заводская лаборатория" с 1960-х годов опубликовано более 1000 статей. Не будем даже пытаться перечислять коллективы исследователей или основные монографии в этой области. Отметим только одно издание. По нашему мнению, наилучшей отечественной книгой по прикладной статистике является сборник статистических таблиц Л.Н. Большева и Н.В.Смирнова с подробными комментариями, играющими роль сжатого учебника и справочника.
Основная цель настоящей главы - выделить и обсудить "точки роста" эконометрики и прикладной статистики, те их направления, которые представляются перспективными в будущем, в XXI веке, но пока в большинстве учебных изданий отодвинуты на задний план традиционными постановками.
При описании современного этапа развития эконометрических и статистических методов целесообразно выделить пять актуальных направлений, в которых развивается современная прикладная статистика, т.е. пять "точек роста": непараметрика (т.е. непараметрическая статистика), робастность, бутстреп, статистика интервальных данных, статистика нечисловых данных (в несколько иной терминологии - статистика объектов нечисловой природы).
Одна из ведущих научных школ в области статистики интервальных данных - это школа проф. А.П. Вощинина, активно работающая с конца 70-х годов. В частности, изучены проблемы регрессионного анализа, планирования эксперимента, сравнения альтернатив и принятия решений в условиях интервальной неопределенности.
|
|
|
Статистика объектов нечисловой природы как часть прикладной статистики. Согласно общепринятой в настоящее время классификации статистических методов прикладная статистика делится на следующие четыре области:
- статистика (числовых) случайных величин,
- многомерный статистический анализ,
- статистика временных рядов и случайных процессов,
- статистика объектов нечисловой природы.
Первые три из этих областей являются классическими. Они были хорошо известны еще в первой половине ХХ в. Остановимся на четвертой, сравнительно недавно вошедшей в массовое сознание специалистов. Ее именуют также статистикой нечисловых данных или попросту нечисловой статистикой. Анализ динамики развития эконометрики и прикладной статистики приводит к выводу, что в XXI в. она станет центральной областью прикладной статистики, поскольку содержит наиболее общие подходы и результаты[2].
В течение 70-х годов на основе запросов теории экспертных оценок (а также социологии, экономики, техники и медицины) развивались конкретные направления статистики объектов нечисловой природы. Были установлены связи между конкретными видами таких объектов, разработаны для них вероятностные модели. Научные итоги этого периода подведены в монографиях.
Следующий этап - выделение статистики объектов нечисловой природы в качестве самостоятельного направления в эконометрике и прикладной статистике, ядром которого являются методы статистического анализа данных произвольной природы. Программа развития этого нового научного направления впервые была сформулирована в статье. Реализация этой программы была осуществлена в 80-е годы. Для работ этого периода характерна сосредоточенность на внутренних проблемах нечисловой статистики. Ссылки на конкретные монографии, сборники, статьи и иные публикации нескольких десятков авторов приведены в главе 8. Отметим лишь сборник научных статей, полностью посвященный нечисловой статистике.
К 90-м годам статистика объектов нечисловой природы с теоретической точки зрения была достаточно хорошо развита, основные идеи, подходы и методы были разработаны и изучены математически, в частности, доказано достаточно много теорем. Однако она оставалась недостаточно апробированной на практике. Это было связано как с ее сравнительной молодостью, так и с общеизвестными особенностями организации науки в 80-е годы, когда отсутствовали достаточные стимулы к тому, чтобы теоретики занялись широким внедрением своих результатов. И в 90-е годы наступило время от математико-статистических исследований перейти к применению полученных результатов на практике.
Следует отметить, что в статистике объектов нечисловой природы, как и в других областях эконометрики, прикладной математической статистики и прикладной математики вообще, одна и та же математическая схема может с успехом применяться и в технических исследованиях, и в менеджменте, и в экономике, и в геологии, и в медицине, и в социологии, и для анализа экспертных оценок, и во многих иных областях, а потому ее лучше всего формулировать и изучать в наиболее общем виде, для объектов произвольной природы.
Сегодня эконометрика занимает достойное место в ряду экономических наук. В мире выпускается ряд научных журналов, полностью посвящённых эконометрике, в том числе: Journal of Econometrics (Швеция), Econometric Reviews (США), Econometrica (США), Sankhya. Indian Journal of Statistics. Ser.D. Quantitative Economics (Индия), Publications Econometriques (Франция)[. Эконометрику изучают в ведущих мировых университетах, пришло понимание, что без эконометрических методов невозможно проводить современный макро- и микроэкономический анализ.
На русском и казахском языке также существуют специализированные журналы. К ним относятся «Прикладная эконометрика» и «Квантиль». Отдельные публикации по эконометрике появляются в журналах «Экономика и математические методы», «Вопросы статистики», «Вопросы экономики» и некоторых других.
Ранее в по ряду причин эконометрика не была сформирована как самостоятельное направление научной и практической деятельности. Хотя в настоящее время начинают развертываться эконометрические исследования. В связи с этим начинается широкое преподавание этой дисциплины.
Контрольная работа №1
Парная регрессия и корреляция в эконометрических системах
По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн.руб) от объема капиталовложений (Х, млн. руб).
Требуется:
1. Для характеристики Y от Х построить следующие модели:
· Линейную;
· Степенную;
· Показательную;
· Гиперболическую.
2. Оценить каждую модель, определив:
· индекс корреляции;
· среднюю относительную ошибку;
· коэффициент детерминации;
· F – критерий Фишера.
1. Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.
2. Рассчитать прогнозные значения результативного признака, если прогнозное значение фактора увеличится на 110 % относительно среднего уровня.
3. результаты расчетов отобразить на графике.
Исходные данные:
| Вариант | Наблюдения | |||||||
Используем MS Еxcel для анализа полученных данных.
Вводим исходные данные для 1 варианта:

Для характеристики зависимости Y от Х построим следующие модели:
1) Линейная модель: у = а + bх,
где а, b – определяются методом наименьших квадратов (Гаусса)
b – коэффициент регрессии показывает, на сколько изменяется Y при изменении Х на единицу.

При анализе данных с помощью MS Еxcel получаем следующую зависимость:
у = 14,928144+ 0,432989*x
Индекс корреляции составил: r = 0,609207
Коэффициент детерминации составил: R2 = 0,371134
Средняя относительная ошибка E = 3,753212
F – критерий Фишера Fрасч = 2,9508
Fтабл = 6,61
Вывод: по критерию средняя относительная ошибка модель является значимой, т.к. E<20%, связь заметная r = 0,6092077 (r=0,5..0,7). По критерию Фишера модель нельзя назвать значимой, т.к. Fрасч < Fтабл. Также по коэффициенту детерминации R2 модель нельзя назвать значимой (<0,5).Из вышеизложенного можно сделать вывод, что в целом модель можно считать значимой, но результат моделирования должен быть подвергнут более тщательному анализу.
Степенная модель
Уравнение степенной модели имеет вид:  =a * xb
=a * xb
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:

Обозначим Y = lgy, X = lgx, A= lga.
Тогда уравнение примет вид: Y= А + b X – линейное уравнение регрессии.
где А и b определяются методом наименьших квадратов с помощью ЕХСЕL.

Исходное уравнение:

Далее получим:
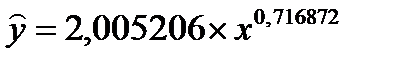
Индекс корреляции составил: r = 0,614873
Коэффициент детерминации составил: R2 = 0,378069
F – критерий Фишера Fрасч = 3,0395
Fтабл = 6,61
Вывод: по критерию средняя относительная ошибка модель является значимой, т.к. E<20%, связь заметная (r=0,5..0,7). По критерию Фишера модель нельзя назвать значимой, т.к. Fрасч < Fтабл. Также по коэффициенту детерминации R2 модель нельзя назвать значимой (<0,5). Из вышеизложенного можно сделать вывод, что в целом модель можно считать значимой, но результат моделирования должен быть подвергнут более тщательному анализу.
Показательная модель
Уравнение показательной кривой:
 .
.
После логарифмирования имеем:
 .
.
Обозначим Y = lgy, В = lgb, A= lga.
Тогда уравнение примет вид: Y= А + B x – линейное уравнение регрессии.
где А и В определяются методом наименьших квадратов с помощью MS Еxcel.

Уравнение имеет вид:

Далее получим:

Индекс корреляции составил: r = 0,619518
Коэффициент детерминации составил: R2 = 0,383803
F – критерий Фишера Fрасч = 3,114283
Fтабл = 6,61
Вывод: по критерию средняя относительная ошибка модель является значимой, т.к. E<20%, связь заметная (r=0,5..0,7). По критерию Фишера модель нельзя назвать значимой, т.к. Fрасч < Fтабл. Также по коэффициенту детерминации R2 модель нельзя назвать значимой (<0,5). Из вышеизложенного можно сделать вывод, что в целом модель можно считать значимой, но результат моделирования должен быть подвергнут более тщательному анализу.
Гиперболическая модель
Уравнение гиперболической функции:
 .
.
Произведем линеаризацию модели путем замены Х = 1/х.
В результате получим линейное уравнение у = а + bХ. Для перехода к исходным параметрам необходимо произвести обратную замену Х = 1/х.
где а и b определяются методом наименьших квадратов с помощью ЕХСЕL.

Имеет вид уравнение:

Индекс корреляции составил: r = 0,597011
Коэффициент детерминации составил: R2 = 0,356422
F – критерий Фишера Fрасч = 2,769068
Fтабл = 6,61
Вывод: по критерию средняя относительная ошибка модель является значимой, т.к. E<20%, связь заметная (r=0,5..0,7). По критерию Фишера модель нельзя назвать значимой, т.к. Fрасч < Fтабл. Также по коэффициенту детерминации R2 модель нельзя назвать значимой (<0,5). Из вышеизложенного можно сделать вывод, что в целом модель можно считать значимой, но результат моделирования должен быть подвергнут более тщательному анализу.
Сводная таблица EXCEL:

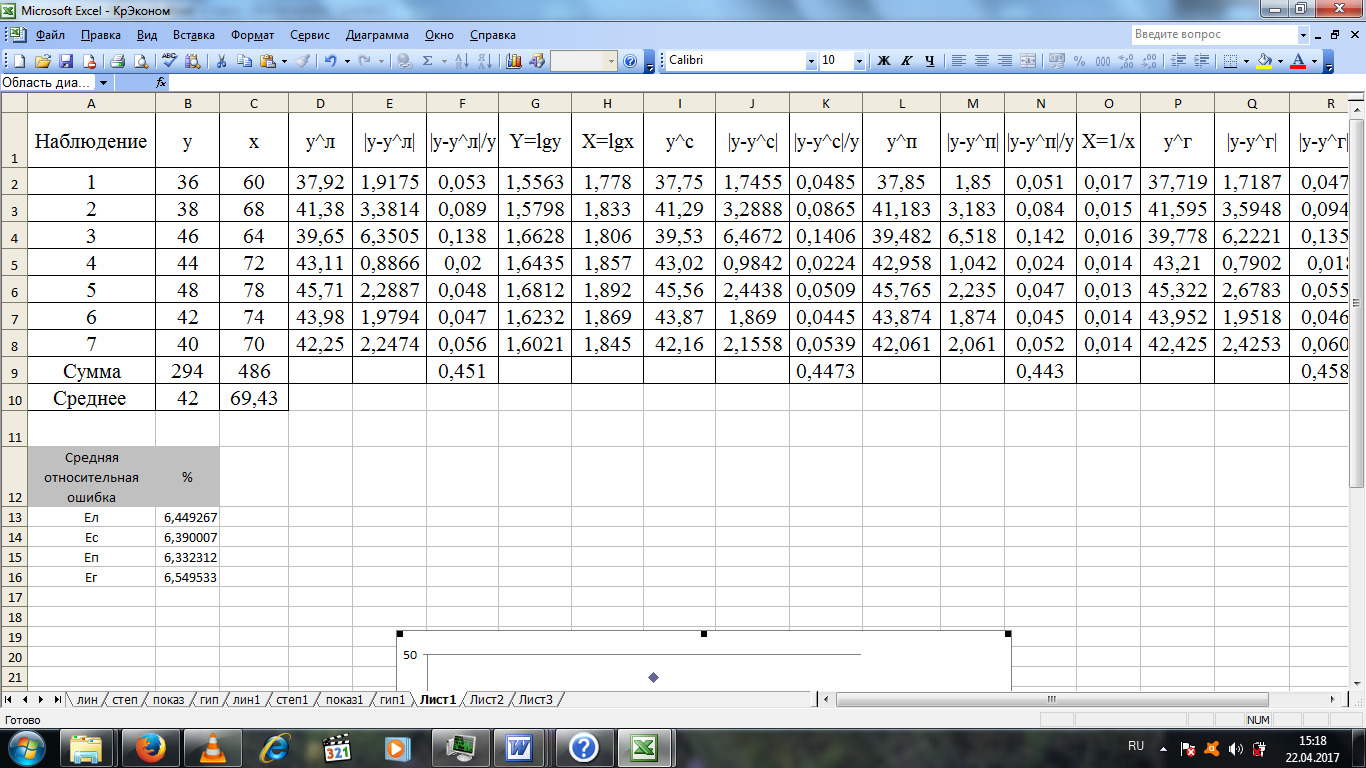
|
|
|
12 |


