Понятие статистической гипотезы. Процедура проверки статистической гипотезы.

Введение

Проверка гипотезы осуществляется на основе выявления согласованности эмпирических данных с гипотетическими (теоретическими). Если расхождение между сравниваемыми величинами не выходит за пределы случайных ошибок, гипотезу принимают. При этом не делается никаких заключений о правильности самой гипотезы, речь идет лишь о согласованности сравниваемых данных.

Основой проверки статистических гипотез являются данные случайных выборок. При этом безразлично, оцениваются ли гипотезы в отношении реальной или гипотетической генеральной совокупности. Последнее открывает путь применения этого метода за пределами собственно выборки: при анализе результатов эксперимента, данных сплошного наблюдения, но малой численности. В этом случае рекомендуется проверить, не вызвана ли установленная закономерность стечением случайных обстоятельств, насколько она характерна для того комплекса условий, в которых находится изучаемая совокупность.

Особенно часто процедура проверки статистических гипотез применяется для оценки существенности расхождений сводных характеристик отдельных совокупностей (групп): средних, относительных величин. Такого рода задачи, как правило, возникают в социальной статистике. Трудоемкость статистико-социологических исследований приводит к тому, что почти все они строятся на сплошном учете. Поэтому проблема доказательности выводов в социальной статистике стоит особенно остро. Применяя процедуру проверки статистических гипотез, следует помнить, что она может гарантировать результаты с определенной вероятностью лишь по «беспристрастным» выборкам, на основе объективных данных.

 

Понятие статистической гипотезы. Процедура проверки статистической гипотезы.

 

Статистической гипотезой называется предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки. Обозначается гипотеза буквой Н от латинского слова hypothesis. Так, может быть выдвинута гипотеза о том, что средняя в генеральной совокупности равна некоторой величине Н: μ = а, или о том, что генеральная средняя больше некоторой величины Н: μ > b.

Различают простые и сложные гипотезы.

Гипотеза называется простой, если она однозначно характеризует параметр распределения случайной величины.

Например, Н: μ = а. Сложная гипотеза состоит из конечного или бесконечного числа простых гипотез, при этом указывается некоторая область вероятных значений параметра.

Например, Н: μ > b. Эта гипотеза состоит из множества простых гипотез Н:μ = с, где с — любое число, большее b. Гипотезы о параметрах генеральной совокупности называются параметрическими, о распределениях - непараметрическими.

Гипотеза о том, что две совокупности, сравниваемые по одному или нескольким признакам, не отличаются, называется нулевой гипотезой (или нуль-гипотезой). Она обозначается Н_0. При этом предполагается, что действительное различие сравниваемых величин равно нулю, а выявленное по данным отличие от нуля носит случайный характер.

Например, Н₀: μ₁ = μ₂. Нулевая гипотеза отвергается тогда, когда по выборке получается результат, который при истинности выдвинутой нулевой гипотезы маловероятен. Границей не возможного или маловероятного обычно считают α = 0,05, т.е. 5%, или 0,01, 0,001. Если ориентироваться на правило «трех сигм», то вероятность ошибки α должна быть равна 0,0027. Однако для этого уровня вероятности ошибки значения критериев редко табулируются: как правило, значения критериев в статистико-математических таблицах рассчитаны для вероятностей ошибки 0,05; 0,01; 0,001.

Статистическим критерием называют определенное правило, устанавливающее условия, при которых проверяемую нулевую гипотезу следует либо отклонить, либо не отклонить. Критерий проверки статистической гипотезы определяет, противоречит ли выдвинутая гипотеза фактическим данным или нет.

Проверка статистических гипотез складывается из следующих этапов:

- формулируется в виде статистической гипотезы задача исследования;

- выбирается статистическая характеристика гипотезы;

- выбираются испытуемая и альтернативная гипотезы на основе анализа возможных ошибочных решений и их последствий;

- определяются область допустимых значений, критическая область, а также критическое значение статистического критерия (t, F,χ²) по соответствующей таблице;

- вычисляется фактическое значение статистического критерия;

- проверяется испытуемая гипотеза на основе сравнения фактического и критического значений критерия, и в зависимости от результатов проверки гипотеза либо отклоняется, либо не отклоняется.

При проверке гипотез по одному из критериев возможны два ошибочных решения:

1) неправильное отклонение нулевой гипотезы: ошибка 1-го рода;

2) неправильное принятие нулевой гипотезы: ошибка 2-го рода. В то время, как фактически нулевая гипотеза верна и нулевая гипотеза не верна, принимают два ошибочных решения: нулевая гипотеза отклоняется и принимается альтернативная гипотеза; нулевая гипотеза не отклоняется. Возможные решения представлены в табл.1

 

Возможные выводы при проверке гипотез

Решение	Фактически
по критерию	H0 верна	H0 не верна
H0 отклоняется	Ошибка 1-го рода	Правильное решение
H0 не отклоняется	Правильное решение	Ошибка 2-го рода

Таблица 1

Если, например, установлено, что новое минеральное удобрение лучше, хотя на самом деле его действие не отличается от старого, то это ошибка 1-го рода. Если мы решили, что оба вида удобрений одинаковы, то допущена ошибка 2-го рода.

Вероятности, соответствующие неверным решениям, называются риском 1 и риском 2. Риск 1 равен вероятности ошибки а (уровню значимости), риск 2 равен вероятности ошибки р. Поскольку а всегда больше нуля, то всегда есть риск ошибки β. При заданных α и объеме выборки значение β будет тем больше, чем меньше принятое α. Если велико, то α и β могут быть сколь угодно малыми, т.е. решения будут более обоснованными. При малом объеме выборки и малом а возможность установить фактически существующие различия мала. Обычно задают значение а и пытаются сделать возможно β малым. Вероятность 1 - β называется мощностью критерия: чем она больше, тем меньше вероятность ошибки второго рода.

Альтернативная гипотеза Н₁ может быть сформулирована по-разному в зависимости от того, какие отклонения от гипотетической величины нас особенно беспокоят: положительные, отрицательные либо и те, и другие. Соответственно альтернативные гипотезы могут быть записаны как

.

От того, как формулируется альтернативная гипотеза, зависят границы критической области и области допустимых значений.

Критической областью называется область, попадание значения статистического критерия в которую приводит к отклонению Н₀. Вероятность попадания значения критерия в эту область равна принятому уровню значимости. Область допустимых значений дополняет критическую область. Если значение критерия попадает в область допустимых значений, это свидетельствует о том, что выдвинутая гипотеза Нц не противоречит фактическим данным (H₀ не отклоняется). Точки, разделяющие критическую область и область допустимых значений, называются критическими точками или границами критической области. В зависимости от формулировки альтернативной гипотезы критическая область может быть двухсторонняя или односторонняя (левосторонняя либо правосторонняя). Если вычисляемое значение критерия попадает в критическую область, нулевая гипотеза отклоняется, она противоречит фактическим данным.

 

Задача №1.

1. Рассчитайте матрицу парных коэффициентов корреляции; оцените статистическую значимость коэффициентов корреляции.

2. Постройте поле корреляции результативного признака и наиболее тесно связанного с ним фактора.

3. Рассчитайте параметры линейной парной регрессии от ведущего фактора.

4. Оцените качество уравнения парной регрессии через коэффициент детерминации, среднюю ошибку аппроксимации и F-критерий Фишера.

5. Осуществите прогнозирование среднего значения показателя при уровне значимости , если прогнозное значения фактора составит 80% от его максимального значения. Представьте графически: фактические и модельные значения, точки прогноза.

По тринадцати коммерческим банкам имеются данные, характеризующие зависимость годовой прибыли от размера собственного капитала, общей суммы привлеченных средств и среднегодовых ставок по рублевым депозитам и краткосрочным кредитам:

1. Введите исходные данные в MS Excel.

№ банка	Прибыль (млн. руб.)	Собственный капитал (млн. руб.)	Привлеченные средства (млн. руб.)	Депозитная ставка (% годовых)	Кредитная ставка (% годовых)
				12,5	17,7
				11,7	18,2
				11,2	19,1
				9,7	15,2
				13,5	18,5
				10,8	18,6
				12,1	15,7
				11,7	16,6
				13,7	17,3
				12,5	19,3
				12,8	17,8
				11,2	14,5
				10,4	13,7

 

 

Матрицу парных коэффициентов корреляции можно рассчитать, используя инструмент Анализа данных Корреляция. Для этого:

 

2. В главном меню выбрать Сервис->Анализ данных->Корреляция

Заполнить диалоговое окно ввода параметров, в качестве входного интервала следует указать весь диапазон представленных данных

Результаты построения матрицы коэффициентов парной корреляции

Коэффициент парной корреляции между прибылью банка и величиной собственного капитала имеет положительную величину, следовательно, между этими признаками имеет место прямая связь, т.е. при увеличении величины собственного капитала прибыль банка увеличится, и такая же связь просматривается между прибылью банка и величиной привлеченных средств.

Коэффициент парной корреляции между прибылью банка и величиной депозитной, кредитной ставками имеет отрицательную величину, следовательно, между этими признаками имеет место обратная связь, т.е. при увеличении депозитной и кредитной ставки прибыль предприятия уменьшается.

Значения коэффициентов парной корреляции между факторными признаками, взятые по модулю, меньше величины 0,8, то явление мультиколлинеарности отсутствует, и, следовательно, все факторные признаки можно включать в модель множественной регрессии.

Для построения модели парной регрессии в главном меню выберите Сервис->Анализ данных->Регрессия

Заполните диалоговое окно ввода данных и параметров вывода

 

Результаты регрессионного анализа представлены

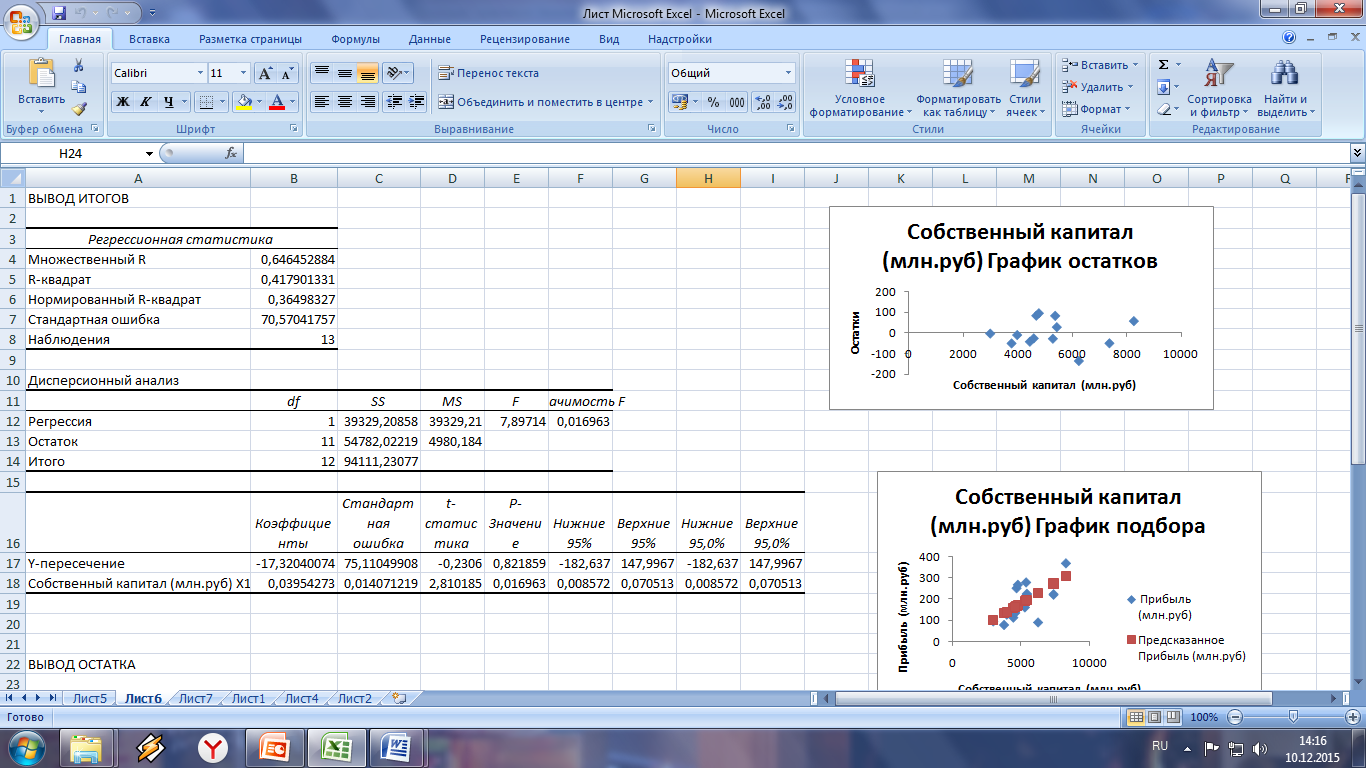
На основании этого можно записать уравнение линейной парной регрессии:

Y=-17.32+0.03*x

X= 0.8*8254=6603

Y= -17.32+0.03*6603=180.78

Оценим качество построенной модели множественной регрессии по следующим направлениям:

Коэффициент детерминации 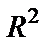= 0.417901331, следовательно, качество модели можно признать высоким.

Критерий Фишера F = 7.89714> Fтабл = 3.837853355, следовательно, уравнение регрессии признается статистически значимым.

12	Поделиться:

Воспользуйтесь поиском по сайту: