Задача 2. Построение модели множественной регрессии

 

1. Осуществите анализ матрицы парных корреляций на предмет мультиколлинеарности.

2. Используя пошаговую множественную регрессию (метод исключения или метод включения), постройте модель множественной регрессии. Дайте экономическую интерпретацию коэффициентов модели регрессии.

3. Оцените качество построенной модели. Улучшилось ли качество модели по сравнению с однофакторной моделью? Дайте оценку влияния значимых факторов на результат с помощью коэффициентов эластичности, b - и D - коэффициентов.

4. Постройте(по лучшей модели) прогноз результативного признака, если предположить, что значения факторных признаков увеличатся относительно средних значений на 10 %.

5. Внесите рекомендации по совершенствованию управления процессом (организацией).

По тринадцати коммерческим банкам имеются данные, характеризующие зависимость годовой прибыли от размера собственного капитала, общей суммы привлеченных средств и среднегодовых ставок по рублевым депозитам и краткосрочным кредитам:

 

№ банка	Прибыль (млн. руб.)	Собственный капитал (млн. руб.)	Привлеченные средства (млн. руб.)	Депозитная ставка (% годовых)	Кредитная ставка (% годовых)
				12,5	17,7
				11,7	18,2
				11,2	19,1
				9,7	15,2
				13,5	18,5
				10,8	18,6
				12,1	15,7
				11,7	16,6
				13,7	17,3
				12,5	19,3
				12,8	17,8
				11,2	14,5
				10,4	13,7

 

Решение

Введем данные в Excel

 

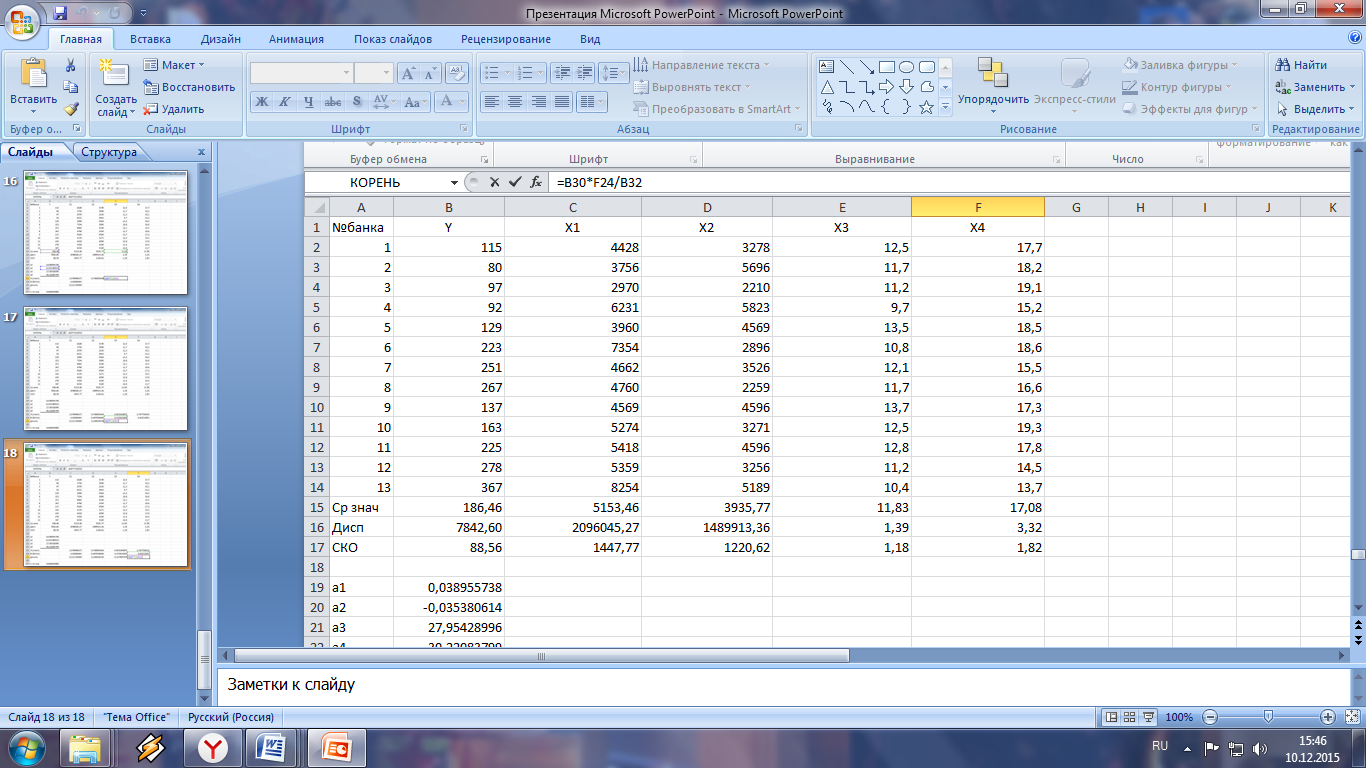
Для выявления явления мультиколлинеарности необходимо проанализировать коэффициенты парной корреляции между факторными признаками.

Факторные признаки, взятые по модулю, меньше величины 0,8, значит мультиколлинеарность отсутствует, и, следовательно, все факторные признаки можно включать в модель множественной регрессии.

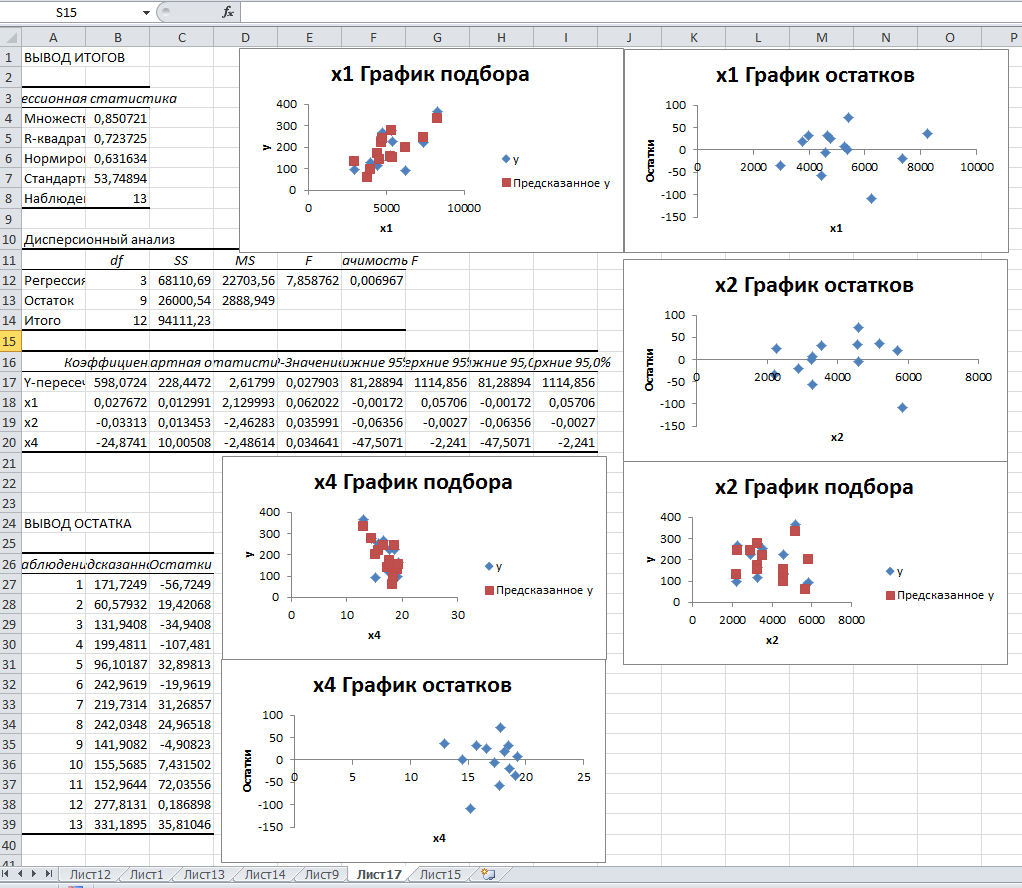
С помощью инструмента анализа данных Регрессия,помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности.

 

 

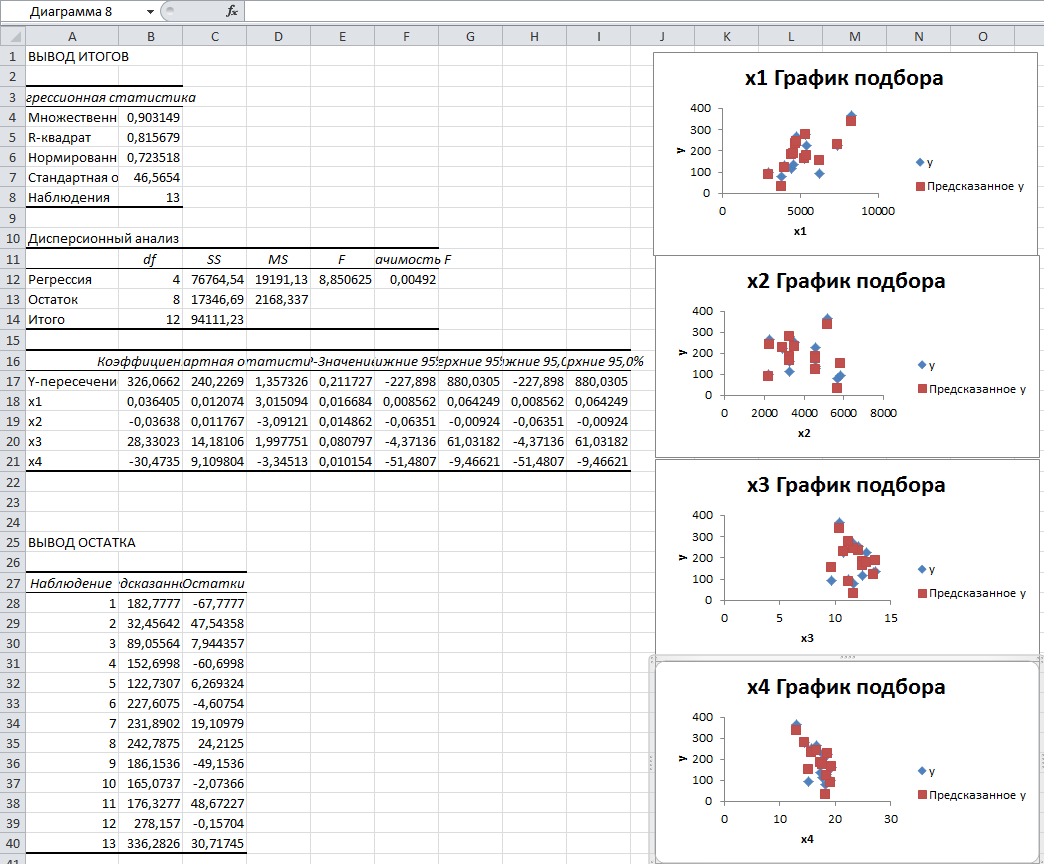
На основании полученных данных можно записать уравнение множественной регрессии

326+0,03*Х1-0,03*Х2+28,33*Х3-30,47*Х4

Оценим качество построенной модели множественной регрессии по следующим направлениям:

Коэффициент детерминации 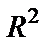= 0,815679 достаточно близок к 1, следовательно, качество модели можно признать высоким.

Для определения критерия Фишера:

 

 

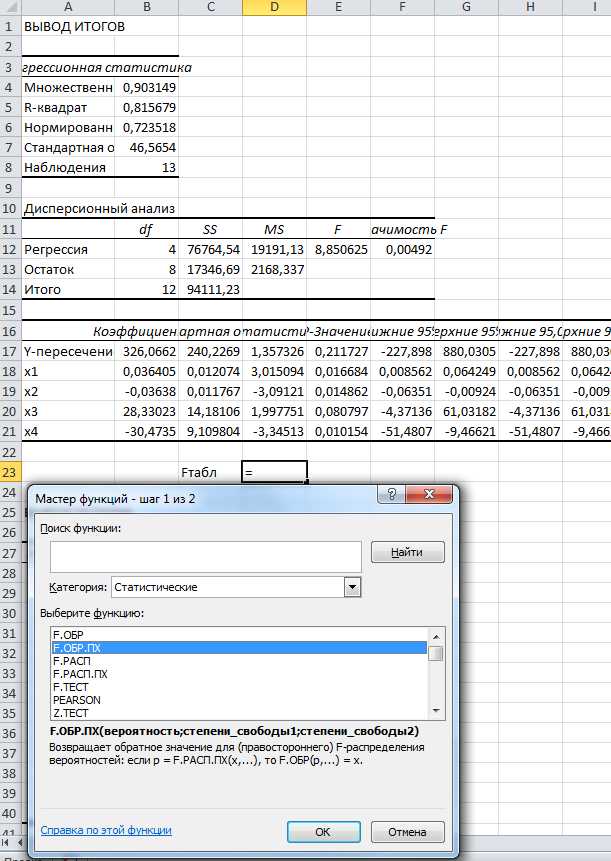
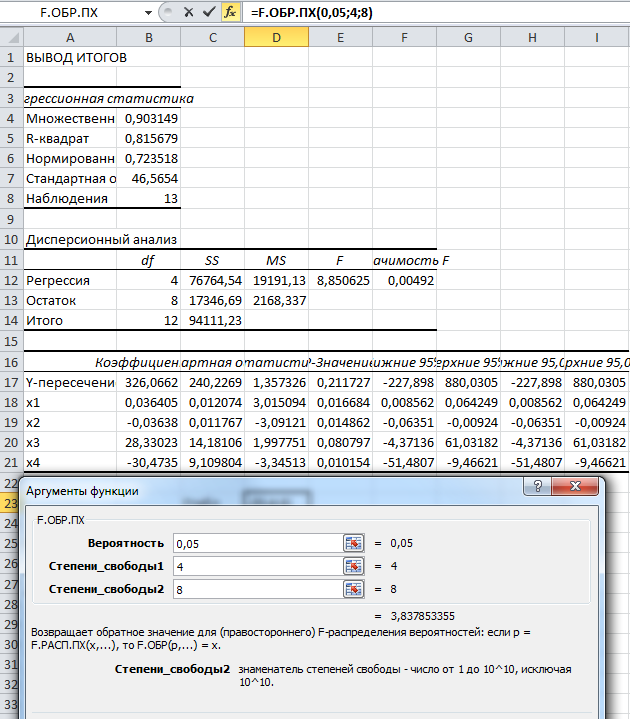
Fтабл=3,837853355

Сравнивая Fтабл и Fпракт строим новую регрессию без х3

 

 

Для определения критерия Стьюдента:

 

 

 

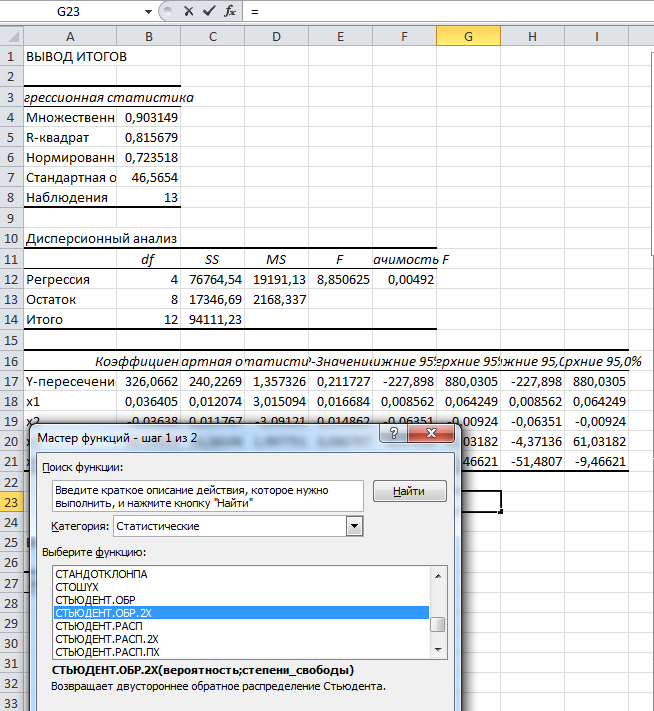
Tтабл=2,306004135

Оценим качество построенной модели множественной регрессии с помощью коэффициентов эластичности, b - и D - коэффициентов.

Коэффициент эластичности определяется:

,

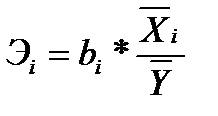где - среднее значение соответствующего факторного признака,

- среднее значение результативного признака.

b_i – коэффициенты регрессии соответствующих факторных признаков.

ß-коэффициент определяется по следующей формуле:

,

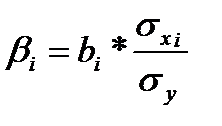где 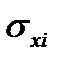- среднеквадратическое отклонение (СКО) соответствующего факторного признака (рассчитывается как корень квадратный из дисперсии признака),

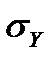- СКО результативного признака.

∆-коэффициент определяется по следующей формуле:

,

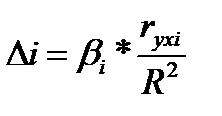Найдем среднее значение

Найдем дисперсию

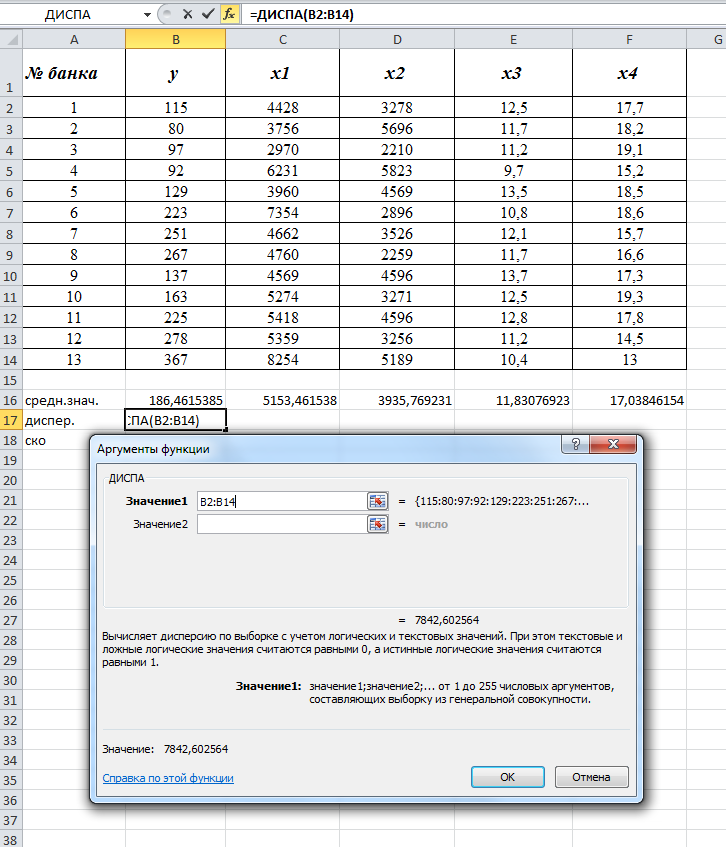
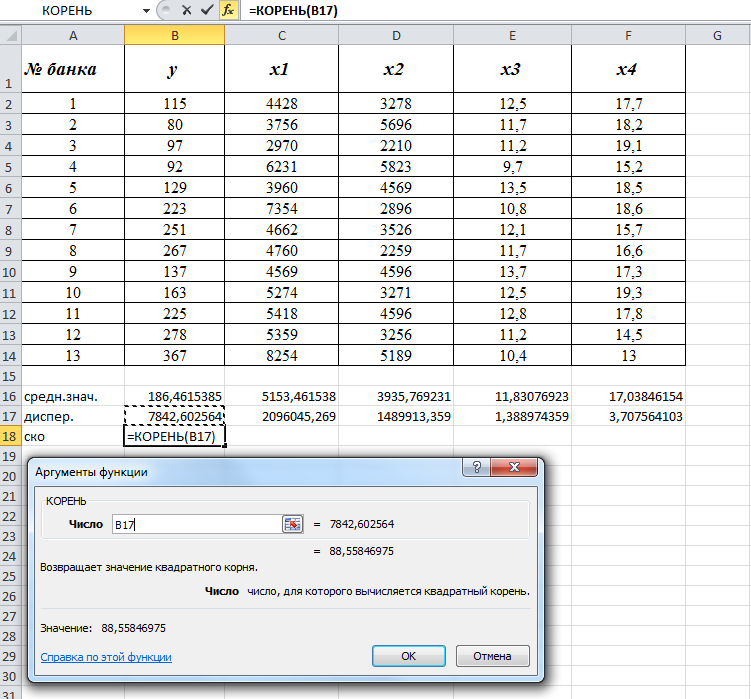
Найдем СКО

Расчеты описанных выше коэффициентов

 

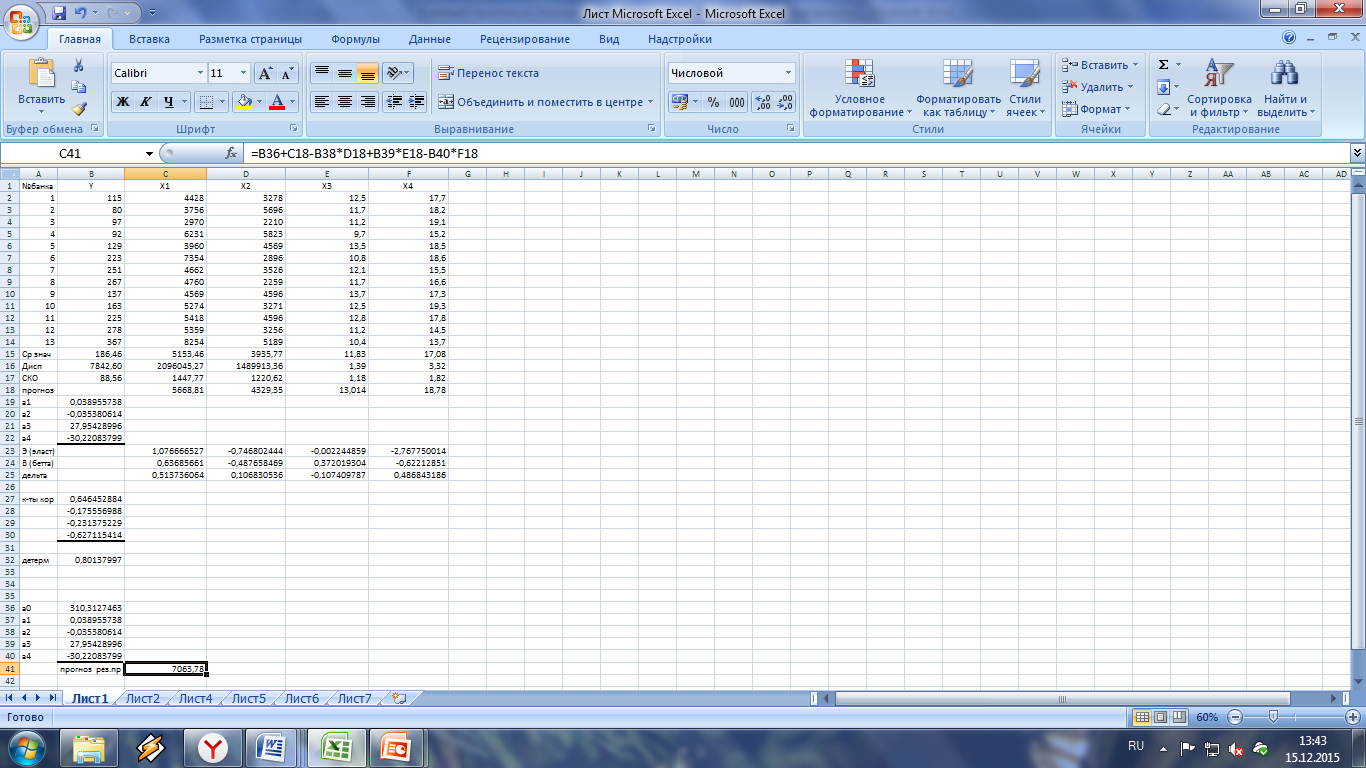
Таким образом, прогнозное значение прибыли кредитных организаций
Y_прогн=7063,78

Уравнение регрессии признано статистически значимым по критерию Фишера и обладает достаточно высоким качеством, следовательно, результаты расчетов можно признать надежными и достоверными.

 

 

Список использованной литературы

1. Общая теория статистики: учебник. Под ред. Елисеевой И.И.2012

2. Основы статистического анализа. Практ. по стат. мет. и исслед. операций с исп. пакетов STATISTICA и EXCEL: Уч.пос./ Э.А.Вуколов - 2 изд., испр. и доп. - М.: Форум:НИЦ Инфра-М, 2013.

3. Эконометрика: теоретические основы: Учебное пособие / Г.А. Соколов. - М.: ИНФРА-М, 2012.

4. Валентинов, В. А. Эконометрика [Электронный ресурс]: Практикум / В. А. Валентинов. - 3-е изд. - М.: Дашков и К, 2010.

5. Методы и средства научных исследований: Учебник/А.А.Пижурин, А.А.Пижурин (мл.), В.Е.Пятков - М.: НИЦ ИНФРА-М, 2015.

6. Уткин, В. Б. Эконометрика [Электронный ресурс]: Учебник / В. Б. Уткин; Под ред. проф. В. Б. Уткина. - 2-е изд. - М.: Издательско-торговая корпорация «Дашков и К°», 2012.

7. Математические методы в современных социальных науках: Уч. пос./ Г.В. Осипов, В.А. Лисичкин; Под общ. ред. В.А. Садовничего. - М.: Норма: ИНФРА-М, 2014.

8. Березинец, И. В. Основы эконометрики: Учеб. пособие / И. В. Березинец; Высшая школа менеджмента СПбГУ. — 4-е изд., испр. и доп. — СПб.: Изд-во «Высшая школа менеджмента», 2011.

 

 

12	Поделиться:

Воспользуйтесь поиском по сайту: