Измерение частотно-контрастной характеристики тепловизора

 

1. Цель работы

 

1.1 Изучение устройства тепловизора и получение практических навыков работы с ним.

1.2 Измерение Функции Передачи Модуляции (ФПМ) тепловизора.

 

2. Домашнее задание

 

2.1 Изучить принцип работы тепловизора и взаимодействие его блоков.

2.2 Определить длину волны, на которую приходится максимум излучательной способности абсолютно черного тела (АЧТ) при температуре 25° С и 35°С.

2.3 Рассчитать мгновенное поле зрения для тепловизора на расстоянии 0.5, 1 и 2м, если разрешающая способность тепловизора 1 мрад.

2.4 Рассчитать теоретическую ФПМ прибора с дифракционно ограниченным объективом и светоприемной матрицей.

 

 

3. Задание, выполняемое в лаборатории

 

3.1 Ознакомиться с инструкцией по эксплуатации и подготовить тепловизор к работе.

3.2 Определить температуру окружающей среды с помощью контактного термометра.

3.3 Установить температуру АЧТ на 40˚С больше температуры окружающей среды.

3.4 Поместить перед АЧТ регулируемую щель и произвести запоминание термогарммы (см. п.1 указаний по выполнению работы).

3.5 Вместо черного тела и щели установить перед тепловизором на том же расстоянии оптическую миру №7. Провести нагревание миры галогенной лампой. Запомнить термограмму после того, как изображение миры станет достаточно контрастным.

3.6 Установить квадрат миры, соответствующий предельному разрешению тепловизора. Получить несколько термограмм, помещая квадрат миры с предельным разрешением в периферическую область поля зрения.

3.7* В предположении, что система линейна выделить переходную кривую из полученных с помощью АЧТ и щели термограмм, по ним рассчитать функцию рассеяния линии. С помощью Фурье - преобразования полученной линии рассеяния получить ФПМ тепловизора.

3.8 Используя термограмму нагретой миры получить ФПМ тепловизора и сравнить ее с полученной в п. 3.7.

3.9 Сравнить полученные передаточные характеристики тепловизора, сделать выводы и оформить отчет по работе.

 

4. Описание лабораторной установки

Лабораторная установка содержит тепловизор NEC, планарное абсолютно черное тело, регулируемую щель, штатив для тепловизора и оптическую миру №7.

Источником инфракрасного излучения служит галогенная лампа мощностью 500Вт.

5. Методические указания

5.1 Общие указания

 

Перед выполнением измерений следует ознакомиться и руководством по эксплуатации пирометра и тепловизора.

Ввиду большой чувствительности тепловизора к флуктуациям теплового излучения (до 0.1ºС) при проведении измерений температуры следует обратить внимание не следующие источники погрешности:

Состояние поверхности контролируемого объекта сильнее других факторов влияет на результаты измерения, и этот фактор следует считать основным при использовании тепловизора. Поэтому поверхность контролируемого объекта должна быть очищена от загрязнений и пыли.

Тепловое излучение от посторонних источников тепла (батареи отопления, лампы, паяльники и т.п.) не должно прямо или однократно отразившись попадать в объектив тепловизора.

 

5.2 Типовое устройство современного телповизора

 

Тепловизионные приборы предназначены для наблюдения объектов по их собственному излучению. Принцип действия приборов этого типа основан на преобразовании излучения инфракрасного (ИК) диапазона в видимый диапазон длин волн излучения. Спектральный диапазон, в котором работают тепловизоры, определяется интервалами длин волн в области максимума энергии излучения наблюдаемых объектов в соответствующих окнах прозрачности атмосферы. Обычно это интервалы длин волн от 3,5 до 5,5 мкм или от 8 до 13,5 мкм. Современные тепловизоры позволяют обнаруживать объекты, имеющие температурные контрасты до десятых и даже сотых долей градусов, формируют изображение в телевизионном или близком к телевизионному стандартах и находят, в связи с этим широкое применение в промышленности, медицине и военном деле.

В качестве приемника излучения используются матричные приемники излучения, так называемые фокальные матрицы, работающие в режиме накопления зарядов и основанные на различных физических принципах.

На рис. 5.1 представлена обобщенная функциональная схема тепловизора с фокальной ИК матрицей.

Типовые фокальные ИК матрицы могут иметь размерность 128х128, 256х256, 512х512 и более элементов (необязательно с равным соотношением по вертикали и горизонтали) при размере этих чувствительных элементов 30х30 мкм². Фокальные матрицы изготавливаются как функционально законченные фотоприемные устройства (ФПУ), включающие систему охлаждения, предусилители, мультиплексор, корректор неоднородности характеристик чувствительных элементов, аналого-цифровой преобразователь, блоки цифровой обработки и формирователь выходных сигналов. Сигналы с выхода такого ФПУ могут передаваться на видеоконтрольное устройство (ВКУ) телевизионного типа либо в цифровом виде в блоки цифровой обработки.

 

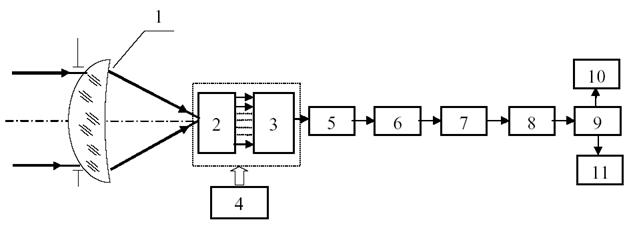
Рис. 4.1 Обобщенная функциональная схема тепловизора с фокальной

матрицей: 1 – оптическая система; 2 – фокальная матрица с предусилителями; 3 –

мультиплексор; 4 – система охлаждения; 5 – корректор неоднородности

характеристик чувствительных элементов; 6 – аналого-цифровой преобразователь;

7 – цифровой корректор неоднородности; 8 – корректор неработающи ячеек; 9 –

формирователь изображения; 10 – дисплей; 11 – цифровой выход.

 

 

5.3 Указания по выполнению домашнего задания

При изучении теоретических вопросов обратить внимание на то, какие величины влияют на поток теплового излучения и показания тепловизора при измерении температуры.

Максимум температуры АЧТ соответствует длине волны (в мкм)

λmax= 2898 / Т,

где Т- абсолютная температура АЧТ в К.

Диапазон длин волн, воспринимаемых тепловизором составляет 8-14 мкм.

Для расчета ФПМ дифракционно ограниченного объектива для монохроматического света воспользоваться формулой (5.1). При этом принять длину волны равной максимуму излучения АЧТ при температуре 25ºС, входной зрачок объектива тепловизора 60мм, фокусное расстояние 40мм.

(5.1)

где f – фокусное расстояние объектива;

D – входной зрачок объектива;

λ – длина волны;

ν – пространственная частота.

ФПМ матрицы с дискетным количеством элементов рассчитывается:

(5.2)

Где dx – шаг между светочувствительными элементами. Принять с шаг между пикселями 50 мкм.

Суммарную ОПФ рассчитать как произведение функций отдельных звеньев.

 

5.4 Общие сведения о частотно-контрастных характеристиках изображающих систем

 

Для оценки качества изображения в настоящее время широко используют такие характеристики как разрешающая способ­ность, частотно-контрастная характеристика, функция раз­мытия точки или линии и другие [1]. В соответствии с этой теорией всякий объект может быть представлен как совокупность точек различной яркости, а каждая нагретая точка пре­вращается тепловизионным устройством в дифракционное пятно, происходит наложение этих пятен друг на друга, в результате чего изображение размывается, мелкие детали исчезают, т. е. перестают разрешаться. Для нахождения этой характеристики используют пространственные тест-объекты (миры) различ­ных типов: штриховые линейные миры, радиаль­ные миры, миры с синусоидальным распределением яркости и другие специальные тест-объекты самой различной формы. Весьма распространенным является определение разрешающей способностипо наибольшему числу линий штриховой миры, отдельные элементы изображения которой еще можно видеть раздельно. Однако найденное значение сильно зависит от формы и особенно от контраста между элементами тест-объекта, от характеристик устройства, с помощью которого рассматривается оцениваемое изображение, от свойств наблю­дателя, от выбранной методики и условий проведения испы­таний и т. д.

Указанные характеристики позволяют оценить несоответ­ствие воспроизводимого изображения входному по двум ка­налам: 1) фильтрации пространственной частоты и 2) флуктуационным помехам — зернистости.

Для изучения искажения изображения, вносимой тепловизионной системой в настоящее время широко применяется аппарат передаточных функций.

Рассмотрим иска­жение тепловизионной системой пространственной часто­ты ν, под которой понимается величина, обратная обычной длине периода линейной миры, т. е. равная числу периодов пространственной решетки в единице длины. Излу­чение любого объекта всегда можно рассматривать как супер­позицию системы пространственных синусоидальных волн, каждая составляющая которой характеризуется своей ампли­тудой, пространственной частотой и фазой [1].

В лабораторной работе предлагается использовать понятия и методы теории линейных систем в решение задачи о нахождении функции, характеризующей свойства изображающей системы. Предмет можно рассматри­вать в виде совокупности светящихся элементарных объектов (точек, линий, полуплоскостей). Если совокупность этих со­ставляющих эквивалентна предмету и изображающая система линейная, то изображение предмета можно получить сумми­рованием (суперпозицией) изображений элементарных объ­ектов. Требование линейности нарушается лишь в том случае, когда заметную роль начинают играть процессы взаимодействия одних лучей света с другими: явление нелинейной оптики, рассеяние фотонов на фотонах, интерференция.

Пусть рассматриваемый предмет характеризуется распре­делением светимости в виде функции Е(х', у'). Будем счи­тать, что координаты х', у' характеризуют предметную пло­скость, а х, у — плоскость изображения. Система воспроизве­дения передает каждую точку предмета в виде пятна рассеян­ной энергии, так что описывающая его функция а(х, у) будет отлична от нуля в конечной области значений х и у. Оконча­тельную картину можно построить, если идеальное изображе­ние разбить на бесконечно малые элементы d х' dy', а затем каждый из них заменить изображением соответствующей точки объекта, которое задается функцией а(х, у). Реальные изображения отдельных точек предмета налагаются друг на друга, вследствие чего результирующая освещенность Е(х, у) является результатом их суперпозиции. Такая операция соответствует свертке функций, приложенная к закону излучения данного объекта Е(х', у') и к закону распределения света в изобра­жении точки а(х, у):

причем осуществляется нормировка:

Таким образом, а(х, у) позволяет рассчитывать освещен­ность в изображении любого объекта, если известно распре­деление его светимости. Функция а(х, у) характеризует свой­ства системы воспроизведения и называется функцией размы­тия точки (откликом на импульсное возбуждение, аппаратной функцией).

Для идеального устройства а(х, у) везде, кроме точки x = 0, y = 0, равна нулю.

В тех случаях, когда в изучаемых объектах светимость меняется в одном направлении, например вдоль оси х, их можно рассматривать состоящими из бесконечно узких прямо­линейных источников, параллельных оси у. Тогда

В этом случае функция а(х) физически выражает распределение энергии в изображении данной системой бесконечно узкого источника (линии), параллельного оси у. Она называется функцией размытия линии и также широко применяется для оценки воспроизводящих уст­ройств.

Описанные выше зависимости можно использовать для изучения свойств реальной воспроизводящей линейной систе­мы, связанных с ее отличием от идеальной. В общем случае эти свойства можно характеризовать с помощью функции, задающей распределение освещенности в изображении ка­кого-нибудь стандартного тест-объекта с определенным рас­пределением светимости. Если, например, взять точечный источник, то рассматриваемое воспроизводящее устройство характеризуется функцией размытия точки, если бесконечно узкий прямолинейный источник — функцией размытия линии, если полуплоскость — переходной функцией (пограничной кривой системы, откликом на единичный скачок).

Большинство исследователей отдают предпочтение анализу изображающих систем с помощью пространственно частотных характеристик (такое название выбрано по аналогии с частотными характеристиками в теории связи). Их еще назы­вают функциями передачи модуляции, частотно-контрастными характеристиками, апертурными характеристиками, функция­ми реакции, линейными частотными реакциями, коэффициен­тами передачи контраста и т. д. Они описывают качество систем в терминах контраста изображения периодических тест-объектов различной пространственной частоты:

(5.3)

где E_max, E_min — максимальная и минимальная освещённости изображения, полученного тепловизором,

L_max L_min — максимальная и минимальная яркости оригинала.

Дело в том, что при этом отно­шение контраста изображения решетки k (ν) к контрасту самой решетки к₀ (ν) не зависит от контраста последней.

Отношение k (ν) / к₀ (ν) определяет пространственную частотную характеристику Т (ν).

Часто вместо функции рассеяния линии применяются такие понятия, как пограничная кривая I(х), функция контрастности светлой полоски С(b) или темной полоски С'(b) ширины b.

Пограничная кривая показывает распределение освещен­ности в изображении резкой прямолинейной границы свет — тень и связана с а(х) дифференциальным соотно­шением:

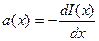(5.4)

Пространственная частотная характеристика и функция рассеяния точки а(х) связанны между собой прямым и обратным преобразованием Фурье [1].

(5.5)

 

(5.6)

Выражение (5.3) можно записать в виде:

(5.7)

Величина T(ν) и называется функцией передачи модуляции или частотно контрастной характеристикой (ЧКХ).

Итак, качество изображающей системы характеризуется близостью изображения к оригиналу, их сходством. Близость изображения можно рассматривать для простых объектов, таких как точка, линия, полуплоскость, но удобнее оперировать преобразованиями Фурье этих объектов, рассматривая передачу системой синусоидальных составляющих с различными пространственными частотами. Изменение амплитудной составляющей в изображении для разных пространственных частот характеризуется функцией передачи модуляции, или ее называют частотно-контрастной характеристикой.

 

5.5 Указания к выполнению лабораторного задания

 

5.5.1 Щель должна располагаться по возможности ближе к АЧТ (для попадания в зону резкого изображения тепловизора). Тепловизор следует расположить на расстоянии 1м от АЧТ. Фокусировку можно провести до получения четкого изображения щели и АЧТ. Ширина щели должна быть выбрана таким образом, чтобы в середине отверстия щели на экране тепловизора наблюдалась температура, как можно близкая к температуре АЧТ (или соответствующая ей световая градация). После выполнения всех условий провести запоминание термограммы на компьютере. Для расчета функции передачи модуляции необходимо будет знать температуры неискаженного изображения. Для этого измерить их можно с помощью контактного датчика – температуру АЧТ и температуру массивной части щели.

5.5.2 Для расчета передаточной функции тепловизора по термограмме миры так же потребуется узнать ее температуру. Нагрев миры производить до получения на термограмме изображений с наибольшей пространственной частотой. В связи с кратковременной экспозицией миры для нагрева, для получения температуры белого и темного участков миры, которые следует принять постоянными по всей ее площади рекомендуется воспользоваться пирометром. Для этого предварительно ввести поправку на излучательную способность темной и светлой частей миры при комнатной температуре с помощью контактного датчика.

 

5.6 Указания по расчету частотно-контрастной характеристики тепловизора с помощью пограничной кривой

 

Для получения ЧКХ изображающей системы тепловизора воспользуемся термограммами, полученными с помощью щели и АЧТ, затем сравним их с ЧКХ, полученными с помощью миры №7.

Из температур по строке термограмм выделяется правая и левая часть относительно максимума. Выделенные фрагменты рассматриваются как пограничная функция. Как известно для получения функции размытия линии (реакции системы на дельта-функцию) необходимо продифференцировать пограничную кривую (2). ЧКХ получается Фурье-преобразованием ФРЛ. Итоговая ЧКХ для повышения достоверности следует получить осреднением нескольких импульсов. Для выделения группы пикселей, относящихся к переходной кривой можно использовать порядка 20 точек (пикселям) или выбрать их количество самостоятельно, по явному превалированию сигнала над шумами.

При расчете передаточной функции под температурами оригинала изображения понимается их температура, измеренная альтернативным методом – контактным в этом случае.

Для пересчета в пространство частот необходимо номер точки заменить на расстояние, с учетом шага между пикселями матрицы тепловизора NEC - 50мкм (сам пиксель при этом приблизительно в два раза меньше). То есть i- му пикселю будет соответствовать аргумент i *dx, где dx – шаг матрицы.

Рис 5.2 Изображение переходной кривой

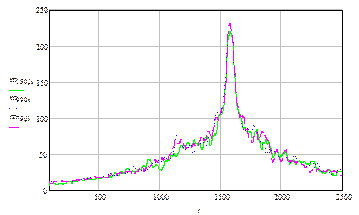Рис 5.3 Профиль яркости по строке изображения переходной кривой

 

5.7 Указания по расчету частотно-контрастной характеристики тепловизора с помощью миры.

Для расчета ФПМ необходимо оперировать контрастом а не яркостью (температурой). Контраст рассчитывается по формуле:

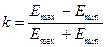(5.8)

где E_max и E_min — максимальные и минимальные значения температуры в исследуемом изображении.

Для определения коэффициента контрастности на конкретной пространственной частоте необходимо измерить амплитуду сигнала термограмм в двух точках, соответствующих черным и белым штрихам и определить его по формуле 4.1. Далее, получив контраст для нескольких пространственных частот, минимум для десяти – построить частотно-контрастную характеристику.

Выраженный таким образом контраст изображения (при применении стопроцентно контрастной решетки) численно равен коэффициенту передачи контраста данной системой.

Этот коэффициент показывает, во сколько раз изменяется контраст изображения решетки по сравнению с контрастом самой решетки. Выраженный таким образом коэффициент передачи контраста удобен тем, что его легко измерить.

Отметим, что данный метод измерения ФПМ имеет наибольшую точность, в связи с тем, что наименее подвержен влиянию шумов и юстировок оптической части установки.

Рис. 5.4 Распределение освещенности прямоугольной миры

 

Для расчета передаточной функции температуру оригинала изображения принять, полученную с помощью пирометра с поправкой на излучательную способность.

При измерениях так же необходимо учесть, что результаты были получены для решетки с прямоугольным распределением яркости (рис.4.4). Для перевода полученных значений к синусоидальным распределениям яркости контраст необходимо пересчитать по формуле Кольтмана (приведен только первый член ряда, что достаточно на практике):

ЧКХ_sin(ν)= (π/4) * ЧКХ (ν) (5.9)

В зарубежной литературе передаточная функция, полученная при прямоугольном распределении штрихов, часто называется функцией передачи контраста (Contrast Transfer Function CTF), в то время как функция передачи синусоидальных сигналов называется функцией передачи модуляции (Modulation Transfer Function).

MTF(ν)= (π/4) * CTF(ν) (5.10)

Полученные функции передачи модуляции привести на одном графике.

Ниже приведена таблица пространственных частот для миры ГОИ №7.

Номер элемента
Ширина полос, мкм
Число полос, мм	0.8	0.85	0.85	0.9	1.0	1.05	1.1	1.15	1.25
Номер элемента
Ширина полос, мкм
Число полос, мм	1.3	1.4	1.45	1.55	1.65	1.7	1.85	1.95	2.1
Номер элемента
Ширина полос, мкм
Число полос, мм	2.2	2.35	2.5	2.6	2.75	2.95

 

 

6. Контрольные вопросы

 

5. Каким образом происходит теплопередача?

6. От чего зависит теплопередача за счет теплопроводности и конвекции?

7. От чего зависит поток теплового излучения?

8. Назовите основные составляющие погрешности при измерении температуры тепловизором.

9. Как влияет состояние поверхности объекта на показания теполвизора и пирометра?

10. Что такое функция передачи модуляции?

11. Какие способы определения функции передачи модуляции вы знаете, какие из них наиболее точные?

 

Литература

 

1. Перрен Ф. Методы оценки фотографических систем // Успехи Физических наук. 1962, Т. LXXVII. с. 307-344.

1. Неразрушающий контроль: Справочнк: в 8 т. / Под общ. ред. В.В. Клюева. Том 5. Тепловой контроль. В.П. Вавилов. – 2-е изд.- М.: Машиностроение, 2006 – 688с.
2. Ермолов И.Н., Останин Ю.Я. Методы и средства неразрушающего контроля качества: Учеб. пособие для инженерно-техн. спец. вузов. – М.:Высш. шк., 1988 – 368с.

 

СОДЕРЖАНИЕ

 

1. Лабораторная работа № 1. Измерение формы объектов методом светового сечения………………………………………………….….……………….…..……… 3
2. Лабораторная работа № 2. Измерение функции передачи модуляции цифровой камеры……………………………………..………………………………………..……9
3. Лабораторная работа № 3. Визуально-оптический контроль с помощью стереомикроскопа………………………………………….…………….………..……17
4. Лабораторная работа № 4. Измерение температуры объектов бесконтактными способами……………………………………………………………………..……..….22
5. Лабораторная работа № 5. Измерение частотно-контрастной характеристики тепловизора…………………………………………………………………....……..…26

 

 

* Пункты 3.6, 3.7, 3.8 и 3.9 могут быть выполнены после завершения лабораторного занятия

* Пункты 3.7, 3.8 и 3.9 могут быть выполнены после завершения лабораторного занятия

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: