Главная | Обратная связь | Поможем написать вашу работу!

Лабораторная работа №2.

Стр 1 из 2Следующая ⇒

ПОСТРОЕНИЕ МОДЕЛИ ЛИНЕЙНОЙ ПАРНОЙ РЕГРЕССИИ

Лабораторная работа №1.

Вычисление коэффициентов уравнения линейной регрессии

Парная регрессия – это уравнение связи двух переменных у и х:

где y ‑ зависимая переменная (результативный признак); x ‑ независимая, объясняющая переменная (признак ‑ фактор).

Линейная парная регрессия: .

Построение уравнения регрессии сводится к оценке ее параметров (в приведенных выше уравнениях регрессии – параметры a и b). Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических минимальна, т.е.

Для линейных уравнений решается следующая система относительно a и b:

Для решения данной системы и нахождения a и b можно использовать два подхода:

1. Используются следующие соотношения:

, , ,

2. Можно воспользоваться готовыми формулами, которые вытекают из этой системы:

(1)

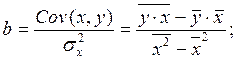(2)

где ‑ коэффициент выборочной ковариации; 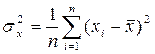‑ дисперсия факторного признака или выборочная вариация, обозначаемая как .

Задача

Исследуем зависимость между доходом (х) домохозяйства и его расходом на продукты питания (y). Выборочные данные по 40 домохозяйствам представлены в таблице 1.

Таблица 1

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.

2. Постройте линейное уравнение парной регрессии у от х.

Решение.

1. Для расчета параметров уравнения линейной регрессии постройте расчетную таблицу 2.

Таблица 2

№ дом.	Расходы на продукты питания (y), тыс. руб.	Доходы (х), тыс. руб.	xy	x²	y²
	14,5	25,5
	11,3	26,5
	14,7	27,2
	10,2	29,6
	13,5	35,7
	9,9	38,6
	12,4
	8,6	39,3
	10,3
	13,9	41,9
	14,9	42,5
	11,6	44,2
…	…	…
	27,3
Средние значения

2. Используя формулы 1, 2 рассчитайте параметры a и b.

3. Запишите полученной уравнение парной регрессии.

4. Для проверки правильности полученного уравнения воспользуйтесь статистической функцией ЛИНЕЙН табличного процессора Microsoft Excel, для этого:

− выделите интервал ячеек, содержащий 2 столбца и 5 строк;

− вставьте функцию ЛИНЕЙН, задайте значение константы и статистики равными единице.

− введите формулу как формулу массива, для чего нажмите клавишу F2 а затем комбинацию клавиш Ctrl+Shift+Enter.

В таблице 3. показано, в каком порядке возвращается дополнительная регрессионная статистика.

Таблица 3

b	a
se_b	se_a
r²	se_y
F	df
ss_рег.	ss_ост.

5. Используя полученное уравнение регрессии, определите ожидаемые расходы на продукты питание, если доходы составят: а) 21,2 тыс. руб. (интерполяция данных); б) 95,27 тыс. руб. (экстраполяция данных).

Лабораторная работа №2.

Вычисление коэффициента корреляции и средней ошибки аппроксимации

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции :

где , .

Линейный коэффициент корреляции изменяется в пределах .

Равенство коэффициента нулю свидетельствует об отсутствии линейной связи. Равенство коэффициента ‑1 или +1 показывает наличие функциональной связи. Знак «+» указывает на связь прямую (увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака), знак «‑» указывает на связь обратную (увеличение или уменьшение одного признака сопровождается противоположным по направлению изменением другого признака). Показателям тесноты связи можно дать качественную оценку:

Количественная мера тесноты связи	Качественная характеристика силы связи
до 0,25	Очень слабая
0,25 – 0,44	Слабая
0,45 – 0,64	Умеренная
0,65 – 0,80	Сильная
0,81 – 0,90	Весьма сильная
0,91 – 1,00	Очень сильная

Оценку качества построенной модели определяет коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.

Коэффициент детерминации :

Коэффициент детерминации принимает значения от 0, когда факторы x не оказывают никакого влияния на зависимую переменную, до 1, когда изменения зависимой переменной y полностью объяснимы влиянием факторов модели.

Функциональная связь возникает при значении равном 1, а отсутствие связи ‑ 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50%. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.

Средняя ошибка аппроксимации ‑ среднее отклонение расчетных значений от фактических:

Допустимый предел значений ‑ не более 8 ‑ 10%.

Задача

Определим линейный коэффициент парной корреляции и среднюю ошибку аппроксимации для уравнения парной регрессии, полученного в Лабораторной работе №1.

Решение.

1. Дополните таблицу 2. следующими расчетными полями (табл. 4).

Таблица 4

№ дом.	Расходы на продукты питания (y), тыс. руб.	Доходы (х), тыс. руб.	xy	x²	y²
	14,5	25,5
	11,3	26,5
	14,7	27,2
	10,2	29,6
	13,5	35,7
	9,9	38,6
	12,4
	8,6	39,3
	10,3
	13,9	41,9
	14,9	42,5
	11,6	44,2
….
	27,3
Итого
Средние значения

2. Сравните полученное значение коэффициента детерминации со значением, вычисленным функцией ЛИНЕЙН.

3. Сделайте выводы о тесноте связи и об оценке качества построенной модели.

12 Следующая ⇒

Воспользуйтесь поиском по сайту: