 |
Лабораторная работа №5.
|
|
|
|
Расчет доверительных интервалов
Заметим, что все оценки, приведенные ранее, определяются одним числом, т.е. являются точечными. При малых объемах выборки точечная оценка может приводить к большим ошибкам и значительно отличаться от оцениваемого параметра. Более широкое применение получил метод доверительных интервалов, разработанный американским статистиком Ю. Нейманом.
Таким образом, рассчитанные значения показателей (коэффициенты a, b, rxy) являются приближенными, полученными на основе имеющихся выборочных данных. Для оценки того, насколько точные значения показателей могут отличаться от рассчитанных, осуществляется построение доверительных интервалов. Доверительные интервалы определяют пределы, в которых лежат точные значения определяемых показателей с заданной степенью уверенности, соответствующей заданному уровню значимости a. При построении эконометрических регрессионных моделей доверительные интервалы обычно определяют для двух уровней значимости ‑ 
и 
. Соответственно говорят о 5-процентоном уровне значимости или об 1-процентном уровне значимости. Доверительные интервалы (уровни доверия) при этом будут равны 
и 
. Соответственно говорят о 95-процентном или о 99-процентном уровне доверия (надежности). Подчеркнем, что чем меньше уровень значимости (больше уровень доверия), тем шире соответствующий доверительный интервал (при прочих равных условиях).
Для расчета доверительных интервалов для параметров a и b уравнения линейной регрессии определяем предельную ошибку Δ для каждого показателя:
(8)
Величина tтабл представляет собой табличное значение t- критерия Стьюдента под влиянием случайных факторов при степени свободы k = n – 2 и заданном уровне значимости a.
|
|
|
Формулы для расчета доверительных интервалов имеют следующий вид:
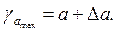
(9)
Если в границы доверительного интервала попадает ноль, т. е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Задача
Рассчитаем доверительный интервал для коэффициентов а и b,значения которых найдены в Лабораторной работе№1.
Решение.
1. Определите предельную ошибку для каждого показателя по формуле 8.
2. Определите доверительные интервалы для коэффициентов a, b по формуле 9 и запишите полученные границы доверительных интервалов.
Лабораторная работа №6.
Точечный и интервальный прогноз по уравнению линейной регрессии
Точечный прогноз заключается в получении прогнозного значения 
, которое определяется путем подстановки в уравнение регрессии: 
соответствующего (прогнозного) значения 
: 
.
Интервальный прогноз заключается в построении доверительного интервала прогноза, т. е. нижней и верхней границ уpmin, уpmax интервала, содержащего точную величину для прогнозного значения ŷp (уpmin< ŷp< уpmax). Доверительный интервал всегда определяется с заданной вероятностью (степенью уверенности), соответствующей принятому значению уровня значимости a.
Предварительно вычисляется стандартная ошибка прогноза 
:
, (10)
где 
.
Затем строится доверительный интервал прогноза, т. е. определяются нижняя 
и верхняя 
границы интервала прогноза:
; 
.
где 
Задача
Выполним прогноз ожидаемых расходов на питание у при прогнозном значении доходов х, составляющем 107% от среднего уровня. Оценим точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Решение.
1. Рассчитайте прогнозное значение , а затем прогнозное значение .
|
|
|
2. Рассчитайте ошибку прогноза по формуле 10.
3. Постройте доверительный интервал прогноза, сделайте выводы о надежности прогноза.
|
|
|
