 |
Анализ модели краткосрочного страхования жизни
|
|
|
|
В страховой компании застраховано N1=900 человек в возрасте 45 лет и N2=550 человек в возрасте 55 лет сроком на один год. Компания выплачивает наследникам: 100000 руб., в случае смерти застрахованного от несчастного случая, и 25000 руб., в случае смерти от естественных причин в течение года. Компания не платит ничего, если человек проживет этот год. Предположим, что смертность описывается моделью Мейкхама и рассчитаем нетто-премию, цену полиса, страховую надбавку, чтобы вероятность неразорения компании составляла 0,95.
Индивидуальные иски x  и x
и x  каждого из застрахованных 1-ой и 2-ой групп определяются, соответственно, рядами распределения (для удобства за денежную единицу примем 100000 руб.).
каждого из застрахованных 1-ой и 2-ой групп определяются, соответственно, рядами распределения (для удобства за денежную единицу примем 100000 руб.).
 |  |
0 ¼ 1 (1)
 x
x 
 =0,9982
=0,9982  =0,0013
=0,0013 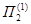 =0,0005
=0,0005


 0 ¼ 1
0 ¼ 1
 x
x 
 =0,9962
=0,9962 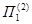 =0,0044
=0,0044  =0,0005
=0,0005
Здесь вероятности смерти от несчастного случая примем равными 0,0005, а вероятности смерти от естественных причин возьмем из Таблицы продолжительности жизни.
Средние индивидуальные иски Мx  и Мx
и Мx  равны соответствующим нетто-премиям Р
равны соответствующим нетто-премиям Р  и Р
и Р  для клиентов компании 1-ой и 2-ой групп.
для клиентов компании 1-ой и 2-ой групп.
Р 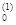 = Мx
= Мx  = ј*0,0013 + 1*0,0005» 0,00083 = 83 руб. (2)
= ј*0,0013 + 1*0,0005» 0,00083 = 83 руб. (2)
Р  = Мx
= Мx  = ј*0,0044 + 1*0,0005» 0,0016 = 160 руб.
= ј*0,0044 + 1*0,0005» 0,0016 = 160 руб.
I. Сначала рассмотрим решение, основанное на распределении Пуассона.
Чтобы свести задачу к схеме опытов Бернулли можно приближенно заменить ряды распределения (1) следующими таблицами:



 0 М(x
0 М(x  /x
/x  №0) 0 М(x
№0) 0 М(x  /x
/x  №0)
№0)

 x
x  : x
: x  : (3)
: (3)
|
|
|




а затем в качестве условной денежной единицы принять условные математические ожидания М(x 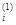 /x
/x  №0) в 1-ой таблице и М(x
№0) в 1-ой таблице и М(x  /x
/x  №0) – во 2-ой.
№0) – во 2-ой.
Вычислим условные математические ожидания:
М(x  /x
/x  №0)=ј*Р(x
№0)=ј*Р(x  =ј/x
=ј/x  №0)+1*Р(x
№0)+1*Р(x  =1/x
=1/x  №0) = =ј*
№0) = =ј*  /(
/( )+1*
)+1*  = =ј*0,0044/(0,0044+0,0005)+1*0,0005/(0,0044+0,0005)=
= =ј*0,0044/(0,0044+0,0005)+1*0,0005/(0,0044+0,0005)=
= ј*13/18+1*5/49 = 5/18 » 0,458=45800 руб. – денежная единица для клиентов 1-ой группы.
М(x  /x
/x  №0=ј*
№0=ј* 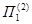 /(
/( )+1*
)+1*  =
=
=ј*0,0044/(0,0044+0,0005)+1*0,0005/(0,0044+0,0005) =
=. ј*44/49+1*5/49 = 16/49 » 0,327=32700 руб – денежная единица для клиентов 2-ой группы.
С учетом всех замечаний вместо рядов распределения (3) имеем:



 0 1 0 1
0 1 0 1

 x
x  : x
: x  : (4)
: (4)
0,9982 0,0018 0,9962 0,0049
откуда получаем: Мx  = 0,0018
= 0,0018
Мx  = 0,0049.
= 0,0049.
Подсчитаем сумму исков от застрахованных
1-ой группы:
l 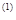 =
= 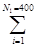 Мx
Мx  = N1* Мx
= N1* Мx  = 400*0,0018 = 0,7
= 400*0,0018 = 0,7
2-ой группы:
l 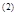 =
= 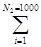 Мx
Мx  = N2* Мx
= N2* Мx  = 1000*0,0049 = 4,9
= 1000*0,0049 = 4,9
Общая сумма исков может рассматриваться, как случайная пуассоновская величина с параметром l  +l
+l  = 5,6
= 5,6
Так как вероятность не разорения компании должна быть не меньше 0,95, необходимо чтобы для общей суммы исков от застрахованных
x =  x
x  +
+  x
x 
выполнялось соотношение: Р(x Ј x) і 0,95, где х – капитал компании.
Очевидно, что х = х  , здесь х
, здесь х  » 10– квантиль уровня 0,95 для распределения Пуассона. За счет нетто-премий компания может получить только сумму:
» 10– квантиль уровня 0,95 для распределения Пуассона. За счет нетто-премий компания может получить только сумму:
5,6=0,7*45800 руб. + 4,9*32700 руб. = 32060 руб.+1060230 руб. = 192290руб.
Поэтому страховая надбавка компании должна составлять:
R=(10-5,6)/5,6 ×100%»78,6% = 0,786*192290 руб.»1511400руб., (5)
а капитал компании:
х = 192290 руб. + 151140 руб.» 343430 руб. (6)
Таким образом, индивидуальные страховые надбавки r 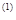 и r
и r 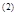 , цены полисов Р
, цены полисов Р 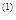 и Р
и Р 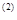 для каждого из клиентов 1-ой и 2-ой группы соответственно равны (они пропорциональны нетто-премиям):
для каждого из клиентов 1-ой и 2-ой группы соответственно равны (они пропорциональны нетто-премиям):
|
|
|
r 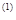 = 0,52*Р
= 0,52*Р 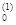 = 0,52*83 руб.» 43 руб.,
= 0,52*83 руб.» 43 руб.,
r 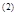 = 0,52*Р
= 0,52*Р  = 0,52*160 руб.» 83 руб.,
= 0,52*160 руб.» 83 руб.,
(7)
Р 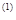 = Р
= Р 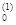 + r
+ r 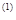 » 43 руб. + 83 руб. = 126 руб.,
» 43 руб. + 83 руб. = 126 руб.,
Р 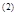 = Р
= Р  + r
+ r 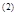 »160 руб. + 83 руб. = 243 руб.
»160 руб. + 83 руб. = 243 руб.
II. Теперь решим задачу с помощью гауссовского приближения. Среднее значение общего суммарного иска от застрахованных
x = 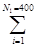 Мx
Мx  +
+  Мx
Мx 
с учетом средних индивидуальных исков (2) равно:
Мx = N1*Mx  + N2* Мx
+ N2* Мx  =400*0,00083+1000*0,0016=
=400*0,00083+1000*0,0016=
= 0,332 + 1,6» 1,9 = 190000 руб. (8)
Дисперсию x в виду независимости x  и x
и x  вычислим по формуле:
вычислим по формуле:
Dx = 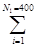 Dx
Dx  +
+  Dx
Dx  » 400*0,00058 + 1000*0,00078=
» 400*0,00058 + 1000*0,00078=
=0,23 + 0,78 = 1,01. (9)
Здесь:
Dx  = М(x
= М(x  )
)  - М
- М  x
x  = 0,00058 – (0,00083)
= 0,00058 – (0,00083)  » 0,00058,
» 0,00058,
(10)
Dx  = М(x
= М(x  )
)  - М
- М  x
x  = 0,00078 – (0,0016)
= 0,00078 – (0,0016)  » 0,00078,
» 0,00078,
где с помощью рядов распределения (1) имеем:
М(x  )
)  = 1/16*0,0013 + 1*0,0005» 0,00058,
= 1/16*0,0013 + 1*0,0005» 0,00058,
(11)
М(x  )
)  = 1/16*0,0044 +1*0,0005» 0,00078.
= 1/16*0,0044 +1*0,0005» 0,00078.
На основании центральной предельной теоремы функция распределения нормированной случайной величины:
 S
S  = (x - Mx)/
= (x - Mx)/  ,
,
при N1 + N2 ® Ґ имеет предел
F(x) = (1/  )*
)* 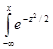 dz
dz
Для гауссовского приближения случайной величины x верна следующая цепочка равенств:
Р(x < x) = Р((x - Мx)/  Ј (х - Мx)/
Ј (х - Мx)/  )» F((x - Mx)/
)» F((x - Mx)/  ),
),
где х – капитал компании.
Для того чтобы вероятность неразорения компании не превосходила 0,95, т.е.
F((x - Mx)/  ) і 0,95 должно быть выполнено соотношение
) і 0,95 должно быть выполнено соотношение
(х - Mx)/  і х
і х  , (12)
, (12)
здесь х  » 1,645 – квантиль уровня 0,95 стандартного гауссовского распределения.
» 1,645 – квантиль уровня 0,95 стандартного гауссовского распределения.
Нетрудно убедиться в том, что минимально необходимый капитал компании должен составлять:
х=Мx+х  *
*  »1,9+1,645*1,005=1,9+1,65=3,55=355000руб., (13)
»1,9+1,645*1,005=1,9+1,65=3,55=355000руб., (13)
а относительная страховая надбавка составляет:
х  *
*  /Мx*100%=1,65/1,9*100%»86,8% (14)
/Мx*100%=1,65/1,9*100%»86,8% (14)
Индивидуальные страховые надбавки r  и r
и r 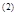 , цены полисов Р
, цены полисов Р  и Р
и Р 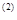 для клиентов 1-ой и 2-ой групп с учетом (2), очевидно будут равны (страховые надбавки пропорциональны нетто-премиям):
для клиентов 1-ой и 2-ой групп с учетом (2), очевидно будут равны (страховые надбавки пропорциональны нетто-премиям):
r  = 0,68*83 руб.» 56 руб.;
= 0,68*83 руб.» 56 руб.;
r 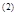 = 0,68*160 руб.» 109 руб.;
= 0,68*160 руб.» 109 руб.;
(15)
Р  = Р
= Р 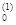 + r
+ r  »83 руб. + 56 руб. = 139 руб.;
»83 руб. + 56 руб. = 139 руб.;
Р 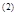 = Р
= Р  + r
+ r 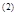 »160 руб. + 109 руб. = 269 руб.
»160 руб. + 109 руб. = 269 руб.
III. Проанализируем результаты, полученные в п.п. I и II. Очевидно расхождение результатов, полученных при использовании пуассоновского и гауссовского приближений. Попытаемся разобраться, в чем причина этого различия.
|
|
|
Дело в том, что при использовании закона Пуассона замена рядов распределения (1) на ряды распределения (3) привела к тому, что не изменились лишь математические ожидания Мx  и Мx
и Мx  . В то же время дисперсии Dx
. В то же время дисперсии Dx  и Dx
и Dx  , свидетельствующие о степени рассеяния случайных исков x
, свидетельствующие о степени рассеяния случайных исков x 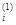 и x
и x  , найденных по рядам распределения (1) и (3), различны. Следовательно, различны и дисперсии Dx, найденные по рядам распределения (1) и (3). Действительно, дисперсия общего суммарного иска x по рядам (1) подсчитана: Dx = 1,24 (см. соотношение (9)).
, найденных по рядам распределения (1) и (3), различны. Следовательно, различны и дисперсии Dx, найденные по рядам распределения (1) и (3). Действительно, дисперсия общего суммарного иска x по рядам (1) подсчитана: Dx = 1,24 (см. соотношение (9)).
Вычислим дисперсию x по рядам распределения (3), т.е.



 0 0,458 0 0,327
0 0,458 0 0,327

 x
x  : x
: x  : (16)
: (16)
0,9982 0,0018 0,9962 0,0049
Проведя расчеты, аналогичные (9-11), получим:
Dx = 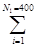 Dx
Dx  +
+ 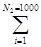 Dx
Dx  » 400*0,00038 + 1000*0,00052 = 0,67. (17)
» 400*0,00038 + 1000*0,00052 = 0,67. (17)
Здесь:
Dx  = М(x
= М(x  )
)  - М
- М  x
x  = 0,00038 – (0,00083)
= 0,00038 – (0,00083)  » 0,00038,
» 0,00038,
(18)
Dx  = М(x
= М(x  )
)  - М
- М  x
x  = 0,00052 – (0,0016)
= 0,00052 – (0,0016)  » 0,00052,
» 0,00052,
причем:
М(x  )
)  = 0,458
= 0,458  *0,0018» 0,00038,
*0,0018» 0,00038,
(19)
М(x  )
)  = 0,327
= 0,327  *0,0049» 0,00052.
*0,0049» 0,00052.
В дальнейшем будем использовать следующие обозначения: дисперсию x, найденную с использованием рядов (1), обозначим s 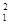 , а дисперсию x, найденную по рядам (3) или (16), обозначим s
, а дисперсию x, найденную по рядам (3) или (16), обозначим s 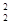 . Таким образом, s
. Таким образом, s 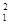 = 1,01, а s
= 1,01, а s 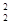 = 0,67.
= 0,67.
Из формулы (12), использующей стандартное гауссовское распределение, непосредственно следует, что относительная страховая надбавка, если Dx = s 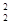 = 0,67, равна
= 0,67, равна
х  *s
*s 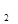 /Мx*100% = 1,645*
/Мx*100% = 1,645*  /1,9*100%» 70,9% (20)
/1,9*100%» 70,9% (20)
Этот результат хорошо согласуется с относительной страховой надбавкой, учитывающей распределение суммарного иска x по закону Пуассона, равной 86,8% (см. (5)).
Учитывая вышеизложенное, напрашивается естественный вывод: если относительная страховая надбавка, капиталл компании, обеспечивающий неразорение компании с вероятностью 0,95, и цена полиса вычисляются, исходя из распределения суммарного иска застрахованных по закону Пуассона, то для нахождения основных характеристик компании необходимо ввести поправочный коэффициент, равный k = s1 /s2.
|
|
|
Проиллюстрируем применение коэффициента k для коррекции результатов, полученных в п.I:
страховая надбавка с учетом (5) станет равной:
R 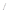 = k*R =
= k*R =  *86,8%=1,2*86,8%» 71,4%» 135660 руб. (21)
*86,8%=1,2*86,8%» 71,4%» 135660 руб. (21)
капитал компании (см.(6)) станет равным:
х 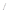 = 190000 руб. + 135660 руб.» 325660 руб., (22)
= 190000 руб. + 135660 руб.» 325660 руб., (22)
а индивидуальные страховые надбавки и цены полисов (см.(7)):
r 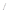
 = k*r
= k*r  » 1,2*43 руб.» 54 руб.,
» 1,2*43 руб.» 54 руб.,
r 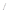
 = k*r
= k*r  » 1,2*83 руб.» 100 руб.,
» 1,2*83 руб.» 100 руб.,
(23)
Р 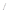
 = Р
= Р 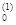 + r
+ r 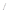
 » 83 руб. + 54 руб. = 137 руб.,
» 83 руб. + 54 руб. = 137 руб.,
Р 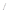
 = Р
= Р  + r
+ r 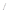
 » 160 руб. + 100 руб. = 260 руб.
» 160 руб. + 100 руб. = 260 руб.
В заключение необходимо отметить, что характеристики работы компании, полученные с учетом коррекции результатов исследования, в котором суммарный иск застрахованных подчинен распределению Пуассона хорошо согласуется с характеристиками работы страховой компании.
|
|
|


