Коэффициент автокорреляции

СТАТИСТИКА

КОНТРОЛЬНЫЕ РАБОТЫ

Для направления обучения

«Экономика»

Введение.. 2

Примеры решения задач.. 3

КОНТРОЛЬНЫЕ ЗАДАНИЯ.. 70

 

Введение

Целями освоения дисциплины «Статистика (теория статистики, социально-экономическая статистика)» является получение базовых знаний и формирование навыков при изучении технологического цикла получения статистических данных и их последующей обработки, системы статистических показателей и классификаций, а также рассмотрение наиболее важных направлений экономического анализа, основанного на данных экономической статистики.

Данное пособие поможет разобраться с основами методами расчетов, применяемыми во всех разделах статистики.

Таким образом, цель учебного пособия заключается в формировании у студентов системы знаний об особенностях статистических методов, их роли в экономической практике, преимуществах и возможностях статистического анализа.

Учебное пособие предназначено для студентов, обучающихся по направлению подготовки «Менеджмент».

В результате освоения дисциплины обучающийся должен:

знать:

- основные социально-значимые проблемы и процессы, происходящие в обществе (экономические, социальные), методы прогнозирования;

- основные показатели статистики;

- методики расчета экономических показателей;

уметь:

- анализировать основные закономерности экономических и социальных процессов на основе имеющихся фактических данных;

- делать прогноз на ближайшее будущее, применяя статистические методы;

владеть:

- методами обработки исходной информации,

- методами прогнозирования.

Примеры решения задач

Статистическая сводка и группировка материалов статистического наблюдения. Ряды распределения.

Пример 1.1. Имеются данные (таблица 1) о деятельности предприятия отрасли за 2007 г. На основе данных о числе цехов на каждом предприятии создать дискретный ряд распределения.

Таблица 1

Предприя-тия	Число цехов, ед.	Число рабочих, чел.	Объем производства, тыс. шт.	Затраты на производство, млн. руб.	Фонд заработной платы, тыс. руб.
				116,0	4608,0
				66,8	3026,4
				39,3	1950,0
				52,8	2622,0
				36,0	1612,0
				94,0	4914,0
				92,5	4456,7
				80,7	3430,0
				102,4	7005,8
				56,0	2982,0
				83,2	3947,9
				46,7	2754,0
				56,0	2520,0
				94,0	5130,0
				91,4	4329,0
				34,0	1364,0
				90,6	6000,0
				78,6	4080,0
				78,6	3887,4
				66,8	2882,5

Решение:

Проведем ранжирование первичного ряда, т.е. расположение всех вариант (числа цехов) в возрастающем порядке. Определяем частоты появления варианты (n_i) в данной совокупности. Далее находим накопленные частоты (n_xi). Находим частости (w_i =n_i/n) как отношение частоты к объему совокупности. И, наконец, суммированием частот всех предшествующих интервалов определяем накопленную частоту F_i. Результаты заносим в таблицу 2, которая отображает полученный дискретный ряд распределения.

Таблица 2

Число цехов (варианта), i	Количество предприятий с данным числом цехов (частота), ni	Накопленные частоты, nxi	Частости, wi	Накопленные относительные частоты, Fi
			0,2	0,2
			0,15	0,35
			0,15	0,5
			0,15	0,65
			0,2	0,85
			0,15
Σ

Пример 1.2. Используя данные о суммах затрат на производство из задачи 1 построить группировку предприятий с равными интервалами. Каждую группу охарактеризовать: количеством предприятий, числом цехов и числом рабочих всего.

Решение:

Выберем число интервалов группировки, используя формулу Стэрджеса:

k=1+3.32*lg(n)

n = 20, k=1+3.32*lg(20) ≈ 5

Находим ширину каждого из интервалов одинаковой ширины по следующей формуле:

Далее на основании первичной выборки распределяем варианты выборки по интервалам группировки, т.е. подсчитываем повторяемость вариант в каждом интервале. Для каждого интервала подсчитываем количеством предприятий, числом цехов и числом рабочих всего. Результаты заносим в таблицу 3.

Таблица 3

№ группы	Группы предприятий по суммам затрат на производство, млн. руб. (границы интервалов группы)	Количество предприятий в группе (ni)	Накопленные частоты (nxi)	Количество цехов в группе	Количество рабочих в группе
xi (ниж.)	xi (верх.)
		50,4
	50,4	66,8
	66,8	83,2
	83,2	99,6
	99,6
Σ

Задание 1.3. На основе исчисленных данных задач 1 и 2 построить:

– полигон распределения предприятий по числу цехов;

– гистограмму распределения предприятий по сумме затрат на производство;

– кумуляту распределения предприятий по числу цехов.

На графиках указать медиану и моду распределения и проверить значения аналитически.

Решение:

Mo

Me

i

Рис. 1. Полигон распределения предприятий по числу цехов.

Мода (Mo) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой.

Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.

Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины ∑|xi - Me|=min.

 

Определим ранг медианы для таблицы 2.

Медианой в данном случае может быть любое число между 3 и 4 членами ряда. Для определенности в данном случае в качестве медианы возьмем среднее арифметическое этих двух значений, т.е.

По определению мода в данном случае будет Mo = 3 – как признак, повторяющийся с наибольшей частотой.

 

Mo

Me

i

Рис. 2. Гистограмма распределения предприятий по сумме затрат на производство.

 

Определим модe и медианe по интервальному рядe для таблицы 3 на основе следующих формул:

где x₀ – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);

h – величина модального интервала;

n_Mo – частота модального интервала;

n_Mo-1 – частота интервала, предшествующего модальному;

n_Mo+1 – частота интервала, следующего за модальным.

В нашем случае x₀=83,2

 

где x₀ – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);

h– величина медианного интервала;

n_XMe-1 – накопленная частота интервала, предшествующего медианному;

n_Me – частота медианного интервала.

Нижняя граница медианного интервала x₀ = 66,8

 

Абсолютные и относительные величины

Пример 2.1. По предприятию за отчетный год имеются следующие данные о выпуске продукции:

Таблица 4

Наименование продукции	План на I квартал, тыс. шт.	Фактический выпуск, тыс. шт.	Отпускная цена за ед., руб.
январь	февраль	март

Определить процент выполнения квартального плана по выпуску каждого вида продукции и в целом по выпуску всей продукции.

Решение:

Для определения процента выполнения квартального плана рассчитаем показатель сравнения реально достигнутых результатов с намеченными ранее.

, где

Ф – достигнутый уровень в текущем периоде;

П – план на этот же период.

а) для продукции №1:

П₁ = 453; Ф₁ = 110+200+170 = 480 тыс. шт.

 

ОПВП₁ = Ф₁/П₁*100 = 480/453*100 = 105,9 %

 

б) для продукции №2:

П₂ = 125; Ф₂ = 80+115+96 = 291 тыс. шт.

 

ОПВП₂ = Ф₂/П₂*100 = 291/125*100 = 232,8 %

 

в) для всей продукции в целом:

Для расчета процента выполнения плана по выпуску всей продукции необходимо определить общий итог продукции по плану и фактический в денежном выражении:

SП₃ = k₁*П₁+ k₂*П₂ = 2200*453 + 2700*125 = 1334100 тыс. руб.;

SФ₃ = k₁*Ф₁+ k₂*Ф₂ = 2200*480 + 2700*291 = 1841700 тыс. руб.;

Тогда процент выполнения плана по выпуску всей продукции:

ОПВП₃ = SФ₃/SП₃*100 = 1841700/1334100 *100 = 138,05 %

Пример 2.2. В прошлом году объем товарооборота по торговому предприятию составил 367,0 млн. руб. Планом текущего было предусмотрено довести объем товарооборота до 550,0 млн. руб.; фактический объем товарооборота в текущем году составил 565,0 млн. руб.

Определить: относительную величину планового задания по росту товарооборота; относительную величину динамики товарооборота; относительную величину выполнения плана по товарообороту.

Решение:

а) Относительную величину планового задания вычисляем отношением уровня, запланированного на предстоящий период (П), к уровню показателя, достигнутому в предыдущем периоде (Ф₀):

 

Ф₀ =367,0 млн. руб; П = 550,0 млн. руб.;

Тогда = 149,8 %

б) Относительную величину динамики товарооборота вычисляем делением уровня признака за определенный период или момент времени на уровень этого же показателя в предыдущий период или момент времени:

ОПД = Ф₁ /Ф₀*100

 

Ф₀ =367,0 млн. руб; Ф₁= 565,0 млн. руб.;

Тогда ОПД = Ф₁ /Ф₀*100= 565.367*100= 153,95 %

 

в) Относительную величину выполнения плана по товарообороту (сравнения реально достигнутых результатов с намеченными ранее)вычисляем как отношение достигнутого уровня в текущем периоде к плану на этот же период:

Ф₁ – достигнутый уровень в текущем периоде; П – план на этот же период.

Ф₁ =565,0 млн. руб.; П = 550,0 млн. руб.;

= 102,72 %

Пример 2.3. Потребление электроэнергии в области характеризуется следующими данными: 2006 г. – 70,1 млрд. кВт∙ч; 2007 г. – 76,8 млрд. кВт∙ч. Численность населения области составила: на 1 января 2006 г. – 9,2 млн. чел.; на 1 января 2007 г. – 9,5 млн. чел.; на 1 января 2008 г. – 9,8 млн. чел.

Определить, на сколько процентов изменится потребление электроэнергии на душу населения.

Решение:

Потребление электроэнергии на душу населения определим по следующей формуле:

, где А - потребление электроэнергии за год,

N_ср – среднегодовая численность населения.

 

Запишем данные из условия задачи:

А₂₀₀₆ = 70,1 млрд. кВт∙ч; А₂₀₀₇ = 76,8 млрд. кВт∙ч;

Данные по численности на 1 января соответствующего года.

N₂₀₀₆ = 9,2 млн. чел.; N₂₀₀₇ = 9,5 млн. чел.; N₂₀₀₈ = 9,8 млн. чел.;

 

Получаем для 2006 г.:

 

для 2007 г.:

 

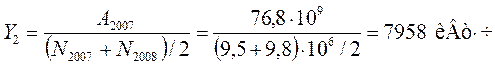
Тогда относительная величина динамики:

 

ОПД = Y₂/Y₁*100 = 7958/7497*100 = 106,15 %

 

Т.е. потребление электроэнергии на душу населения увеличится на 6,15 %.

Me

 

Рис. 3. Кумулята распределения предприятий по числу цехов.

 

Средние величины

Пример 3.1. По данным задачи (2.1) определить средний фактический выпуск продукции по фирме в целом.

Решение:

Определим средний фактический выпуск продукции по фирме в целом по формуле средней арифметической взвешенной:

 

, где w_i – вес (отпускная цена) i – ой продукции

Ф_i – фактический выпуск i – ой продукции

 

Возьмем данные из задания 2.1:

Ф₁ = 480 тыс. шт.; Ф₂ = 291 тыс. шт.; w₁ = 2200 руб.; w₂ = 2700 руб.;

 

Тогда

Пример 3.2. Используя данные задачи 1.1, определить: среднюю заработную плату одного рабочего; модальное и медианное значение затрат на производство.

Решение:

Внесем данные задачи 1.1. в таблицу 5 и рассчитаем среднюю заработную плату одного рабочего для каждого предприятия (группы):

, где - средняя заработная плата одного рабочего в группе (на предприятии), N – количество рабочих на предприятии

Теперь занесем данные в таблицу и рассчитаем среднюю групповую зарплату, т.е. среднюю заработную плату одного рабочего по всем предприятиям:

, где n – количество предприятий

Тогда

Таблица 5.

Предприятия	Число рабочих, чел.	Объем производства, тыс. шт.	Затраты на производство, млн. руб.	Фонд заработной платы, тыс. руб.	Средняя з/п на 1 рабочего
			116,0	4608,0	9,6
			66,8	3026,4	11,64
			39,3	1950,0
			52,8	2622,0	13,8
			36,0	1612,0	12,4
			94,0	4914,0	11,7
			92,5	4456,7	10,87
			80,7	3430,0	9,8
			102,4	7005,8	15,23
			56,0	2982,0	14,2
			83,2	3947,9	10,67
			46,7	2754,0	15,3
			56,0	2520,0
			94,0	5130,0	13,5
			91,4	4329,0	11,7
			34,0	1364,0	12,4
			90,6	6000,0
			78,6	4080,0
			78,6	3887,4	12,54
			66,8	2882,5	11,53
Σ					250,88

Модальное и медианное значение затрат на производство рассчитано в примере 1.1.

Пример 3.3. Известны данные о перевозке грузов по автотранспортному предприятию: январь – 35 тыс. т.; февраль – 37 тыс. т.; март – 42 тыс. т.; апрель – 45 тыс. т. Определить среднемесячный темп роста объема грузовых перевозок..

Решение:

Обозначим:

P₁ = 35 тыс. т.; P₂ = 37 тыс. т.; P₃ = 42 тыс. т.; P₄ = 45 тыс. т.;

Коэффициенты роста объема грузовых перевозок с переменной базой определяются следующим образом:

T_p1 = P₂/ P₁ = 37/35 = 1,057;

T_p2 = P₃/ P₂ = 42/37 = 1,135;

T_p1 = P₄/ P₃ = 45/42 = 1,071;

Тогда среднемесячный темп роста объема грузовых перевозок определится по формуле средней геометрической:

, т.е.

= 1,087 или 108,7 % (средний темп роста)

Пример 4.1. Распределение торговых фирм по размеру месячного товарооборота характеризуется следующими данными:

Таблица 6

Товарооборот, млн. руб.	До 5	5-10	10-15	15-20	20-25	25 и более	Итого
Число фирм

Определить средний размер месячного товарооборота на одну фирму.

Решение:

Для расчета будем использовать формулу средней арифметической взвешенной:

, где x’ – товарооборот; f – число фирм

Для каждого интервала предварительно вычислим среднее значение признака как полусумму нижнего и верхнего значений интервала. Величина открытых интервалов приравнивается к величине примыкающих к ним соседних интервалов:

Тогда

= (2,5*20+7,5*26+12,5*20+17,5*14+22,5*10+27,5*10)/2

12,4 млн. руб. - средний размер месячного товарооборота на одну фирму.

Пример 4.2. Определить за какой месяц и на сколько процентов была выше средняя месячная заработная плата работников предприятия, если известно:

Таблица 7

Цеха	Сентябрь	Октябрь
Численность работников	Средняя месячная заработная плата одного работника, руб.	Средняя месячная заработная плата одного работника, руб.	Фонд заработной платы, руб.

Решение:

 

Введем условные обозначения для сентября:

f – численность работников по каждому цеху;

x - средняя месячная заработная плата работников каждого цеха.

Определяющий показатель – общий фонд заработной платы Σ x f.

 

Средняя месячная заработная плата работников предприятия за сентябрь составила:

7024,77 руб.

 

Условные обозначения для октября следующие:

w – фонд заработной платы по каждому цеху;

x - средняя месячная заработная плата работников каждого цеха.

Определяющий показатель – общий фонд заработной платы Σ w.

Среднюю месячную заработную плату работников предприятия за октябрь вычисляем по формуле средней арифметической взвешенной:

 

6988,98 руб.

Динамика средней месячной заработной платы работников

0,9949 или 99,49 %

Следовательно, средняя месячная заработная плата работников предприятия в октябре понизилась на 0,51 % по сравнению с сентябрем.

Пример 4.3. При изучении покупательского спроса в обувных отделах торгового комплекса «Москва» получены следующие данные о распределении продаж мужской летней обуви по размерам:

Таблица 8

Размер								Итого
Число проданных пар

Проведите частотный анализ распределения и сделайте выводы. Для этого:

1) замените групповые частоты частостями;

2) для каждой группы определите кумулятивные частости;

3) постройте кумуляту распределения.

Решение:

Занесем данные (варианты и групповые частоты) задания в таблицу 9.

Далее находим частости (w_i =n_i/n) как отношение частоты к объему совокупности. И, наконец, суммированием частот всех предшествующих интервалов определяем кумулятивные частости F_i. Результаты также заносим в таблицу 9.

Таблица 9

Размер (варианта), i	Число проданных пар (частота), ni	Частости, wi	Кумулятивные частости, Fi
		0,07	0,07
		0,07	0,13
		0,13	0,27
		0,22	0,48
		0,32	0,80
		0,13	0,93
		0,07	1,00
Σ

Построим график распределения кумулятивных частостей (рис. 4.)

Рис. 4. График кумуляты распределения

Статистическое изучение вариации

Пример 5.1. По данным задачи (1.2) вычислить показатели вариации. Сделать выводы.

Решение:

Построим таблицу 1 и внесем туда часть данных из задания 1.2.

Рассчитаем середины интервалов x, произведение xf и внесем эти данные в таблицу 10.

Среднее значение определим по формуле средней арифметической взвешенной

Таблица 10

Группы предприятий по суммам затрат на производство, млн. руб. (границы интервалов группы)	Количество предприятий в группе (fi)	Середина интервала (х)	хf
xi (ниж.)	xi (верх.)
	50,4		42,2	168,80	-31,98	1022,72	4090,88
50,4	66,8		58,6	175,80	-15,58	242,74	728,21
66,8	83,2			375,00	0,82	0,67	3,36
83,2	99,6		91,4	548,40	17,22	296,53	1779,17
99,6			107,8	215,60	33,62	1130,30	2260,61
Σ							8862,232

Произведем расчет показателей вариации, используя данные таблицы 1:

1) Размах вариации = 116 – 34 =82 тыс. руб

2) дисперсия:

3) СКО:

4) КВ (коэффициент вариации):

Пример 5.2. Для установления зависимости между урожайностью и сортом винограда в одном из хозяйств на основе выборки определили урожай на 10 кустах винограда:

Таблица 11

Сорт	Число кустов	Урожай с одного куста, кг.
Изабелла					–	–
Мускат
Лидия				–	–	–

С помощью эмпирического корреляционного соотношения определить степень влияния признака, положенного в основу группировки на вариацию результативного показателя. Сформулировать выводы.

Решение:

Для решения задания составим новую таблицу 7.2, в которую внесем суммарные данные по объему урожая для каждого сорта.

Рассчитаем для каждой группы средние значения 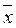, произведение и внесем эти данные в таблицу 12.

Групповое среднее значение определим по формуле средней арифметической взвешенной

Таблица 12

Сорт	Число кустов (f)	Урожай в целом, кг (xf)	Урожай в среднем на один куст, кг (x)
Изабелла				-0,9	0,81	2,43
Мускат				0,1	0,01	0,05
Лидия				1,1	1,21	2,42
Сумма						4,9
Среднее			6,9

Вычислим межгрупповую дисперсию по формуле:

 

Теперь вычислим общую дисперсию урожайности винограда на основе индивидуальных (несгруппированных) данных по формуле

Для этого создадим таблицу 13. и внесем туда данные из таблицы 11.

Таблица 13

Урожай с одного куста, кг. (y)	y2
Σ

 

тогда эмпирический коэффициент детерминации:

или 25,92%

Коэффициент детерминации говорит о том, что вариация урожайности винограда на 25,92% зависит от вариации сорта винограда и на 74,08% от прочих факторов.

 

Исходя из значений таблицы Чеддока можно заключить, что эмпирическое корреляционное отношение свидетельствует о заметной силе связи между сортом винограда и его урожайностью.

Пример 5.3. Имеются следующие данные о балансовой прибыли предприятий за два квартала:

Таблица 14

Квартал	Число предприятий	Балансовая прибыль, млн. руб.
I		18,4; 38,8; 72,6
II		14,1; 16,3; 48,8; 27,9

 

Определите:

1) среднюю из внутригрупповых, межгрупповую и общую дисперсию балансовой прибыли предприятия;

2) коэффициент детерминации и эмпирическое корреляционное отношение.

Сделайте выводы.

Решение:

1) Для решения задания составим новую таблицу 15, в которую внесем суммарные данные по объему урожая для каждого сорта.

Рассчитаем для каждой группы средние значения 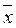, произведение и внесем эти данные в таблицу 15.

Групповое среднее значение определим по формуле средней арифметической взвешенной

Таблица 15

Квартал	Число предприятий(f)	Балансовая прибыль всего, (xf)	Балансовая прибыль в группе в среднем, млн. руб. (x)
I		129,80	43,27	9,42	88,81	266,42
II		107,10	26,78	-7,07	49,95	199,82
Сумма		236,90				466,24
Среднее			33,84

 

Вычислим внутригрупповую дисперсию внутри 1-ой и 2-ой группы:

, где - групповая средняя.

Для расчетов используем таблицу 16

 

 

Таблица 16

Квартал	Балансовая прибыль предприятия млн. руб. (x)	x2
I	18,4	338,56	-24,87	618,35
38,8	1505,44	-4,47	19,95
72,6	5270,76	29,33	860,44
Сумма				1498,75
Среднее	43,27
II	14,1	198,81	-12,68	160,66
16,3	265,69	-10,48	109,73
48,8	2381,44	22,03	485,10
27,9	778,41	1,13	1,27
Сумма				756,75
Среднее	26,78
Сумма всего		388,8195918

Тогда

= 499,58

= 189,19

Средняя из внутригрупповых дисперсий исчисляется как

,

где f – частота появления внутригрупповой дисперсии одной величины (одного размера).

= 322,21

Вычислим межгрупповую дисперсию, используя данные из таблицы 8.2. по формуле:

Теперь вычислим общую дисперсию балансовой прибыли на основе индивидуальных (несгруппированных) данных, используя данные таблицы 8.2 и 8.3 по формуле

=

Это же значение можно получить, используя формулу:

= 322,21 + 66,61 = 388,2

 

2)эмпирический коэффициент детерминации:

или 17,13%

Тогда эмпирическое корреляционное отношение

Коэффициент детерминации говорит о том, что вариация балансовой прибыли на 17,13% зависит от вариации квартала и на 82,87% от прочих факторов.

Исходя из значений таблицы Чеддока можно заключить, что эмпирическое корреляционное отношение свидетельствует об умеренной силе связи между номером квартала и балансовой прибылью предприятия.

 

Пример 5.4. Удельный вес основных рабочих в трех цехах предприятия составил: 70, 75, и 95% общей численности рабочих.

Определить дисперсию и среднее квадратическое отклонение доли основных рабочих по предприятию в целом, если численность всех рабочих трех цехов составило соответственно 150, 250 и 200 человек соответственно.

Решение:

Рабочие предприятия подразделяются на две группы: основные и ремонтно-вспомогательные рабочие.

Общая численность основных рабочих по предприятию в
целом составит:

 

Σn₀ = 0,7 • 150 + 0,75 • 250 + 0,95 • 200 = 482,5 ≈ 483 человека.

 

Доля основных рабочих по предприятию

 

р = Σn0 / Σn = 483/(150+250+200) = 0,805.

 

Дисперсия альтернативного признака

 

σ² = p*q

 

где р - доля единиц, обладающих данным признаком (доля основных рабочих);

q - доля единиц, не обладающих данным признаком (доля ремонтно-вспомогательных рабочих).

 

Поскольку р + q = 1, следовательно, q = 1 - р и формула дисперсии имеет вид:

 

σ² = p*(1-p) = 0,805*(1-0,805) = 0,157

 

Среднее квадратическое отклонение доли основных рабочих по предприятию в целом:

 

= 0,3962

Пример5.5. Распределение семей сотрудников финансовой корпорации по количеству детей характеризуется следующими данными:

Таблица 16

Количество детей в семье	Число семей сотрудников по подразделениям
1-е	2-е	3-е
			-

Определите:

1) внутригрупповые дисперсии;

2) среднюю из внутригрупповых дисперсий;

3) межгрупповую дисперсию;

4) общую дисперсию.

Проверьте правильность произведённых расчётов с помощью правила сложения дисперсий и рассчитайте эмпирическое корреляционное отношение.

Решение:

Для расчета общей дисперсии составим дискретный ряд распределения, промежуточные расчеты поместим в таблицу 17.

Таблица 17

Число семей, (x)	Количество повторов числа семей, (f)	xf
		1,00	-4,18	17,49	17,49
		2,00	-3,18	10,12	10,12
		9,00	-2,18	4,76	14,28
		4,00	-1,18	1,40	1,40
		5,00	-0,18	0,03	0,03
		6,00	0,82	0,67	0,67
		7,00	1,82	3,31	3,31
		10,00	4,82	23,21	23,21
		13,00	7,82	61,12	61,12
Сумма					131,64

Тогда групповое среднее значение определим по формуле средней арифметической взвешенной

57/11 = 5,18

Тогда общая дисперсия будет равна:

131,64/11 = 11,97

Величина этой дисперсии характеризует число семей с количеством детей от 0 до 3 под влиянием всех условий.

Различия в величине изучаемого признака прежде всего возникают под влиянием типа под

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: