Коэффициент автокорреляции

Линейный коэффициент автокорреляции r_t,t-1:

r_a=

 

Получается, что связь между рядами - высокая и прямая.

 

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=6 находим t_крит:

t_крит (n-m-1;α/2) = (6;0.025) = 2.447

где m = 1 - количество объясняющих переменных.

Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента автокорреляции. Другими словами, коэффициент автокорреляции статистически – значим.

 

Линейное уравнение регрессии имеет вид y = 0.18 x + 42.09

Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.

Для оценки качества параметров регрессии построим расчетную таблицу (табл. 38)

Таблица 38

x	y	y(x)	(yi-ycp)2	(y-y(x))2	(xi-xcp)2	|y - yx|:y
0.23	0.16	24.07	12946.65	571.57	10764.98	149.42
2.15	2.43	25.73	12435.22	542.92	10370.25	9.59
7.1	27.7	30.02	7437.91	5.38	9386.6	0.0837
25.03	70.8	45.55	1861.35	637.55	6233.8	0.36
100.31	119.9	110.76	35.48	83.53	13.5	0.0762
149.94	221.8	153.75	11633.06	4630.57	2111.91	0.31
200.1	187.3	197.2	5381.2	98.05	9238.2	0.0529
225.5	149.1	219.2	1235.99	4914.63	14766.03	0.47
225.5	246.3	219.2	17518.29	734.17	14766.03	0.11
935.86	1025.49	1025.49	70485.15	12218.38	77651.31	160.47

2) Выберем в качестве результативного и парного признаков столбцы «Прибыль – всего» и «Собственные средства с учетом резервов под риски», соответственно

Рассчитаем величину парного коэффициента корреляции по следующей формуле:

, где и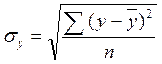

Для определения этих данных построим таблицу 24.4, внесем туда исходные данные, дополним ее необходимыми столбцами для расчета вышеуказанных значений.

Из данных табл. 24.4 видно, что:

.

Тогда

0,86

Таблица 39

Год	Прибыль – всего (y)	Собственные средства с учетом резервов под риски (x2)	y*x2	y2	x22	(y-yср)2	(x2-x2ср)2
	0,16	0,25	0,04	0,03	0,06	12946,65	163683,18
	2,43	3,50	8,51	5,90	12,25	12435,22	161063,99
	27,70	19,90	551,23	767,29	396,01	7437,91	148169,39
	70,80	88,10	6237,48	5012,64	7761,61	1861,35	100316,49
	119,90	246,10	29507,39	14376,01	60565,21	35,48	25194,51
	221,80	493,10	109369,58	49195,24	243147,61	11633,06	7791,99
	187,30	609,70	114196,81	35081,29	371734,09	5381,20	41972,63
	149,10	915,00	136426,50	22230,81	837225,00	1235,99	260275,70
	246,30	1267,80	312259,14	60663,69	1607316,84	17518,29	744721,06
Сумма	1025,49	3643,45	708556,68	187332,90	3128158,68	70485,15	1653188,92
Среднее	113,94	404,83	78728,52
σ	88,50	428,59
Rxy			0,86

 

Полученное значение коэффициента парной корреляции говорит в данном случае о наличии прямой (знак «плюс») и высокой (величина 0,86) связи между собственными средствами с учетом резервов под риски и прибылью всего.

Наличие автокорреляции устанавливается при помощи коэффи­циента автокорреляции для парной линейной связи.

Автокорреляцию для y определена в 1-ом пункте, определим автокорреляцию для x2:

Сдвигаем исходный ряд на 1 уровней. Получаем следующую таблицу:

 

yt	yt - 1
0.25	3.5
3.5	19.9
19.9	88.1
88.1	246.1
246.1	493.1
493.1	609.7
609.7
	1267.8

Параметры уравнения авторегрессии.

Выборочные средние.

 

Выборочные дисперсии:

 

 

Среднеквадратическое отклонение

 

 

Коэффициент автокорреляции

Линейный коэффициент автокорреляции r_t,t-1:

r_a=

Получается, что связь между рядами - весьма высокая и прямая.

 

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=6 находим t_крит:

t_крит (n-m-1;α/2) = (6;0.025) = 2.447

где m = 1 - количество объясняющих переменных.

Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента автокорреляции. Другими словами, коэффициент автокорреляции статистически – значим.

 

3) Выберем в качестве результативного и парного признаков столбцы «Прибыль – всего» и «Краткосрочные ссуды», соответственно

Рассчитаем величину парного коэффициента корреляции по следующей формуле:

, где и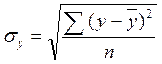

Для определения этих данных построим таблицу 40, внесем туда исходные данные, дополним ее необходимыми столбцами для расчета вышеуказанных значений.

Из данных табл. 40 видно, что:

.

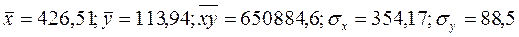Тогда

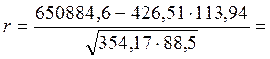0,76

Таблица 40

Год	Прибыль – всего (y)	Краткосрочные ссуды (x3)	y*x3	y2	x32	(y-yср)2	(x3-x3ср)2
	0,16	2,82	0,45	0,03	7,95	12946,65	179513,22
	2,43	13,77	33,46	5,90	189,61	12435,22	170354,31
	27,70	74,10	2052,57	767,29	5490,81	7437,91	124192,81
	70,80	191,80	13579,44	5012,64	36787,24	1861,35	55088,78
	119,90	802,10	96171,79	14376,01	643364,41	35,48	141067,85
	221,80	395,10	87633,18	49195,24	156104,01	11633,06	986,59
	187,30	597,80	111967,94	35081,29	357364,84	5381,20	29340,26
	149,10	970,30	144671,73	22230,81	941482,09	1235,99	295707,56
	246,30	790,80	194774,04	60663,69	625364,64	17518,29	132707,20
Сумма	1025,49	3838,59	650884,60	187332,90	2766155,61	70485,15	1128958,58
Среднее	113,94	426,51	72320,51
σ	88,50	354,17
Rxy			0,76

Полученное значение коэффициента парной корреляции говорит в данном случае о наличии прямой (знак «плюс») и высокой (величина 0,76) связи между краткосрочными ссудами и прибылью всего.

Наличие автокорреляции устанавливается при помощи коэффи­циента автокорреляции для парной линейной связи.

Автокорреляцию для y определена в 1-ом пункте, определим автокорреляцию для x3:

Сдвигаем исходный ряд на 1 уровней. Получаем следующую таблицу:

 

yt	yt - 1
2.82	13.77
13.77	74.1
74.1	191.8
191.8	802.1
802.1	395.1
395.1	597.8
597.8	970.3
970.3	790.8

 

Параметры уравнения авторегрессии.

Выборочные средние.

 

Выборочные дисперсии:

 

 

Среднеквадратическое отклонение

 

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: