Методические рекомендации к выполнению задания по методу корреляционно-регрессионного анализа (на примере анализа зависимости себестоимости 1ц зерновых культур от урожайности)

 

Исследование объективно существующих связей между явлениями – важнейшая задача статистики. Корреляционный метод предназначен для выявления и количественного определения тесноты связи между двумя признаками (при парной связи) и множеством признаков (при многофакторной связи).

Метод регрессионного анализа заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой результативным признаком) обусловлено влиянием одной или нескольких независимых величин (факторов).

Методика выполнения задания:

1. Представить данные себестоимости 1ц зерновых культур и урожайности зерновых на графике в виде диаграммы рассеивания. Сделать выводы о направлении, характере и тесноте связи.

 

 

,

 

Рис. 1- Зависимость себестоимости 1ц зерновых культур от урожайности.

 

На графике по оси 0 Х приводятся значения независимой переменной х; по оси 0 У – значения зависимой переменной y.

 

2. Рассчитать коэффициент парной линейной корреляции Пирсона.

коэффициент корреляции Пирсона определяем по формуле:

где σ_х – стандартное отклонение факторного признака x;

σ_у – стандартное отклонение результативного признака y.

где

Для выполнения расчетов составляется следующая таблица.

Таблица - Исходные и расчетные данные к определению коэффициента корреляции и параметров уравнения регрессии

№ района	Исходные данные	Вычисления
x	y	x2	y 2	xy
. n
Суммы	∑ x	∑ y	∑ x2	∑ y 2	∑ xy
Среднее

 

Интерпретация коэффициента корреляции между изучаемыми признаками дается в соответствии с принятой классификацией корреляционных связей:

Сильная, тесная при ≥0,7;

Средняя при 0,5≤ ≤0,69;

Умеренная при 0,3≤ ≤0,49;

Слабая при 0,2≤ r≤0,29;

Практически отсутствует ≤0,19.

Если r>0 – связь положительная;

Если r<0 – связь отрицательная.

 

3. Построить уравнение парной линейной регрессии, характеризующие связь между себестоимостью зерновых культур и урожайностью. Провести линию уравнения на графике.

Уравнение парной линейной регрессии имеет вид:

 

,

где а и b – параметры уравнения регрессии.

b – коэффициент регрессии показывает, на сколько в среднем происходит изменение результативной переменной y («+» – увеличение, «–» – снижение) при увеличении факторной переменной х на 1 единицу её измерения.

Для оценивания параметров а и b целесообразно использовать формулы, элементы которых рассчитаны выше.

,

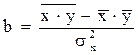где

, , - средние значения, - дисперсия признака х.

Приложение 5

Методические рекомендации к заданию по теме «Анализ временных рядов» (на примере статистического анализа динамики валового сбора зерновых культур в сельскохозяйственных организациях одного из регионов)

 

Одна из задач статистики заключается в изучении явлений и процессов в развитии, в динамике. Статистика должна дать характеристику изменений статистических показателей во времени. Для временных рядов свойственны две характеристики: тенденция изменения уровней ряда и колеблемость уровней относительно общей тенденции.

Анализ временных рядов охватывает решение задач построения, характеристики изменения социально-экономических явлений во времени, выявления основной тенденции, оценки устойчивости явления и тенденции. Тенденция и колеблемость дают основания для прогнозирования ожидаемых значений в будущем. В курсовой работе следует представить решение 7 задач, методика решения которых приведена ниже на примере временного ряда валового сбора зерновых культур.

 

Таблица 1 - Валовой сбор зерновых культур

Годы
валовой сбор, тыс. т.

 

1задача. Рассчитать абсолютные и относительные показатели изменения временного ряда, сравнивая каждый уровень ряда с предыдущим (цепные показатели) и с уровнем начального периода ряда (базисные показатели).

Исходные и рассчитанные показатели для наглядности представить в табличной форме (таблица 2).

Привести выводы по показателям последнего периода временного ряда.

 

таблица 2 - Показатели динамики валового сбора зерновых культур в сельскохозяйственных организациях региона

Годы	Уровни ряда, тыс. т. y	Абсолютное изменение, тыс. т.	Коэффициент роста	Темп роста, %	Темп прироста, %	Абсолютное значение 1 % прироста
Баз.	Цеп.	Баз.	Цеп.	Баз.	Цеп.	Баз.	Цеп.
		-	-	-	-	-	-	-	-	-

 

Столбец «Баз.» содержит так называемые базисные показатели динамики, которые рассчитываются путем сопоставления текущих уровней с уровнем первого года временного ряда, т. е. с уровнем 2007г.

Столбец «Цеп.» содержит так называемые цепные показатели динамики, которые рассчитываются путем сопоставления текущих уровней с уровнем предыдущего года временного ряда.

В приведенных ниже формулах i соответствует номеру периода временного ряда, i=1,2,…n.

Показатели динамики рассчитываются по формулам, приведенным ниже.

- Абсолютное изменение:

 

- Коэффициент роста:

 

- Темп роста:

 

 

- Темп прироста:

 

 

- Абсолютное значение 1 % прироста

 

 

2 задача. Рассчитать средние показатели динамики: средней уровень динамики, средний абсолютный прирост, средний коэффициент роста, средний темп роста, средний темп прироста. Сделать обобщающие выводы.

Расчеты выполнить по следующим формулам.

- Расчёт среднего уровня временного ряда выполняется по формуле среднего арифметического:

,

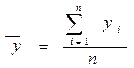где y_i – фактические уровни ряда динамики;

n – число периодов.

 

- Расчёт среднего абсолютного изменения уровней временного ряда проводится по формуле:

,

где y₁, y_n – уровни первого и последнего периода во временном ряду соответственно.

- Расчёт среднего коэффициента роста проводиться по формуле:

- Средний темп роста:

 

- Средний темп прироста:

 

 

3 задача. Описатьтенденцию динамики уровня временного ряда уравнением тренда. Подобрать вид математической функции тренда. Применяя метод наименьших квадратов, найти параметры уравнения тренда. Представить в виде графического изображения исходные уровни временного ряда, а также выровненные по уравнению тренда. Сделать выводы об общей тенденции динамики изучаемого процесса.

В данной задаче аналитическое выравнивание проводится по прямой, уравнение которой:

В этом уравнении приняты обозначения:

а,b – параметры;

t – условные обозначения периодов (моментов) времени;

– выровненные значения уровней временного ряда.

Способ наименьших квадратов даёт систему двух нормальных уравнений для нахождения параметров а и b:

 

 

Для проведения расчётов следует заполнить таблицу 3.

Таблица 3- Исходные и расчетные данные для определения параметров линейного тренда

Годы	Уровни ряда, тыс. тонн, y	t	t2	y ∙t	Выровненные уровни, тыс. тонн, ỹi
		-3
		-2
		-1
Итого:

 

Расчет параметров проводится по формулам:

Параметр b, коэффициент регрессии, показывает, на сколько в среднем увеличиваются (уменьшаются) уровни временного ряда ежегодно.

На графике по оси Х отмечаются периоды времени (годы), по оси Y значения фактических уровней y и строится прямая .

 

Рис.1- Динамика валового сбора зерновых культур

 

4 задача. оценить колеблемость валового сбора зерновых культур в течение исследуемого периода по годам на основе расчета показателей колеблемости: амплитуды колебаний, среднего линейного отклонения, среднего квадратического отклонения и коэффициентов колеблемости и устойчивости.

Исходные и расчетные данные для наглядности и систематизации вычислений представить в таблице.

 

Таблица 4 - Исходные и расчетные данные для определения показателей колеблемости, устойчивости и ошибки аппроксимации

 

Годы	yi	ỹi	ui = yi- ỹi	(yi-ỹi)2	Pt	Py	di2=(Pt-Py)2
Итого:

 

Расчеты показателей выполнить по формуле:

1. амплитуда колебаний:

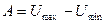
2. Среднее линейное отклонение:

,

где n – число исходных уровней;

p – число параметров уравнения тренда (для линейного тренда p = 2).

3. Среднее квадратическое отклонение:

4. Коэффициент колеблемости:

5. Коэффициент устойчивости:

K_уст. = 1-V_t

V_t, K_{уст .} – могут быть выражены в процентах.

 

5 задача. Установить устойчивость тенденции развития процесса, рассчитав ранговый коэффициент корреляции Спирмена.

Вспомогательные операции и расчеты выполнить в таблице 3.

P_t – ранги лет, обозначаются последовательно от 1 до n;

P_y - ранги уровней, обозначаются в соответствии с возрастанием уровней временного ряда от y _min, которому присваивается ранг равный 1, до y_max которому присваивается ранг n.

Формула рангового коэффициента корреляции Спирмена:

6 задача. Уравнение тренда проверить на адекватность, рассчитав среднюю ошибку аппроксимации.

Вспомогательные расчеты по определению ошибки аппроксимации выполнить в таблице 4 по формуле:

Средняя ошибка аппроксимации определяется по формуле среднего арифметического:

 

Считается, что если средняя ошибка аппроксимации не превышает 10%, уравнение тренда является адекватным, т.е. хорошо отражает тенденцию динамики.

7 задача. Составить прогноз относительно валового сбора зерновых культур на срок – 1-2 года (2014,2015 гг.) на основе тренда и колеблемости.

Методика статистического прогноза по тренду и колеблемости основана на их экстраполяции, т.е. на предположении, что параметры тренда и колебаний сохраняются до прогнозируемого периода.

1. Вычисляется «точечный прогноз». Для этого в уравнение тренда в качестве независимой переменной подставляют номер года прогноза t_k в соответствии с условными обозначениями фактора времени t в таблице 3 (для 2014года t_k = 4).

2. Статистические прогнозы имеют вероятностный характер. Поэтому строятся доверительные интервалы прогнозов, например с вероятностью 0,95. Для вычисления границ интервала рассчитывают среднюю ошибку прогноза положения линейного тренда на период прогноза t_k.

,

где S_t – среднее квадратическое отклонение.

Средняя ошибка прогноза умножается на величину t – критерия Стьюдента при указанной вероятности (0,95) и при числе степеней свободы n-2 (т.е. 5).

Для определения границ доверительного интервала применяется формула:

 

t – критерий Стьюдента берется из таблицы «Значение t – критерия Стьюдента при уровне значимости 0,05».

Содержательная интерпретация доверительного интервала прогноза: с вероятностью 0,95 можно утверждать, что прогнозируемый уровень временного ряда на период прогноза будет находиться в границах доверительного интервала.

Приложение 6

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: