Размерность физических величин.

 

Размерностью физических величин называется соотношение, на основании которого можно судить об изменении единицы сложной величины вследствие изменения основных единиц.

Так для ускорения 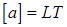  ^-2    

 

Это значит, что при увеличении единицы пути в n раз, в n раз увеличится и ускорение. При увеличении в m раз единицы времени, единица ускорения уменьшится в m² раз.

Формулы размерностей единиц сложных величин устанавливают закономерности, связывающие физические величины.

Обозначим размерности так:

[F]- размерность силы; [ v ] - размерность скорости; [а] -размерность ускорения и т.д.

 

L=[l] - размерность длины; [m]=M - размерность массы;

[t]=T - размерность времени.

Размерность любой физической величины в механике можно записать

L M T

 

где , ,  - любые целые, дробные, + и - числа, в частности они могут быть равны 0.

Т.к. физические законы не зависят от выбора единиц измерения, входящих в них физических величин, то размерности обеих частей уравнений этих законов должны быть одинаковыми.

Это правило используется для проверки правильности полученного результата, а также для установления размерностей физических величин.

Например, 1) установим размерность силы [F] в СИ

F=ma,             [F]=[m][a],              [m]=кг=М,

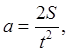
[t]=1c=T, [a]=LT^-2, 

 

[F]=MLT^-2 –формула размерности.

 

2) При решении задачи по определению силы получено выражение

W - энергия; t - время; v - скорость.

 

Известно, что сила в СИ измеряется в Ньютонах. Подставив в это выражение размерности входящих величин, мы можем убедиться в правильности полученного результата:

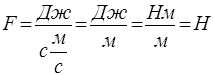
Иногда размерности частей уравнений не совпадают, тогда для устранения этого недостатка в правую часть выражения добавляют коэффициент пропорциональности. Значения К определяют опытным путем, а их размерности получают из основных законов.

Р

Например. Закон всемирного тяготения утверждает, что

но размерность [F] = LMT^{- 2} , не соответствует размерности из этой формулы [F]=L^-2M². Для устранения недостатка введен коэффициент пропорциональности – гравитационная постоянная, численное значение которой определено экспериментально (в СИ = 6,67х10^-11 м/кг*с²), а размерность из закона тяготения:     [ ]=L³M^-1T^-2,

       

 

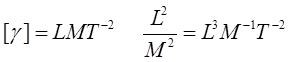
Таким образом:

 

Кинематика.

2.1. Системы отсчета и описание движения.

 

Механическое движение - процесс изменения положения тела или его частей по отношению к другим телам или друг другу.

Для описания механического движения необходимо указать тело, относительно которого рассматривается движение.

Произвольно выбранное неподвижное тело, по отношению к которому рассматривается движение данного тела, называется телом отсчета.

Связанная с этим телом произвольная система координат, называется системой отсчета. Чаще всего используют декартову прямоугольную систему.

Положение точки однозначно определяется 3-мя координатами М (х, у, z).

 

x = f₁(t)

y = f₂(t)

z = f₃(t)

 

Эти уравнения являются уравнениями движения материальной точки. Совокупность последовательных положений точки М в процессе ее движения, называется траекторией движения точки.

Для определения уравнения траектории необходимо исключить из уравнения время.

С точки зрения кинематики никакого различия между разными системами отсчета нет, они все совершенно равноценны.

Лекция 2.

Величины, характеризующие движение.

Поступательное движение.

Простейшим видом механического движения абсолютно твердого тела является поступательное движение - такое движение, при котором тело перемещается параллельно самому себе. При этом все точки описывают конгруэнтные (одинаковые) траекторий, смещенные друг относительно друга.

Поступательное движение абсолютно твердого тела может быть охарактеризовано движением какой-либо одной его точки, например, центра масс.

Для характеристики поступательного движения тела (материальной точка) вводится понятие перемещения.

 

Перемещением называется вектор, соединяющий начальное положение тела с его конечным положением.

Если положение точки в декартовой системе координат задано радиус-вектором, то перемещение можно определить как разность радиус векторов, характеризующих конечное (2) и начальное (1) положения точки, движущейся в течение промежутка времени Dt = t₂ - t₁    Dr = r₂ - r₁

Проекции вектора перемещения на координатные оси 0Х, 0У, 0Z

Dz_x = x₂ – x₁ = Dx

Dz_y = y₂ – y₁ = Dy

Dz_z = z₂ – z₁ = Dz

 

Dx, Dy, Dz – перемещение точки вдоль соответствующих осей.

В общем случае перемещение не совпадает с траекторией движения. Достаточно малое перемещение, которое с определенной степенью точ­ности можно считать совпадающим с соответствующим участком траектории, называется элементарным перемещением DS. Расстояние, пройденное телом при его движении по траектории, равно пути S. Путь - величина скалярная. В частных случаях перемещение и путь могут совпадать.

Мгновенная линейная скорость - физическая величина» равная пределу, к которому стремится отношение элементарного перемещения DS за промежутку времени Dt в течение которого совершается это перемещение, при Dt 0.

                  

Мгновенная скорость - векторная величина, имеющая тоже направление, что и касательная к траектории, т.к. вектор мгновенной скорости v совпадает с вектором достаточно малого перемещения dS за достаточно малое время dt. Мгновенная скорость численно равна первой производной от перемещения по времени.

Средняя скорость за промежуток времени Dt = t₂ - t₁ – это физическая величина, равная отношению вектора перемещения Dz к длительности промежутка времени Dt.

Средняя скалярная (путевая) скорость - физическая величина, определяемая отношением пути S, пройденного точкой за промежуток времени Dt к длительности этого промежутка:

   

Т.к. 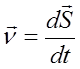 ,                       то ,     

,                ,                

Величину пройденного точкой пути можно представить графически пло­щадью фигуры ограниченной кривой  v = f (t) прямыми t = t₁ и t = t₁ и осью времени на графике скорости.

При движении точки мгновенная скорость может меняться как по величине, так и по направлению. При этом вектор   стремится к некоторому пределу, называемому линейным ускорением:

 

Т.о., ускорение - векторная величина, характеризующая изменение скорости в единицу времени, численно равная первой производной от мгновенной

скорости по времени или второй производной от перемещения по времени.

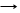В общем случае ускорение не совпадает по направлению с вектором скорости. Вектор ускорения а может быть представлен в виде 2-х взаимно перпендикулярных векторов: а_n – нормального ускорения, а  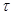– тангенциального ускорения. а  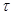 направлена вдоль касательной к траектории движения.

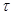 Полное ускорение а = а_n + а   Численное значение полного ускорения

За малый промежуток времени dt тангенциальное ускорение изменяет скорость на величину .

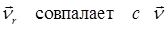, следовательно, тангенциальное ускорение изменяет только величину скорости

Нормальное ускорение а_n изменяет только направление скорости, численное значение а_{n  ,}

где - единичный вектор нормали к траектории движения.

Полное ускорение точки численно можно определить так:

Отметим, что при поступательном движении твердого тела все его точки имеют одинаковые скорости и ускорения и описывают одинаковые траектории, смещенные относительно друг друга.

 

Классификация движений.

 

Для классификаций движений воспользуемся формулой для определения полного ускорения

   

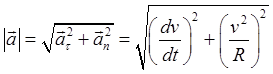
Предположим, что 

1)

Следовательно,  Это случай равномерного прямолинейного движения.

Но    

2)    Следовательно

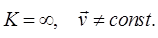
Это случай равномерного движения. В этом случае

При v₀ = 0 v_t = at – скорость равноускоренного движения без начальной скорости.

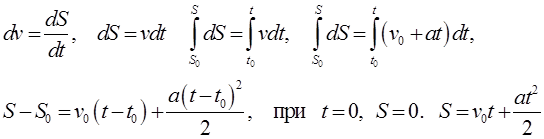
4)

Криволинейное движение с постоянной скоростью.

 

 

Лекция 3.

123	Поделиться:

Воспользуйтесь поиском по сайту: