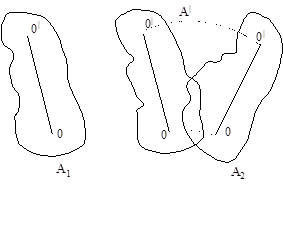Связь между линейной и угловой скоростью и ускорением.

Отдельные точки вращающегося тела имеют различные линейные скорости v, которые непрерывно изменяют свое направление и зависят от ω и расстояния r соответствующей точке до оси вращения.

Точка, находящаяся на расстоянии r от оси вращения проходит путь Δ S = r Δφ.

 

 

Поделим обе части равенства на Δ t:

, при Δ t 0 получим пределы от левой и правой частей равенства:

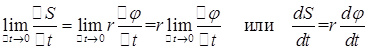
Но

Таким образом, чем дальше отстоит точка от оси вращения, тем больше ее линейная скорость. Известно, что

Откуда

Из написанных формул видно, что a _τ, a _n и a растут с увеличением расстояния точек до оси вращения. Формула v = ω r устанавливает связь между модулями векторов v, r, и ω, которые перпендикулярны друг к другу.

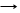
Т.к. ω | r, то можно написать v = ω∙ r ∙ sina это ничто иное как модуль векторного произведения. Таким образом

v = [ ω r ]  

 

Рассмотренные простейшие виды движения твердого тела важны потому,

 что любое движение твердого тела сводится к ним.

Рассмотрим два последовательных положения тела А₁ и А₂. Из положения А₁ в положение А₂ тело можно перевести следующим образом: вначале А₁ в А¹ поступательно. Затем из положения А¹ в положение А₂ путем поворота на угол φ вокруг произвольной точки 0.

Следует отметить, что в вращательному движению применимы все формулы кинематики материальной точки с заменой в них линейных величин на соответствующие угловые.

Например:

 

Колебательное движение.

Колебаниями или колебательными движениями являются движения или изменения состояния, обладающие той или иной степенью повторяемости во времени. Колебания весьма разнообразны по своей природе: колеба­ния пружинного маятника, качания маятников, колебания струн, вибра­ции фундаментов, качка корабля, колебания ветвей деревьев и т.д.

Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени: положение маятника в часах, Т – период, v = 1/T.

При изучении кинематики колебательных движений нас интересуют:

- закон, по которое повторяется движение;

- время, через которое тело (система) снова приходит к тому же самому состоянию;

- наибольшие отклонения, которых достигает движущееся тело и т.д.

Изучив эти характеристика колебательного движения, мы можем определить состояние тела (системы) в любой момент времени.

Все сложные виды колебательных движений можно свести к простейшим гармоническим колебаниям. Гармоническими колебаниями физической величины a называется процесс изменения ее во времени по закону sin или cos.

Например: колебания математического маятника, x = x₀cosωt колебания пружинного маятника.

Аналогично колебательного движения можно получить, если рассмотреть закон изменения проекции точки, движущейся по окружности на линию, лежащую в плоскости движения точки.

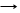Если радиус окружности r, угловая скорость вращения ω, то проекция

y = r sin φ = r sin ω t

если было начальное смещение на φ_0,

y = r sin ( ω t + φ₀ )

Аргумент синуса (или cos) наз. фазой. Фаза определяет положение колеблющейся величины в данный момент времени. φ₀ – начальная фаза, которая определяет положение точки в начальный момент времени t = 0

y = y₀ sin φ₀

ω - круговая или циклическая частота, т.е. число полных колебаний, которые совершаются за 2π единиц времени:

                                 ω = 2π v = 2π/Т

где v - частота колебаний, т.е. число полных колебаний за единицу времени;

Т - период колебания - наименьший промежуток времени, по истечении которого повторяются значения всех величин, характеризующих колебательное движение, т.е. время, за которое совершается полное колебание; у – смещение точки - удаление от положения равновесия в данный момент времени; у ₀ - амплитуда колебания - (наибольшее значение колеблющейся функции).

Вычислим скорость и ускорение точки, совершающей гармоническое колебание:

Знак " – " означает, что ускорение направлено в сторону, противоположную смещению. Изменение y, v, a с течением времени можно представить так:

t	y	v	a
0	0	ω y 0	0
T/4	y 0	0	– ω2 y 0
T/2	0	– ω y 0	0
3T/4	– y 0	0	ω2 y 0
T	0	ω y 0	0

 

Графически эти зависимости имеют вид:

 

Из таблицы и графика следует, что скорость имеет максимальные значения, когда точка проходит положения равновесия, а ускорение максимально в крайних положениях.

 

Сложение колебаний

Из теорий гармонического анализа известно, что любую периоди­ческую функцию f (x), имеющую период 2π, можно представить в виде тригонометрического ряда:

       

где a ₀, a_n, b_n  - коэффициенты этого ряда, определяемые по формулам:

Следовательно, любое сложное колебание можно предста­вить как сумму нескольких простых. Чтобы знать, как зависят парамет­ры сложного колебания от соотношения частот, амплитуд, фаз и направлений слагаемых колебаний, рассмотрим наиболее простые случаи сложения гармонических колебаний.

1. Сложение двух колебаний одного направления.

а) сложение 2-х колебаний одинаковой частоты.

ω₁ = ω₂ = ω, Т₁ = Т₂ = Т  Уравнения колебаний отличаются только начальной фазой и амплитудой и имеют вид:

                  

    Представим оба колебания в виде векторов амплитуды Х₀₁ и Х₀₂, Сложение векторов выполним графически.

Отложим от точки 0 под углом φ₁ – вектор Х₀₁, под углом φ₂ – вектор Х₀₂. Обе амплитуды вращаются с одинаковой угловой скоростью и против часовой стрелки. Следовательно, угол между амплитудами остается постоянным, равным (φ₂ – φ₁). Вектор Х₀ представляет собой гармоническое колебание, происходящее с той же частотой и амплитудой │Х₀│= │Х₀₁+ Х₀₂│ и начальной фазой φ. Из чертежа 

        

   

 

Само результирующее колебание имеет вид:

Важно заметить, что амплитуда результирующего колебания зависит от разности фаз (φ₂ – φ₁) слагаемых колебаний.

Она заключена в пределах:  

                   

1) Если разность начальных фаз слагаемых колебаний, равна четному числу π, φ₂ – φ₁ = к π, то Х₀ = Х₀₁ + Х₀₂, tg φ = tg φ₁, φ = φ₁, к = 0,1,2, …

Колебания однофазные и усиливают друг друга.

 

2) Если φ₂ – φ₁ = (2 к+ 1)π, то Х₀ = Х₀₁ - Х₀₂, к = 0,1,2,… следовательно колебания ослабляют друг друга  

 

 

3) Если Х₀₁ = Х₀₂ , ω₁ = ω₂ = ω, φ₂ = φ₁

 

 

Уравнение результирующего колебания имеет вид:

 

 – начальная фаза результирующего колебания.

Результирующее колебание гармоническое, отличающееся по фазе от слагаемых колебаний на половину суммы их начальных фаз.

 

При φ₁ – φ₂ = 2 к π, (к = 0,1,2,…) Х₀ = 2Х₀₁ – колебания усиливаются.

 

 

 

 

При φ₁ – φ₂ = (2 к + 1)π, (к = 0,1,2,…) Х₀ = 0 – колебания гасятся.

 

Биения.

Особый интерес представляет сложение колебаний одинакового направления с одинаковыми амплитудами, имеющими (близкие) мало отличающиеся частоты.

 

Результирующее суммарное колебание имеет уравнение:

 

Полученное выражение представляет собой произведение 2-х гармонических сомножителей с частотами    и .

Если ω₁ мало отличается от ω₂ , то частота  имеет близкие значения к ω₁ и ω₂ , а частота   – будет очень мала, т.е.

Отсюда следует, что результирующее колебание можно рассматривать как гармоническое колебательное движение, происходящее с круговой частотой  , периодом        и амплитудой

Причем амплитуда не остается постоянной, а медленно изменяется со временем. Частота изменения амплитуды   ,

а период амплитуды

 

 

Такие колебания называются биениями. Биения - такие колебания, амплитуда которых периодически возрастает и убывает по закону cos. Максимальная амплитуда наблюдается, если фазы слагаемых колебаний совпадают. Ясли эти колебания находятся в противофазе, то они гасят друг друга.

Биения часто встречаются при сложении колебаний и широко используются в радиотехнике.

 

3. Сложение взаимно перпендикулярных колебаний.

1) Рассмотрим движение точки М₁, участвующей одновременно в 2-х взаимно перпендикулярных колебаниях, частоты которых ω₁ и ω₂ равны (ω₁ = ω₂ = ω), амплитуды соответственно а и в.

Колебательный процесс в этом случае описывается системой уравнений:

где  φ – угол сдвига фаз.

Для определения уравнения траектории движения точки из системы уравнений исключим время. Из первого уравнения

Второе уравнение перепишем в виде:

Подставив вместо sin ωt и cos ωt их значения будем иметь уравнение движения 

Исследуем некоторые частные случаи.

а) при равенстве частот имеет место еще и равенство фаз, т.е. φ = 0.

Уравнение траектории имеет вид

Уравнение прямой, проходящей через начало координат под углом ά:

Смещение от начала координат определяется уравнением

 

 

Т.к. уравнение слагаемых колебаний имеет вид

 

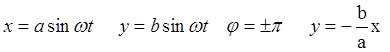
Таким образом результирующее движение является гармоническим колебанием.

б) составляющая колебания отличается по фазе на π/2. Уравнение траектории имеет вид:

отсюда    

- эллипс с плоскостями a и b.

 

 

При равенстве амплитуд траектории представляют собой окружность.

 

 

2) При сложении взаимно перпендикулярных колебаний, частоты которых кратны между собой, например ω₁ : ω₂ = 1/2, 2/3 и т.д. = m / n,

где m и  n – целые числа, колеблющееся тело описывает сложные кривые (наз. Фигурами Лисажу), форма которых определяется отношением частот складываемых колебаний, их амплитудой и разностью фаз между ними

ω₁ : ω₂ = 2: 1                                             ω₁ : ω₂ = 3: 2

 

 

 

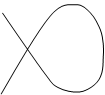Δφ = 0                Δφ = π / 2                                Δφ = 0                Δφ = π / 4

 

123	Поделиться:

Воспользуйтесь поиском по сайту: