 |
Принцип оптимальности в форме С-ядра
|
|
|
|
Кооперативные игры
Кооперативные игры получаются в тех случаях, когда, в игре n игроков разрешается образовывать определённые коалиции. Обозначим через N множество всех игроков, N ={1, 2,..., n }, а через S – любое его подмножество. Пусть игроки из S договариваются между собой о совместных действиях и, таким образом, образуют одну коалицию. Очевидно, что число таких коалиций, состоящих из r игроков, равно числу сочетаний из n по r, то есть 
, а число всевозможных коалиций равно
= 2 n – 1.
Из этой формулы видно, что число всевозможных коалиций значительно растёт в зависимости от числа всех игроков в данной игре. Для исследования этих игр необходимо учитывать все возможные коалиции, и поэтому трудности исследований возрастают с ростом n. Образовав коалицию, множество игроков S действует как один игрок против остальных игроков, и выигрыш этой коалиции зависит от применяемых стратегий каждым из n игроков.
Функция u, ставящая в соответствие каждой коалиции S наибольший, уверенно получаемый его выигрыш u(S), называется характеристической функцией игры. Так, например, для бескоалиционной игры n игроков u(S) может получиться, когда игроки из множества S оптимально действуют как один игрок против остальных N \ S игроков, образующих другую коалицию (второй игрок).
Характеристическая функция u называется простой, если она принимает только два значения: 0 и 1. Если характеристическая функция u простая, то коалиции S, для которых u(S)=1, называются выигрывающими, а коалиции S, для которых u(S) = 0, – проигрывающими.
Если в простой характеристической функции u выигрывающими являются те и только те коалиции, которые содержат фиксированную непустую коалицию R, то характеристическая функция u, обозначаемая в этом случае через u R, называется простейшей.
|
|
|
Содержательно простые характеристические функции возникают, например, в условиях голосования, когда коалиция является выигрывающей, если она собирает более половины голосов (простое большинство) или не менее двух третей голосов (квалифицированное большинство).
Более сложным является пример оценки результатов голосования в Совете безопасности ООН, где выигрывающими коалициями являются все коалиции, состоящие из всех пяти постоянных членов Совета плюс ещё хотя бы один непостоянный член, и только они.
Простейшая характеристическая функция появляется, когда в голосующем коллективе имеется некоторое “ядро”, голосующее с соблюдением правила “вето”, а голоса остальных участников оказываются несущественными.
Пусть коалиции как-то образованы. Тогда возникает вопрос: как делить общий выигрыш с учетом веса каждой коалиции между ее членами?
Принцип оптимальности в форме С-ядра
Естественно положить в основу анализа кооперативной игры принцип оптимального распределения максимального выигрыша u(S) между сторонами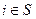 
.
Реализация этого принципа приводит к рассмотрению С-ядра − множество недоминируемых «вполне устойчивых» дележей кооперативной игры.
Вектор x = (x1,..., xn), удовлетворяющий условиям индивидуальной и коллективной рациональности, называется дележём в условиях характеристической функции u.
Распределение выигрышей (делёж) игроков должно удовлетворять следующим естественным условиям: если обозначить через xi выигрыш i- го игрока, то, во-первых, должно удовлетворяться условие индивидуальной рациональности
xi ³ u(i), для i ÎN (1)
т.е. любой игрок должен получить выигрыш в коалиции не меньше, чем он получил бы, не участвуя в ней (в противном случае он не будет участвовать в коалиции); во-вторых, должно удовлетворяться условие коллективной рациональности
|
|
|
= u(N) (2)
т.е. сумма выигрышей игроков должна соответствовать возможностям (если сумма выигрышей всех игроков меньше, чем u(N), то игрокам незачем вступать в коалицию; если же потребовать, чтобы сумма выигрышей была больше, чем u(N), то это значит, что игроки должны делить между собой сумму большую, чем у них есть).
Система { N, u}, состоящая из множества игроков, характеристической функции над этим множеством и множеством дележей, удовлетворяющих соотношениям (2) и (3) в условиях характеристической функции, называется классической кооперативной игрой.
Делёж x доминирует y, если существует такая коалиция S, для которой делёж x доминирует y. Это доминирование обозначается так: x > y.
Наличие доминирования x > y означает, что в множестве игроков N найдётся коалиция, для которой x предпочтительнее y. Соотношение доминирования возможно не для всякой коалиции. Так невозможно доминирование по коалиции, состоящей из одного игрока или из всех игроков.
Любой дележ из С-ядра устойчив, в том смысле, что ни одна из коалиций не имеет ни желания, ни возможности изменить исход игры.
Для того чтобы делёж x принадлежал с-ядру кооперативной игры с характеристической функцией u, необходимо и достаточно, чтобы для любой коалиции S выполнялось неравенство 
.
С-ядро может оказаться пустым, например, когда есть слишком сильные коалиции. Если С-ядро пусто, то требования всех коалиций одновременно не могут быть удовлетворены.
Пример. Найти С-ядро в кооперативной игре 3-х сторон, если максимальные гарантированные выигрыши всевозможных в данном случае семи коалиций (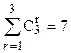
) следующие:
u(1, 2, 3)=9, u(2, 3)=7, u(1, 3)=4, u(1, 2)=4, u(1) =u(2) =u(3) =0.
Решение
Воспользуемся утверждением, раскрывающим метод построения С-ядра как множества недоминируемых дележей, т. е. для того, чтобы дележ x(S) принадлежал С-ядру необходимо и достаточно выполнения неравенств:
, S 
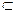N,
где xi − доля i -ой стороны;
i Î S, такая, что должно выполняться требование xi ³ u(i), i =1, 2, 3.
Составим соотношения (4 уравнения для 3 неизвестных):
x1+ x2 + x3≥9
x2 + x3≥7
x1 + x3≥4
x1+ x2 ≥4
x1≥0, x2 ≥0, x3≥0
Для нахождения x1, x2, x3 получаем следующие системы из 3-х неизвестных:
|
|
|
I. x1+ x2 + x3≥9 II. x1+ x2 + x3≥9
x2 + x3≥7 x2 + x3≥7
x1 + x3≥4 x1 + x2≥4
x1≥0, x2 ≥0, x3≥0 x1≥0, x2 ≥0, x3≥0
III. x1+ x2 + x3≥9 IV. x2 + x3≥7
x1 + x3≥4 x1 + x3≥4
x1 + x2≥4 x1 + x2≥4
x1≥0, x2 ≥0, x3≥0 x1≥0, x2 ≥0, x3≥0
Решением этих систем являются соответственно:
I − (x1=2, x2 = 5, x3 = 2); II − (x1=2, x2 = 2, x3 = 5);
III − (x1=0, x2 = 4, x3 = 5), (x1=0, x2 = 5, x3 = 4); IV − (x1=0.5, x2 = 3.5, x3 = 3.5).
Для кооперативных игр 3-х лиц, когда С-ядро не пусто, должно выполняться неравенство:
u(1, 2)+ u(1, 3)+u(2, 3) ≤ 2u(1, 2, 3) (3)
Таким образом, решение рассматриваемой игры (С-ядро) состоит из:
(x1=2, x2 = 5, x3 = 2), (x1=2, x2 = 2, x3 = 5), (x1=0, x2 = 4, x3 = 5), (x1=0, x2 = 5, x3 = 4),
а (x1=0.5, x2 = 3.5, x3 = 3.5) не удовлетворяет условию принадлежности С-ядру (3) − 0.5+3.5+3.5 = 7.5 < 9.
|
|
|
