 |
Принцип оптимальности в форме вектора Шепли
|
|
|
|
В случае, когда какая-то сторона (игрок) не является существенной, т. е. не принадлежит коалиции − носителю игры, то возникает необходимость конструирования принципа оптимальности как принципа справедливого дележа.
Одним из таких подходов является подход Шепли, суть которого в том, что он строиться на основании аксиом, отражающих справедливость дележей.
Носителем игры с характеристической функцией u называется такая коалиция T, что u(S) = u(S Ç T) для любой коалиции S.
Смысл носителя T состоит в том, что любой игрок, не принадлежащий T, является нейтральным, он не может ничего внести в коалицию и ему ничего не следует выделять из общих средств.
Пусть u – характеристическая функция кооперативной игры n игроков, p – любая перестановка множества N игроков. Через pu обозначим характеристическую функцию и такой игры, что для коалиции S = { i1, i2,..., iS } будет u ({p(i1), p(i2),..., p(iS)}) = u(S).
Содержательный смысл функции pu состоит в том, что если в игре с характеристической функцией u поменять местами игроков согласно перестановке p, то получим игру с характеристической функцией pu.
Аксиомы Шепли
1. Аксиома симметрии. Для любой перестановки p и iÎN должно выполняться 
(pu) = j i (u), т.е. игроки, одинаково входящие в игру, должны “по справедливости” получать одинаковые выигрыши.
2. Аксиома эффективности. Если S – любой носитель игры с характеристической функцией u, то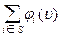 
= u(S)
Иными словами, “справедливость требует”, что при разделении общего выигрыша носителя игры ничего не выделять на долю посторонних, не принадлежащих этому носителю, равно как и ничего не взимать с них.
3. Аксиома агрегации. Если есть две игры с характеристическими функциями u¢ и u¢¢, то j i (u¢ + u¢¢) = j i (u¢) + j i (u¢¢),
|
|
|
т.е. ради “справедливости” необходимо считать, что при участии игроков в двух играх их выигрыши в отдельных играх должны складываться.
Вектором цен (вектором Шепли) игры с характеристической функцией u называется n-мерный вектор j (u) = (j1(u), j2(u),..., jn(u)), удовлетворяющий аксиомам Шепли.
j i (u) − компонента вектора j (u), представляющая полезность (выигрыш) i -го игрока в кооперативной игре в результате соглашения или решения арбитра.
Можно доказать, что компоненты вектора Шепли в явном виде запишутся следующим образом
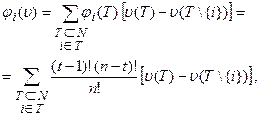(4)
где t – число элементов в T.
Вектор Шепли содержательно можно интерпретировать следующим образом: предельная величина, которую вносит i -й игрок в коалицию T, выражается как
u(T) - u(T \{ i }) и считается выигрышем i- го игрока;
j i (u) – средний выигрыш i -го игрока в такой схеме интерпретации.
В том случае, когда u – простейшая,
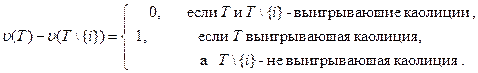
Следовательно
,
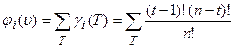где
g i (T) – это вероятность того, что i -й игрок вступит в коалицию T \{ i };
суммирование по T распространяется на все такие выигрывающие коалиции T, что коалиция T \{ i }не является выигрывающей.
Вектор Шепли удовлетворяет всем аксиомам Шепли и является заданием принципа оптимальности в кооперативной игре, когда С-ядро пусто или когда оно не пусто, но вектор Шепли ему не принадлежит.
Пример 1. Рассматривается корпорация из четырёх акционеров, имеющих акции соответственно в следующих размерах:
a1 = 10, a2 = 20, a3 = 30, a4 = 40.
Любое решение утверждается акционерами, имеющими в сумме большинство акций. Это решение считается выигрышем, равным 1. Поэтому данная ситуация может рассматриваться как простая игра четырёх игроков, в которой выигрывающими являются следующие коалиции:
{2; 4}, {3; 4},
{1; 2; 3}, {1; 2; 4}, {2; 3; 4}, {1; 3; 4},
{1; 2; 3; 4}.
Найти вектор Шепли для этой игры
Решение
При нахождении j1 необходимо учитывать, что имеется только одна коалиция T = {1; 2; 3}, которая выигрывает, а коалиция T \{1} = {2; 3} не выигрывает. В коалиции T имеется t = 3 игрока, поэтому
|
|
|
.
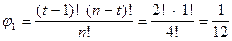Далее, определяем все выигрывающие коалиции, но не выигрывающие без 2-го игрока: {2; 4}, {1; 2; 3}, {1; 2; 4}. Поэтому
.
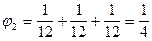Аналогично получаем, что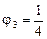 
, 
.
В результате получаем, что вектор Шепли равен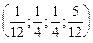 
. При этом, если считать, что вес голоса акционера пропорционален количеству имеющихся у него акций, то получим следующий вектор голосования
,
который, очевидно, отличается от вектора Шепли.
Анализ игры показывает, что компоненты 2-го и 3-го игроков равны, хотя третий игрок имеет больше акций. Это получается вследствие того, что возможности образования коалиций у 2-го и 3-го игрока одинаковые. Для 1-го и 4-го игрока ситуация естественная, отвечающая силе их капитала.
Пример 2. Пусть n различных потребителей должны построить хранилища спецпродукции, при нарушении правил хранения которой может возникнуть опасная ситуация. Затраты на строительство зависят от объема хранилищ. Потребности в продукции потребителей определяются функциями fi(t), i=1,2,…,n. Для постройки хранилищ потребители могут организовывать коалиции S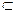 
N, N={1,2,…,n}. Затраты на создание хранилищ заданы такой возрастающей функцией, что характеристическая функция принимает значения:
| Коалиция | {1} | {2} | {3} | {1, 2} | {1, 3} | {2, 3} | {1, 2, 3} |
| u(S) | 2.5 | 3.9 |
Определить число хранилищ и коалиции, которые их будут строить. Члены коалиции равноправны.
Решение
Для вычисления распределения расходов между членами коалиции воспользуемся вектором Шепли (4).
1. Вклад 1-го потребителя, если создается коалиция S = {1,2,3} равен:
j 1(2, 3) (u) =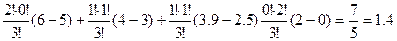 
,
где ↕ ↕ ↕ ↕
n = 3, t = 3 t = 2 t = 2 t = 1
6→{1, 2, 3}, 5→{2, 3}, 4→{1, 2}, 3→{2}, 3.9→{1, 3}, 2.5→ {3}, 2→{1}, 0→{0}
В ыигрыш u(S)=6 коалиции S = {1,2,3} и т. д.
Вклад 2-го потребителя, если создается коалиция S = {1,2,3} равен:
j 2(1, 3) (u) = 
,
где ↕ ↕ ↕ ↕
n = 3, t = 3 t = 2 t = 2 t = 1
6→{1, 2, 3}, 3.9→{1, 3}, 4→{1, 2}, 2→{1}, 5→{2, 3}, 2.5→ {3}, 3→{2}, 0→{0}
Вклад 3-го потребителя, если создается коалиция S = {1,2,3} равен:
j 3(1, 2 ) (u) = 
,
где ↕ ↕ ↕ ↕
n = 3, t = 3 t = 2 t = 2 t = 1
6→{1, 2, 3},4→{1,2}, 3.9→{1, 3}, 2→{1}, 5→{2, 3}, 3→ {2}, 2.5→{3}, 0→{0}
2. Вклад 1-го потребителя, если создается коалиция S = {1,2} равен:
|
|
|
j 1(2 ) (u) =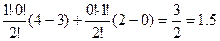 
,
где ↕ ↕
n = 2, t = 2 t = 1
4→{1, 2}, 3→{2}, 2→{1}, 0→{0}
Вклад 1-го потребителя, если создается коалиция S = {1,3} равен:
j 1(3 ) (u) = 
,
где ↕ ↕
n = 2, t = 2 t = 1
3.9→{1, 3}, 2.5→{3}, 2→{1}, 0→{0}
Вклад 2-го потребителя, если создается коалиция S = {2,1} равен:
j 2(1 ) (u) =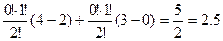 
,
где ↕ ↕
n = 2, t = 2 t = 1
4→{1, 2}, 2→{1}, 3→{2}, 0→{0}
Вклад 2-го потребителя, если создается коалиция S = {2,3} равен:
j 2(3 ) (u) =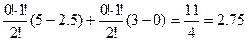 
,
где ↕ ↕
n = 2, t = 2 t = 1
5→{3, 2}, 2.5→{3}, 3→{2}, 0→{0}
Вклад 3-го потребителя, если создается коалиция S = {3,1} равен:
j 3(1 ) (u) =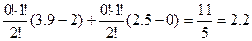 
,
где ↕ ↕
n = 2, t = 2 t = 1
3.9→{1, 3}, 2→{1}, 2.5→{3}, 0→{0}
Вклад 3-го потребителя, если создается коалиция S = {3,2} равен:
j 3(2 ) (u) =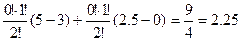 
,
где ↕ ↕
n = 2, t = 2 t = 1
5→{2, 3}, 3→{2}, 2.5→{3}, 0→{0}
3. Вклады потребителей, если они входят в коалиции S ={1}, S ={2}, S ={3} заданы в таблице и равны:
j 1(1 ) (u) = 2, j 2(2 ) (u) = 3, j 3(3 ) (u) = 2.5
Сравним вычисленные вклады для потребителей при вхождении их в различные коалиции.
Имеем:
j 1(1 ) (u) > j 1(2 ) (u) >j 1(2,3 ) (u) j 1(1 ) (u) > j 1(3 ) (u) >j 1(2,3 ) (u)
2 1.5 1.4 2 1.7 1.4
j 2(2 ) (u) > j 2(1 ) (u) >j 2(1,3 ) (u) j 2(2 ) (u) > j 2(3 ) (u) >j 2(1,3 ) (u)
3 2.5 2.45 3 2.75 2.45
j 3(3 ) (u) > j 3(1 ) (u) >j 3(1,2 ) (u) j 3(3 ) (u) > j 3(2 ) (u) >j 3(1,2 ) (u)
2.5 2.2 2.15 2.5 2.25 2.15
Так как вектор Шепли в данном примере характеризует затраты на создание хранилищ, то из сравнения вкладов видно, что потребителям выгоднее объединиться в коалицию S = {1,2,3} и строить одно хранилище.
Пример 3. Решить пример 2 (строительство хранилища спецпродукции) путем вычисления С-ядра.
Решение
Составим соотношения (4 уравнения для 3 неизвестных):
x1+ x2 + x3≥6
x2 + x3≥5
x1 + x3≥3.9
x1+ x2 ≥4
x1≥2, x2 ≥3, x3≥2.5
Для нахождения x1, x2, x3 получаем следующие системы из 3-х неизвестных:
I. x1+ x2 + x3≥6 II. x1+ x2 + x3≥6
x2 + x3≥5 x2 + x3≥5
x1 + x3≥3.9 x1 + x2≥4
x1≥2, x2 ≥3, x3≥2.5 x1≥2, x2 ≥3, x3≥2.5
III. x1+ x2 + x3≥6 IV. x2 + x3≥5
x1 + x3≥3.9 x1 + x3≥3.9
x1 + x2≥4 x1 + x2≥4
x1≥2, x2 ≥3, x3≥2.5 x1≥2, x2 ≥3, x3≥2.5
Решением этих систем являются соответственно:
I − (x1=1, x2 = 2.1, x3 = 2.9); II − (x1=1, x2 = 3, x3 = 2);
|
|
|
III − (x1=1.9, x2 = 2.1, x3 = 2); IV − (x1=1.45, x2 = 2.55, x3 = 2.45).
Видно, что эти значения в совокупности не удовлетворяют условиям:
x1≥2, x2 ≥3, x3≥2.5.
Отсюда делаем вывод, что С-ядро пустое и принцип оптимальности надо искать на основе вычисления вектора Шепли.
|
|
|
