 |
Задача оптимизации финансовых инвестиционных ресурсов.
|
|
|
|
Рассмотрим задачи оптимизации распределения средств между инвестиционными объектами на примерах.
Имеются три инвестора и четыре инвестиционных объекта. Инвестиционные мощности инвесторов и спрос на инвестиции, а также инвестиционные затраты для каждой пары «инвестор – инвестиционный объект» сведены в таблицу инвестиций (таблица 1).
Таблица 1
| Инвесторы | Мощности инвесторов | Инвестиционный спрос | |||
В левом верхнем углу произвольной (i,j) клетки стоит коэффициент инвестиционных затрат i–го инвестора для j-го объекта. Задача формулируется следующим образом: найти объемы инвестиций для каждой пары «инвестор – инвестиционный объект» так, чтобы: мощности всех инвесторов были реализованы, все инвестиционные спросы были удовлетворены, суммарные инвестиционные затраты были бы минимальны. Обозначим через xij объем инвестиций от i –го инвестора к j-му объекту. Заданные мощности инвесторов и инвестиционный спрос накладывают ограничения на значения неизвестных xij. Чтобы мощность каждого из инвесторов была реализована, необходимо составить уравнения баланса для каждой строки таблицы инвестиций:
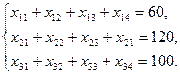
Аналогично, чтобы спрос каждого объекта был удовлетворен, подобные уравнения баланса составляются для каждого столбца таблицы инвестиций:
Очевидно, что объем инвестиций не может быть отрицательным, поэтому следует ввести ограничение не отрицательности переменных:
xij ≥0.
Суммарные затраты F на инвестиции выражаются через коэффициенты инвестиционных затрат следующим образом:
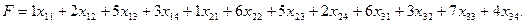
Для математической постановки задачи оптимизации распределения средств между инвестиционными объектами в общей постановке обозначим через сij коэффициенты затрат, через Mi – мощности инвесторов, через Nj – инвестиционный спрос, (i=1,2,…,m)., (j=1,2,…,n), m – число инвесторов, n – число инвестиционных объектов. Тогда система ограничений примет вид:
|
|
|
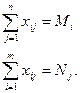(1)
Система (7) включает в себя уравнения баланса по строкам и по столбцам.
При этом суммарная мощность инвесторов равна суммарному инвестиционному спросу, т.е.
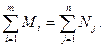
Целевая функция в данном случае следующая:
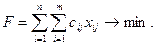(2)
Таким образом, на множестве неотрицательных решений системы ограничений (1) найти такое решение, при котором значение целевой функции (2) будет минимально.
На фондовой бирже брокеру необходимо определить акции, каких компаний необходимо приобрести инвесторам, чтобы прибыль от вложения была максимальной. Исходные данные для решения задачи сведены в таблицу 2.
Таблица 2
| Инвесторы | Мощности инвесторов | Инвестиционный спрос на акции | |||
В левом верхнем углу произвольной (i,j) клетки стоит коэффициент прибыли i –го инвестора для j-го пакета акций. Задача формулируется следующим образом: найти объемы вложений в акции для каждой пары «инвестор – пакет акций» так, чтобы: мощности всех инвесторов были реализованы, все инвестиционные спросы на акции были удовлетворены, суммарная инвестиционная прибыль была бы максимальной. Обозначим через xij объем вложений в акции от i –го инвестора в j-ый пакет акций. Заданные мощности инвесторов и инвестиционный спрос на акции накладывают ограничения на значения неизвестных xij.
В приведенной задаче инвестиционный спрос на акции превышает мощности инвесторов на 60 ед. Т.е. задача является открытой. Для решения открытой задачи необходимо ввести фиктивного инвестора (фиктивный инвестиционный спрос на акции, если мощности инвесторов превышают инвестиционный спрос на акции). Таким образом будет добавлена 5-я строка в табл. 2. Коэффициенты прибыли для пятой строки принимаются равными 0. Конкретное значение этого коэффициента не влияет на решение.
|
|
|
Чтобы мощность каждого из инвесторов была реализована, необходимо составить уравнения баланса для каждой строки таблицы инвестиций:
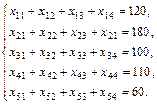
Аналогично, чтобы спрос на акции был удовлетворен, подобные уравнения баланса составляются для каждого столбца таблицы инвестиций:
Очевидно, что объем вложений в акции не может быть отрицательным, поэтому следует ввести ограничение не отрицательности переменных:
xij ≥0.
Суммарная прибыль F от вложений в акции выражается через коэффициенты прибыли на одну акцию следующим образом:
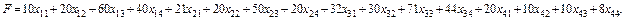
Рассмотри задачи оптимизации инвестиционных ресурсов.
Все направления и формы инвестиционной деятельности предприятия осуществляются за счет формируемых им инвестиционных ресурсов. От характера формирования этих ресурсов во многом зависит уровень эффективности инвестиционной деятельности предприятия. Инвестиционные ресурсы предприятия представляют собой все формы капитала, привлекаемого для осуществления вложений в объекты реального и финансового инвестирования.
Условия формирования высоких конечных результатов инвестиционной деятельности в значительной степени зависят от структуры сформированных инвестиционных ресурсов. Оптимальная структура инвестиционных ресурсов обеспечивает финансовое равновесие развития предприятия. Процесс формирования инвестиционных ресурсов предприятия должен формироваться с позиции минимизации затрат по формированию инвестиционных ресурсов в процессе инвестиционной деятельности или с позиции максимизации прибыли от вложения инвестиционных ресурсов. Современная инвестиционная теория выделяет следующие основные виды инвестиционных ресурсов:
1. Инвестиционные ресурсы в денежной форме.
2. Инвестиционные ресурсы в финансовой форме (акции, облигации, депозитные счета и сертификаты банков).
3. Инвестиционные ресурсы в материальной форме (машины, оборудование, здания, оборудования, сырье, материалы, полуфабрикаты).
|
|
|
4. Инвестиционные ресурсы в нематериальной форме (права пользования отдельными природными ресурсами, патентные права, «ноу-хау», права на товарные знаки, компьютерные программы).
Рассмотрим задачу оптимизации материальных инвестиционных ресурсов.
Для изготовления двух видов продукции P1 и P2 используют четыре вида ресурсов S1, S2, S3, S4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в табл. 3 (цифры условные).
Таблица 3
| Вид ресурса | Запас ресурса | Число единиц ресурсов, затрачиваемых на изготовление единицы продукции | |
| P1 | P2 | ||
| S1 | |||
| S2 | |||
| S3 | - | ||
| S4 | - |
Прибыль, получаемая от реализации единицы продукции P1 и P2 соответственно, составляет 2 и 3 грн.
Необходимо составить такой план производства продукции, при котором прибыль от реализации будет максимальной.
Составим оптимизационную модель задачи.
Обозначим x1, x2 – число единиц продукции соответственно P1 и P2, запланированных к производству. Для их изготовления (табл. 1) потребуется (1* x1+3* x2) единиц ресурса S1, (2* x1+1* x2) единиц ресурса S2, (1* x2) единиц ресурса S3, (3* x1) единиц ресурса S4. Так как потребление ресурсов S1, S2, S3, S4 не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выражается системой неравенств:
Переменные неотрицательные x1³0, x2³0.
Суммарная прибыль F от реализации продукции составит:
.
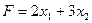В математической постановке задача формулируется следующим образом. Обозначим Xj (j=1,2,…,n) – число единиц продукции Pj, запланированных к производству; bi (i=1,2,…,m) – запас ресурса Si; aij – число единиц ресурса Si, затрачиваемого на изготовление единицы продукции Pj (числа aij – коэффициенты прямых затрат, которые называют технологическими коэффициентами); cj – прибыль от реализации единицы продукции Pj. Тогда математическая модель задачи оптимизации материальных инвестиционных ресурсов в общей постановке примет вид: найти такой план X=(x1, x2,…xn) выпуска продукции, удовлетворяющий системе
|
|
|
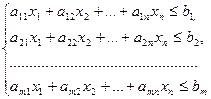
и условию
,
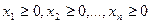при котором функция
принимает максимальное значение.
Задача оптимизации финансовых инвестиционных ресурсов.
Имеются два типа инвестиционных портфелей I и II, исходные данные и обозначения для постановки задачи приведены в таблице № 4 (цифры условные). Необходимо определить долю каждого в общем объеме инвестиций таким образом, чтобы инвестиционный риск был минимальным.
Таблица № 4
| Показатель | Обозначение | Значение (в долях) |
| Уровень средней доходности инвестиционных портфелей | Р0 | 0,045 |
| Математическое ожидание доходности инвестиционного портфеля I | ξ1 | 0,037 |
| Математическое ожидание доходности инвестиционного портфеля II | ξ2 | 0,068 |
| Ковариация доходности инвестиционных портфелей | Ω12 | 0,00623 |
Обозначим x1, x2 – доля инвестиционных портфелей соответственно I и II.
Причем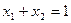 
(сумма долей инвестиционных портфелей должна составлять 1). Общий доход инвестиционных портфелей не должен превышать уровень средней доходности инвестиционных портфелей:
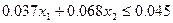
Переменные неотрицательные x1³0, x2³0.
Необходимо определить долу каждого инвестиционного портфеля так, чтобы ковариция уровня инвестиционного дохода по инвестиционным портфелям была бы минимальной:
.
Здесь ковариация представляет собой статистическую характеристику, иллюстрирующую меру сходства (или различий) двух инвестиционных ресурсов в динамике, амплитуде и направлении изменений. С помощью данного показателя оценивается уровень инвестиционного риска, чем меньше значение показателя ковариации, тем меньше уровень инвестиционного риска.
В качестве показателя уровня риска может быть использован показатель дисперсии. Дисперсия характеризует средний квадрат отклонений значений показателя от его среднего значения (или меру рассеивания).
Также уровень инвестиционного риска можно оценить с помощью показателя среднего квадратического (стандартного) отклонения. Данный показатель представляет собой положительное значение корня квадратного из дисперсии.
Необходимо заметить, что показатель ковариации для оценки уровня инвестиционного риска используется в случае анализа не более двух финансовых инструментов. Показатели дисперсии и стандартного отклонения используются для оценки уровня инвестиционного риска в случае анализа более чем двух финансовых инструментов. Тогда в качестве коэффициентов в целевой функции при переменных будут стоять соответствующие показатели дисперсий или стандартных отклоненй.
|
|
|
Математическая модель задачи оптимизации финансовых инвестиционных ресурсов в общей постановке примет вид. Найти доли инвестиционных портфелей xi удовлетворяющие ограничениям:
,
,
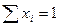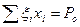и условию
,
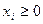при котором функция
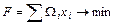
принимает минимальное значение.
Здесь приняты следующие обозначения:
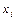- доля i – го финансового инструмента,
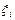- показатель дохода i – го финансового инструмента,
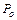- средняя норма доходности инвестиционных ресурсов,
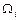- инвестиционный риск i – го финансового инструмента.
2 Реализация задач планирования инвестиционных процессов финансовых организаций средствами Microsoft Excel.
Для реализации построенных оптимизационных моделей инвестиционных процессов финансовых организаций в Microsoft Excel существует надстройка «Поиск решения».
«Поиск решения» доставляет не заранее известный конкретный результат для целевой функции, а отыскивает оптимальное (минимальное или максимальное) из возможных решение. Для сложных задач «Поиск решения» может генерировать множество различных решений. Шаблон задач планирования инвестиционных процессов, для решения которых можно воспользоваться надстройкой, должен иметь ряд общих свойств:
1. Существует единственная целевая ячейка, содержащая формулу.
2. Формула в целевой ячейке содержит ссылки (прямые или косвенные) на ряд изменяемых ячеек.
3. Может быть задано некоторое количество ограничений.
Прокомментируем решение задачи оптимизации распределения средств между инвестиционными объектами. Рассмотри первый пример. Первым действием необходимо ввести исходные данные. Введем на рабочий лист исходные данные как это показано на рис.3.1.
Рис.3.1 Шаблон решения задачи распределения инвестиционных средств
Вводим в диапазон С4:F6 коэффициенты инвестиционных затрат, в диапазон С3:F3 вводим инвестиционный спрос, в диапазон В4:В6 вводим мощности инвесторов.
Для формирования шаблона решения задачи необходимо ввести следующие расчетные формулы. Вводим в ячейку G9 формулу =СУММ(C9:F9), в ячейки G10:G11 копируем данную формулу методом протягивания (таким образом сформировано ограничение по мощностям инвесторов). Вводим в ячейку С12 формулу =СУММ(С9:С11), в ячейки D12:F12 копируем данную формулу методом протягивания (таким образом сформировано ограничение по инвестиционному спросу). Вводим в ячейку С14 формулу для расчета значения целевой функции (=СУММПРОИЗВ(C4:F6;C9:F11)). Для ввода формулы необходимо выполнить команды: Вставка/Функция/Математические/СУММПРОИЗВ. После чего заполнить окно диалога (рис. 3.2) по образцу.
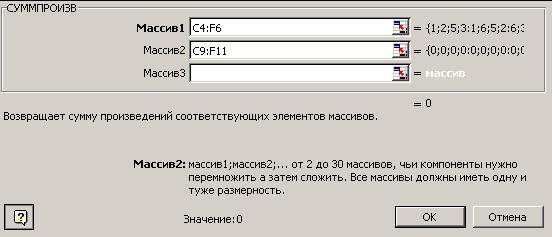
Рис. 3.2 Окно диалога формирования целевой функции
Далее обращаемся к надстройке Поиск решения с помощью команды меню Сервис. Но может быть так, что команда Поиск решения в этом меню отсутствует. Тогда необходимо выполнить следующую команду: Сервис / Надстройки, напротив Поиск решения поставить галочку. В результате произойдет активация команды Поиск решения.
Заполняем окно диалога как показано на рис. 3.3.
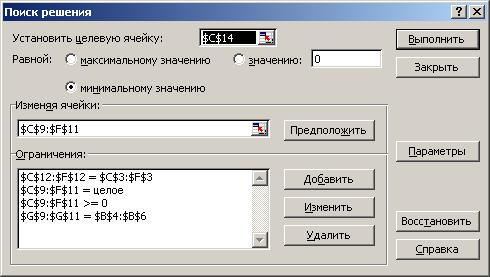
Рис. 3.3 Окно диалога «Поиск решения» задачи распределения инвестиционных средств
Устанавливаем целевую ячейку С14 равной минимальному значению. Изменяя ячейки C9:F11. Далее преступаем к вводу ограничений. Нажимаем кнопку Добавить и вводим ограничения как показано на рис. 3.4 – 3.8. Ввод следуещего ограничения осуществляется с помощью кнопки Добавить.
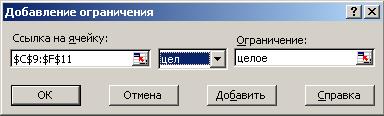
Рис.3.4
Рис. 3.5
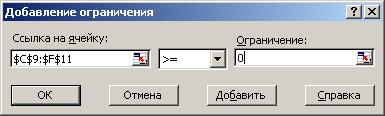
Рис. 3.6
Рис. 3.7
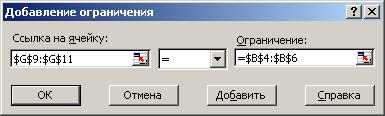
Рис. 3.8
Оптимальное решение получено после нажатия кнопки Выполнить. На рис. 3.9 в диапазоне C9:F11 указано оптимальное распределение инвестиционных вложений для каждой пары «инвестор – инвестиционный объект».
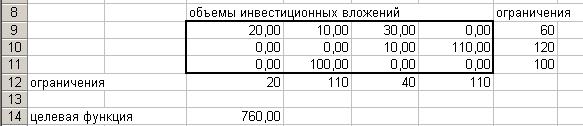
Рис.3.9 Оптимальное распределение инвестиционных вложений
Рассмотри второй пример. Введем на рабочий лист исходные данные как это показано на рис.3.10.
Рис. 3.10 Шаблон решения задачи распределения вложений в акции
Вводим в диапазон С4:F8 коэффициенты прибыли, в диапазон С3:F3 вводим инвестиционный спрос на акции, в диапазон В4:В8 вводим мощности инвесторов. Здесь добавлена фиктивная мощность 5-го инвестора в виде 5-й строки с нулевыми коэффициентами прибыли. Таким образом открытая задача приведена к закрытой.
Для формирования шаблона решения задачи необходимо ввести следующие расчетные формулы. Вводим в ячейку G11 формулу =СУММ(C11:F11), в ячейки G12:G15 копируем данную формулу методом протягивания (таким образом сформировано ограничение по мощностям инвесторов). Вводим в ячейку С16 формулу =СУММ(С11:С15), в ячейки D16:F16 копируем данную формулу методом протягивания (таким образом сформировано ограничение по инвестиционному спросу на акции). Вводим в ячейку С17 формулу для расчета значения целевой функции (=СУММПРОИЗВ(C4:F8;C11:F15)). Вызов функции осуществляется как и в предыдущем примере. Затем вызываем надстройку «Поиск решения». И заполняем окно диалога как показано на рис. 3.11.
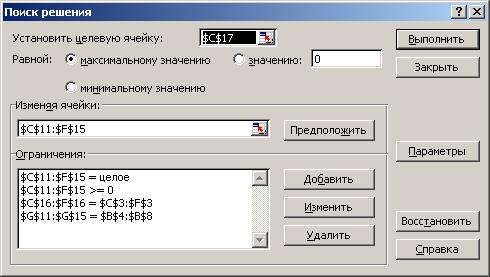
Рис. 3.11 Окно диалога «Поиск решения» задачи распределения вложений инвестиционных средств в акции
Устанавливаем целевую ячейку С17 равной максимальному значению. Изменяя ячейки C11:F15. Далее преступаем к вводу ограничений. Нажимаем кнопку Добавить и вводим ограничения как и в первом примере.
Оптимальное решение получено после нажатия кнопки Выполнить. На рис. 3.12 в диапазоне C11:F15 указано оптимальное распределение инвестиционных вложений в акции для каждой пары «инвестор – пакет акций».
Рис.3.12 Оптимальное распределение инвестиционных вложений в акции
|
|
|
