 |
Прокомментируем решение задачи оптимизации материальных инвестиционных ресурсов.
|
|
|
|
Первым действием необходимо ввести исходные данные. Введем на рабочий лист исходную таблицу с данными как это показано на рис.1.
Для формирования ограничений задачи в ячейку Е5 вводим функцию: СУММПРОИЗВ (C10:D10;C5:D5).
Вызов функции осуществляется следующими командами: Вставка – Функция – Математические – СУММПРОИЗВ - Массив 1 (C10:D10) (искомые значения плана производства) – Массив 2 (C5:D5) (ресурсы единицы продукции). Копируем функцию в ячейки С6:С8 с помощью маркера копирования.
В ячейку С11 вводим целевую функцию СУММПРОИЗВ (C10:D10;C9:D9).

Рис. 1
Перейдем теперь к постановке задачи для надстройки «Поиск решения». Для решаемой задачи целевой функцией будет функция в ячейке $С$11, изменяемыми данными – диапазон $С$10:$D$10, содержащий число видов продукции, диапазон $Е$5:$Е$8 – используется для определения ограничений задачи.
Для обращения к надстройке «Поиск решения» используется команда меню Сервис. Но может быть так, что команда Поиск решения в этом меню отсутствует. Тогда необходимо выполнить следующую команду: Сервис / Надстройки, напротив Поиск решения поставить галочку. После активации команды Поиск решения, необходимо заполнить окно диалога по образцу (рис.2).
Установить целевую ячейку $С$11 равной максимальному значению. Изменяя ячейки $С$10:$D$10. Для ввода ограничений нужно нажать кнопку Добавить.
1. Ограничения по ресурсам:
Ссылка на ячейку: = $Е$5:$Е$8, вид ограничения: <=, ограничение: ссылка на ячейку: = $В$5: $В$8. Добавить.
2. Ограничение на не отрицательность переменных:
Ссылка на ячейку: = $С$10:$D$10, вид ограничения: >=, ограничение 0. Добавить.
3. Ограничение на целостность переменных:
Ссылка на ячейку: = $С$10:$D$10, вид ограничения: цел. OК.
|
|
|

Рис. 2
После нажатия кнопки Выполнить надстройка «Поиск решения» приступает к итерациям, после вычислений открывает диалоговое окно Результаты поиска решения (рис.3), в котором выводится сообщение о решении задачи.

Рис. 3
Проанализируем решение. По результатам решения задачи необходимо производить продукции первого вида 6 ед., продукции второго вида – 4 ед., при этом инвестиционные затраты будут минимальными, а значение прибыли от инвестиционных вложений составит 24 единицы.
Если найденное решение устраивает, можно сохранить его на рабочем листе, выбрав Сохранить найденное решение. Можно также сохранить решение в качестве одного из сценариев с помощью кнопки Сохранить сценарий.
Прокомментируем решение задачи оптимизации финансовых инвестиционных ресурсов. Введем на рабочий лист исходные данные как это показано на рис.3.15

Рис. 3.15 Шаблон решения задачи оптимизации финансовых инвестиционных ресурсов
В ячейки А1:А7 вводим наименования показателей и переменных. В ячейки В1:В4 вводим значения показателей. В ячейки В6:В7 вводим обозначения переменных. В ячейку D2 вводим, начиная со знака равно, ограничение по уровню доходности инвестиционных портфелей (=В2*С6+В3*С7). В ячейку D3 вводим, начиная со знака равно, ограничение по доле инвестиционных портфелей (=С6+С7). Затем вызываем окно диалога «Поиск решения» и заполняем его по образцу (рис. 3.16).
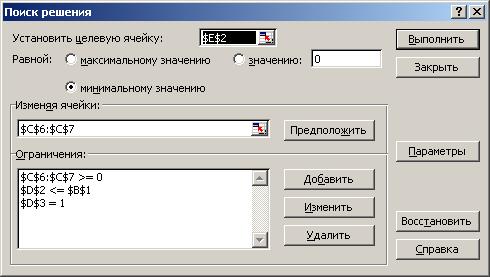
Рис. 3.16 Окно диалога «Поиск решения» задачи оптимизации финансовых инвестиционных ресурсов
Установить целевую ячейку Е2 равной минимальному значению. Изменяя ячейки С6:С7.
Вводим ограничения.
Ссылка на ячейку: = $С$6:$С$7, вид ограничения: = >=, ограничение 0.
Ссылка на ячейку: = $D$2, вид ограничения: = <=, ограничение $B$1.
Ссылка на ячейку: = $D$3, вид ограничения: =, ограничение 1.
В результате решения задачи (рис. 3.17) получили следующие данные. Оптимальная доля инвестиционного портфеля I составляет 74%, доля инвестиционного портфеля II составляет 26%, значение риска составило 0,62%.
|
|
|

Рис. 3.17 Результаты поиска решения задачи оптимизации финансовых инвестиционных ресурсов
|
|
|


