Использование номограмм Честната-Майера

Санкт-Петербургский государственный

электротехнический университет «ЛЭТИ»

 

 

Динамический синтез следящей системы

 

 

Учебно-методическое пособие к курсовой работе

по дисциплине «Теория автоматического управления»

 

 

Санкт-Петербург

Издательство СПбГЭТУ «ЛЭТИ»

УДК 519.71(075.9)

 

 

Второв В. Б. Динамический синтез следящей системы: Учебно-методическое пособие к курсовой работе по дисциплине «Теория автоматического управления». СПб.: Издательство СПбГЭТУ «ЛЭТИ», 2017. 40 с.

 

 

Содержит основные требования и методику выполнения курсовой работы, необходимые расчетные соотношения и практические рекомендации по выбору элементов для обеспечения заданных точности и динамических свойств следящей системы.

Предназначено для студентов направления 27.03.04 «Управление в технических системах» факультета электротехники и автоматики.

 

 

Утверждено

редакционно-издательским советом университета

в качестве методических указаний

 

 

© СПбГЭТУ «ЛЭТИ», 2017

ПРЕДИСЛОВИЕ

 

Настоящие методические указания представляют собой пересмотренный вариант предыдущего издания 2004 г. [1]. Они содержат все необходимые для успешного выполнения курсовой работы пояснения и практические рекомендации относительно содержания и методики выполнения курсовой работы.

Выполнение курсовой работы имеет своей целью овладение студентами методикой и инженерными навыками динамического синтеза следящей системы. Последний заключается в таком выборе структуры и параметров управляющей части системы (что обычно достигается введением в исходную систему некоторых корректирующих средств), при котором следящая система кроме необходимых показателей точности приобретает требуемые динамические свойства.

В данной курсовой работе для выполнения динамического синтеза рекомендуется использовать метод логарифмических частотных характеристик, нашедший наиболее широкое применение в инженерной практике в силу своей наглядности, простоты и универсальности применения для целей анализа и синтеза. Вместе с тем, частотные методы расчета автоматических систем недостаточно формализованы, в связи с чем процедура синтеза, как правило, носит итерационный характер. К тому же рекомендуемые обычно довольно громоздкие методики синтеза желаемой логарифмической амплитудной частотной характеристики [2] нередко дают весьма неточные результаты. В связи с этим в данной курсовой работе студентам рекомендуется применять упрощенную методику (вполне приемлемую по точности), дополняя процедуру синтеза компьютерным анализом показателей качества желаемой системы.

Для анализа динамических свойств синтезированной системы в курсовой работе предусматривается использование ЭВМ.

 

 

1. СОДЕРЖАНИЕ КУРСОВОЙ РАБОТЫ

Курсовая работа «Динамический расчет следящей системы» должна содержать следующие обязательные элементы.

1. Титульный лист и задание (оформляются в соответствии с прил. 1 и 2.

2. Оглавление.

3. Введение, где должны быть изложены цель и основные задачи работы, используемые теоретические методы и обоснование их выбора.

4. Описание системы и анализ ее динамических свойств.

Здесь должны быть приведены:

а) сведения о назначении системы, ее структурная схема и параметры;

б) построение логарифмических частотных характеристик (ЛЧХ) исходной (нескорректированной) системы и анализ ее устойчивости.

5. Построение желаемой логарифмической амплитудной частотной характеристики (ЛАХ) разомкнутой системы, включающее в себя:

а) построение низкочастотной части желаемой ЛАХ;

б) построение средне- и высокочастотной частей желаемой ЛАХ;

в) анализ переходной характеристики, частотных характеристик и точности желаемой системы на ЭВМ и, при необходимости, коррекцию желаемой ЛАХ.

6. Синтез корректирующего устройства, предусматривающий:

а) выбор способа коррекции по согласованию с преподавателем (как правило, используется параллельная коррекция);

б) построение ЛАХ корректирующего устройства и ее уточнение с целью обеспечить физическую реализуемость;

в) определение ЛАХ скорректированной системы приближенным методом (построение асимптотической ЛАХ) и точным методом (на ЭВМ); сравнение с желаемой ЛАХ;

г) определение состава элементов корректирующего устройства (включая измерительно-преобразовательные элементы), разработка принципиальной схемы и расчет параметров корректирующего устройства; определение его передаточной функции.

7. Исследование динамических свойств скорректированной системы на ЭВМ. Предусматриваются следующие этапы:

а) получение переходной характеристики системы;

б) определение показателя колебательности (для варианта M);

в) оценка чувствительности заданных показателей качества динамики к вариациям параметров системы.

8. Анализ точности системы при отработке типовых входных воздействий.

9. Заключение (анализ полученных в курсовой работе результатов и их сопоставление с требованиями задания).

10. Библиографический список.

 

 

2. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ

Курсовая работа выполняется на листах формата А4 с полями (левое – шириной не менее 2,5–3 см). Ее оформление должно соответствовать ГОСТ 7.32 – 2001. Не разрешается вставлять листы в «файлики» и затем подшивать. Не рекомендуется использовать толстые скоросшиватели.

Работа пишется от руки, разборчивым почерком на одной стороне листа. На принтере печатаются только результаты компьютерного моделирования (графики, схемы в Simulink), а также титульный лист, задание и, возможно, оглавление. Графики ЛАХ должны быть выполнены на миллиметровой бумаге. Схемы могут быть выполнены также на миллиметровой бумаге с соблюдением требований ЕСКД.

Строго обязательны пояснения в тексте: расшифровка всех используемых обозначений, объяснение и обоснование всех действий и способа их выполнения. Буквенные обозначения физических величин должны соответствовать ГОСТ. Числа, являющиеся результатами вычислений, округляются, как правило, до трёх значащих цифр (если первая значащая цифра – единица, то в числе надо оставить четыре значащих цифры). При вычислениях приводится расчетная формула, затем подставляются все необходимые численные значения и, наконец, записывается окончательный числовой результат в необходимой размерности. Расчеты выполняются в СИ.

Все страницы должны быть пронумерованы. Следует пронумеровать формулы, на которые есть ссылки в тексте, все иллюстрации и таблицы. Желательно, чтобы иллюстрации имели подписи и приводились по ходу изложения материала; в тексте на них необходимо сделать ссылки.

Ссылки на литературный источник даются заключенным в квадратные скобки числом, соответствующим номеру данного источника в библиографическом списке. Последний должен содержать полные библиографические описания использованных при выполнении курсовой работы литературных источников.

3. ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

3.1. Общие положения

Задание на курсовую работу выдается студенту преподавателем и, в соответствии с номером варианта, содержит данные из двух таблиц (таблицы вариантов находятся у преподавателя).

Первая таблица содержит численные значения параметров элементов системы, вторая – требования к качеству проектируемой системы. Эти требования делятся на две группы:

1) требования к точности;

2) требования к показателям качества динамики.

Предусмотрены два варианта требований к точности воспроизведения задающего воздействия: А – для гармонического воздействия, Б – для воздействия произвольной формы. Требования к динамике также имеют две разновидности; они условно обозначены: М, если задан показатель колебательности системы М, и h, если заданы показатели качества переходной характеристик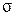и и . Содержательное описание обеих групп требований приводится в подразделах 3.1 и 3.2.

На титульном листе студент должен указать номер варианта своего задания, состоящий из трех позиций:

– порядковый номер варианта;

– вид требований к точности (А или Б);

– вид требований к динамике (М или h);

например: вариант 15А h.

3.1. Требования к точности

Вариант А. Входное (задающее) воздействие – гармоническое (например, при компенсации качки):

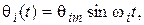(3.1)

где – амплитуда входного воздействия, 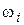– круговая частота.

Необходимо, чтобы при отработке воздействия (3.1) амплитуда установившейся ошибки не превышала допустимого значения . Здесь ошибка , где 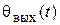– выходная переменная – угол поворота исполнительной оси.

Значения 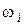, и 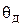заданы.

Вариант Б. Входное воздействие имеет произвольную форму, но скорость его изменения и ускорение ограничены:

, , (3.2)

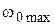где и 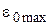– соответствующие максимально допустимые значения.

Необходимо, чтобы при отработке воздействия, удовлетворяющего условиям (3.2), установившаяся ошибка не превышала допустимого значения .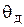

Значения 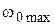, 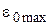и заданы.

 

3.2. Требования к динамике

Вариант М. Показатель колебательности спроектированной системы не должен превышать заданного значения M.

Вариант h. Перерегулирование переходной характеристики и время регулирования системы не должны превышать заданных значений и .

Задание на курсовую работу должно быть оформлено в соответствии с прил. 2.

В курсовой работе должны быть выбраны и рассчитаны все основные элементы следящей системы. Расчет ведется в предположении, что система представляет собой линейную непрерывную динамическую систему с постоянными сосредоточенными параметрами.

 

4. ОПИСАНИЕ ИСХОДНОЙ СИСТЕМЫ

4.1. Структурная схема системы

Выполнение курсовой работы рекомендуется начать с составления структурной схемы, на которой изображаются лишь основные функциональные блоки системы. Их названия даются в виде аббревиатур, смысл которых затем поясняется, например:

ЧЭ – чувствительный элемент;

У1 – первый предварительный усилитель и т. п.

Далее должна быть приведена аналитическая структурная схема системы. На ней внутри блоков записываются передаточные функции в буквенном виде с последующим указанием численных значений всех параметров. На схеме следует обозначить все переменные системы.

Исходная система, в дальнейшем именуемая также нескорректированной, представляет собой следящую систему, состоящую из следующих последовательно соединенных функциональных элементов:

· чувствительный элемент (ЧЭ) (например, на основе вращающихся трансформаторов или потенциометрического моста); выполняет функцию сравнения задающего воздействия 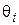и регулируемой переменной 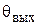и формирует сигнал, пропорциональный ошибке 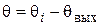; описывается коэффициентом передачи .

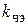· усилительно-преобразовательное устройство (УПУ) (может содержать фазочувствительный выпрямитель или демодулятор; обязательно содержит один или несколько предварительных усилителей, обеспечивающих требуемое значение добротности системы и возможность суммирования сигнала местной обратной связи, т. е. введение параллельной коррекции), описывается коэффициентом передачи 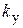; выходное напряжение УПУ обозначается .

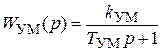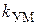· усилитель мощности (УМ) (транзисторный усилитель, тиристорный преобразователь или широтно-импульсный преобразователь); описывается передаточной функцией (ПФ) , где и 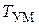– соответственно коэффициент передачи и постоянная времени УМ; выходное напряжение УМ обозначается ;

· двигатель постоянного тока Д; описывается ПФ 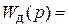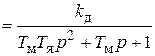, где 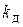– коэффициент передачи двигателя по скорости (угловая скорость считается выходной переменной), – электромеханическая постоянная времени привода (двигателя с механизмом и редуктором), – электромагнитная постоянная времени якорной цепи двигателя;

· редуктор; описывается ПФ 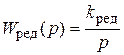, где – коэффициент передачи; выходная переменная редуктора (угол поворота выходного вала) обозначается .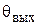

4.2. Расчет и анализ исходной системы

Этот раздел курсовой работы предполагает выполнение следующих действий.

1. Определить требуемую добротность системы 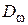по формулам, соответственно для вариантов А и Б:

, (4.1)

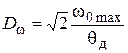. (4.2)

2. Определить необходимый коэффициент усиления предварительного усилителя (ПУ) (а точнее, УПУ) по формуле

.

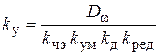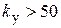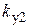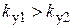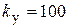3. Определить число операционных усилителей (ОУ), необходимых для реализации коэффициента передачи . Коэффициент усиления одного ОУ не должен превышать 100. Если , целесообразно использовать два ОУ с коэффициентами усиления и (), причем следует назначить (лучше ; например, если , то 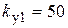, ). Операционный усилитель, если он единственный, или второй операционный усилитель, если их два, будет также выполнять функцию суммирования сигнала местной (корректирующей) обратной связи. Если , то разбиение этого коэффициента на два все равно целесообразно (в этом случае следует взять ), поскольку на охваченном корректирующей обратной связью операционном усилителе необходимо будет реализовать еще дополнительный коэффициент усиления, обеспечивающий выполнение частотного условия эквивалентности последовательного и параллельного корректирующих устройств (см. 7.3).

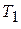5. Преобразовать ПФ двигателя. Соотношение постоянных времени и в задании таково, что двигатель описывается апериодическим звеном 2-го порядка с постоянными времени и . Необходимо определить их значения.

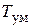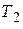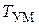6. Упростить ПФ силовой части (СЧ). Поскольку постоянные времени и сравнительно малы, то соответствующие им апериодические звенья 1-го порядка можно приближенно заменить одним апериодическим звеном 1-го порядка с постоянной времени , равной сумме постоянных времени и 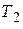. Тогда ПФ СЧ

,

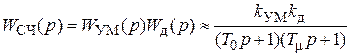где , .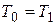

7. Изобразить окончательную структурную схему системы, выделив в ней следующие элементы: ЧЭ, ПУ (или оба ПУ, если их два), СЧ и редуктор, записав их ПФ в числовом виде.

8. Записать ПФ нескорректированной разомкнутой системы 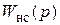в буквенном и числовом виде.

9. Записать в числовом виде ПФ замкнутой системы .

10. По критерию Гурвица исследовать, устойчива нескорректированная система или нет.

11. Изобразить асимптотическую ЛАХ нескорректированной системы по ее передаточной функции в разомкнутом состоянии. Этот график, необходимый для синтеза корректирующей цепи, строят на обычной (не полулогарифмической) миллиметровой бумаге. Рекомендации по построению этой ЛАХ приведены в прил. 3).

12. Получить на компьютере графики точной ЛАХ и ЛФХ разомкну­той системы. С помощью критерия Найквиста исследовать устойчивость системы. Если система устойчива, определить ее запас устойчивости по фазе и сделать суждение о предполагаемом качестве переходных процессов.

 

5. ПОСТРОЕНИЕ ЖЕЛАЕМОЙ ЛАХ СЛЕДЯЩЕЙ СИСТЕМЫ

Желаемую ЛАХ разомкнутой системы принято разделять на три части: низкочастотную (НЧ), среднечастотную (СЧ) и высокочастотную (ВЧ) (рис. 1).

НЧ-часть ЛАХ строится из условия обеспечения требуемой точности, СЧ-часть – из условий обеспечения устойчивости системы и требуемых значений ее показателей качества, а ВЧ-часть незначительно влияет на по-

 

 

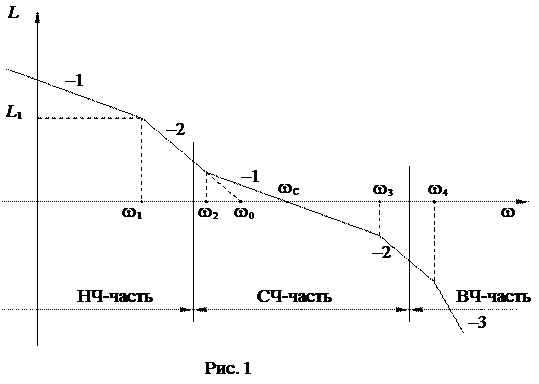казатели работы системы, в связи с чем при проектировании системы стремятся повторить в ВЧ-части желаемой ЛАХ основные особенности ВЧ части ЛАХ нескорректированной системы, чтобы излишне не усложнять коррекцию.

 

5.1. Низкочастотная часть желаемой ЛАХ

Для выполнения требований в отношении точности достаточно, чтобы по задающему воздействию система имела астатизм первого порядка. Типичный вид ЛАХ такой системы показан на рис. 1. Числами –1...–3 обозначена кратность наклона участков ЛАХ значению 20 дБ/дек. Приведенный тип ЛАХ можно, таким образом, условно обозначить как –1/–2/–1/–2/–3. Возможны и другие типы желаемой ЛАХ. Некоторые методики частотного синтеза рассчитаны на типовые ЛАХ, состоящие из четырех участков, например –1/–2/–1/–3 или –1/–3/–1/–3, с тремя сопрягающими частотами. Эти методики можно применять и для показанной на рис. 1 характеристики, если участок с наклоном –2, выполняющий сопряжение СЧ и ВЧ участков, имеет небольшую протяженность (до 0.2–0.3 дек). В этом случае в качестве частоты следует рассматривать частоту пересечения третьего и пятого участков ЛАХ.

Методика построения НЧ-части желаемой ЛАХ имеет некоторые различия для вариантов А и Б.

Вариант А. Основное требование состоит в том, чтобы точная (не асимптотическая!) ЛАХ следящей системы не проходила ниже контрольной точки A (рис. 2, а) с координатами (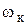, ), где частота 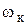равна частоте входного гармонического воздействия 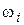, а ордината , дБ определяется выражением

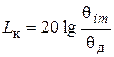. (5.1)

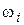Обычно в качестве первой частоты сопряжения принимают частоту , как на рис. 2, а. Это связано с тем, что при других вариантах расположения НЧ-части (на рис. 2, а они показаны штриховыми линиями) возникают осложнения: если 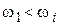, то добротность системы оказывается завышенной по сравнению с расчетным значением, определяемым выражением (4.1), и, следовательно, требуются завышенные значения коэффициентов усиления предварительных усилителей; если же , то могут возникнуть трудности с сопряжением НЧ- и СЧ-частей ЛАХ, синтезируемых на основе различных требований.

 

 

С учетом изложенного рекомендуется следующий порядок построения НЧ-части желаемой амплитудной характеристики.

1. Определить по формуле (5.1).

2. Построить контрольную точку 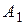с координатам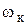и и , дБ (ординаты точной и асимптотической ЛАХ на сопрягающей частоте отличаются на 3 дБ).

3. Через контрольную точку провести асимптоты с наклонами –20 и – 40 дБ/дек.

Рекомендуется после этого графически определить по построенной НЧ-части значение добротности и убедиться, что оно совпадает со значением, найденным по формуле (4.1).

Вариант Б. Входное воздействие произвольной формы с ограниченными скоростью изменения и ускорением должно быть пересчитано на эквивалентное гармоническое

по формулам

; .

Основное требование, налагаемое на НЧ-часть ЛАХ, состоит в том, что ее точный график не должен заходить в запретную область, граница которой отмечена штриховкой на рис. 2, б. Ордината точки А определяется формулой

. (5.2)

Порядок построения НЧ-части ЛАХ следующий.

1. Определить 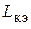по формуле (5.2).

2. Построить контрольную точку (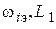), где 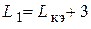, дБ.

3. Провести через нее асимптоты с наклонами –20 и –40 дБ/дек.

Как и в предыдущем случае, рекомендуется по графику ЛАХ определить значение добротности системы и сравнить со значением, найденным по формуле (4.2).

 

5.2. Средне- и высокочастотная части желаемой ЛАХ

Вариант М. Наиболее простой способ построения СЧ-части по заданному значению показателя колебательности предусматривает следующую последовательность действий.

1. Определить частоту 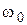пересечения продолжения второго участка ЛАХ с осью частот (см. рис. 1) графически или по формуле

.

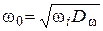2. Найти сопрягающую частоту как

.

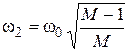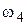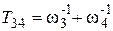3. Задаться значениями сопрягающих частот и с учетом ограничения , где , а

.

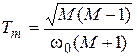Не следует сильно занижать значение 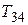по сравнению со значением , так как это может повлечь за собой необходимость реализации завышенных значений коэффициентов усиления схемы управляющей части системы, а также снизит ее помехозащищенность. По той же причине нежелательно, чтобы частота 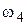превышала частоту более чем в 2–2,5 раза. Например, если принять , то , 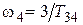(рекомендуемый вариант). Можно также выбрать (ЛАХ типа –1/–2/–1/–3). Иногда для упрощения процедуры синтеза или вида корректирующей цепи выбирают одну из указанных частот равной какой-либо сопрягающей частоте ЛАХ нескорректированной системы.

4. На частотах , и 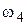произвести изломы ЛАХ в соответствии с рис. 1.

Таким образом, желаемая ЛАХ следящей системы оказывается полностью сформирована. Для последующего выполнения синтеза корректирующего устройства необходимо на лист с графиком желаемой ЛАХ нанести также график ЛАХ нескорректированной системы. Необходимо помнить, что начальные участки обеих характеристик должны совпадать; кроме того, эти ЛАХ должны иметь одинаковые наклоны последнего участка.

Вариант h. Частотные методы синтеза желаемой ЛАХ по заданным значениям перерегулирования и времени регулирования отличаются значительным разнообразием. Рассмотрим наиболее употребительные из них.

Метод В.В.Солодовникова

Он может быть применен в тех случаях, когда требуется спроектировать систему с перерегулированием не менее 18 %. Как показывает практика, показатели качества системы с ЛАХ, синтезированной данным методом, часто существенно отличаются от значений, используемых в качестве исходных данных при синтезе. Это объясняется тем, что используемые в рассматриваемом методе соотношения между показателями качества переходной характеристики и некоторыми параметрами частотных характеристик системы предполагают, что вещественная частотная характеристика замкнутой системы имеет вполне определенный типовой вид и удовлетворяет некоторым количественным требованиям, чего гарантировать заранее, естественно, нельзя. Построение желаемой ЛАХ по методу Солодовникова выполняется в следующем порядке.

1. Определение частоты среза . Ее значение следует задать равным или несколько превышающим значение, найденное по номограмме [2, рис. 7.5]. По заданному значению перерегулирования с помощью кривой 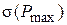номограммы определяют соответствующее значение 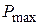. Затем по значению 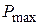с помощью кривой 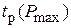определяют значение коэффициента c в равенстве 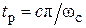. Поскольку значение задано, из последнего равенства находят .

В некоторых справочниках и учебниках вместо величины 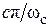на номограмме указывается 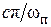, где 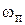есть верхняя граница интервала частот, где вещественная характеристика положительна. В этом случае сначала указанным ранее способом находят 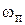, после чего задают частоту среза как 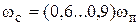. Заметим, что частоту среза можно определять и по приближенной формуле, используемой в изложенной далее упрощенной методике.

2. Построение среднечастотной асимптоты. Ее проводят через точку на оси абсцисс с наклоном –20 дБ/дек.

3. Сопряжение среднечастотной асимптоты с НЧ-частью ЛАХ. Его выполняют с помощью асимптоты с наклоном –40 (иногда –60) дБ/дек, причем так, чтобы в интервале частот, где , имелся избыток фазы (превышение значения –180˚)

. (5.3)

Значения и 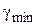определяют с помощью номограммы, приведен-ной, например, в [2], по ранее найденному значению 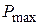. Однако указанные величины можно найти и иначе – с помощью приводимой во многих справочниках номограммы для определения вещественной частотной характеристики системы с единичной обратной связью по ЛЧХ разомкнутой системы. На указанной номограмме находят две кривые, соответствующие значениям 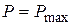и , и заключают их в прямоугольник. Его размерами будут удвоенные значения искомых величин.

Практически сопряжение СЧ- и НЧ-частей ЛАХ выполняют следующим образом. Сначала ограничивают СЧ-участок точкой, для которой значение ЛАХ составляет 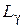. Если СЧ-участок не пересекся с НЧ-частью, то следует продлить его до пересечения со второй асимптотой. Если же он пересекся с НЧ-частью, то, в общем случае, необходимо сместить СЧ-участок вправо – так, чтобы его граничная точка попала на вторую асимптоту. Далее надо оценить избыток фазы в точке сопряжения СЧ- и НЧ-частей ЛАХ (т. е. на частоте ). Он должен удовлетворять условию (5.3). Для определения значения фазы рекомендуется (как в данном случае, так и в аналогичных ситуациях на этапе синтеза желаемой ЛАХ и приближенного анализа качества системы) использовать формулу [3] для приближенной оценки значения ЛФХ минимально-фазовой системы по ее ЛАХ:

, (5.4)

где 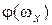– значение фазы в градусах на частоте , а – перепад ЛАХ (дБ) на интервале в две декады с частотой посередине.

Обычно условие (5.3) легко выполняется. Если избыток фазы превышает значение 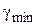более чем на 5...10º, то для повышения точности синтеза рекомендуют уменьшить избыток фазы, для чего следует сместить вторую асимптоту вправо (идя тем самым на сокращение СЧ-участка) или увеличить ее наклон, что менее желательно, так как приведет к усложнению коррекции.

4. Сопряжение среднечастотной асимптоты с ВЧ-частью ЛАХ. СЧ-участок с наклоном –20 дБ/дек необходимо ограничить справа точкой, для которой значение ЛАХ составляет (частота 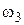). После этого надо сформировать ВЧ-часть желаемой ЛАХ, выполнив изломы на частотах 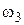и 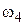. Метод требует, чтобы в интервале частот, в котором 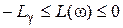, удовлетворялось неравенство (5.3). Обычно его трудно выполнить, но следует, по крайней мере, стремиться обеспечить максимальный избыток фазы на частоте 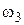, для чего рекомендуется в разумных пределах увеличивать протяженность участка с наклоном –40 дБ/дек.

Использование номограмм Честната-Майера

Для построения СЧ- и ВЧ-частей желаемой ЛАХ могут быть использованы номограммы Честната-Майера [4], позволяющие для систем, имеющих характерные (типовые) ЛАХ с четырьмя участками, определять основные показатели качества переходной характеристики и амплитудной частотной характеристики замкнутой системы. Для синтеза желаемой ЛАХ эти номограммы используются следующим образом.

1. Задаются типом желаемой ЛАХ. В данной курсовой работе следящая система рассматривается как динамическая система третьего порядка, поэтому целесообразно выбрать характеристику типа –1/–2/–1/–3 (при необходимости по окончании синтеза можно выполнить сопряжение двух последних асимптот небольшим участком с наклоном –40 дБ/дек).

2. Задаются отношением 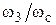, выбрав его из ряда 1, 2, 4, 8 и ∞.

3. По результатам пп. 1 и 2 выбирают соответствующую пару номограмм, расположенных одна под другой.

4. По заданному значению перерегулирования определяют относительное значение максимума переходной характеристики (в [4] эта величина обозначена как ). Например, если , то .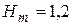

5. По построенной НЧ-части желаемой ЛАХ определяют значение 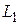ординаты на первой сопрягающей частоте (см. рис. 1).

6. Для данного значения по верхней номограмме находят значение 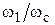. Для этого в соответствии со значением 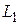выбирают на номограмме нужный график. Поскольку графики даны только для дискретного ряда значений 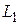(80, 60, 40, 30 и 20 дБ), обычно требуется интерполяция.

7. Так как значение 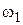известно по результатам синтеза НЧ-части, по 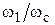находят значение частоты среза .

8. Для найденного значения 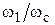по нижней номограмме (выбрав график, соответствующий значению 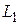) определяют значение отношения , откуда по известному значению находят фактическое значение времени регулирования . Последнее сравнивают со значением, указанным в задании на курсовую работу.

9. Если найденное значение времени регулирования превышает заданное, следует попытаться добиться желаемого результата, повторив расчет для другого значения 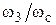. Если это не удается, необходимо увеличить значение частоты среза.

10. Через точку на оси абсцисс графика ЛАХ, соответствующую найденному значению , проводят асимптоту с наклоном –20 дБ/дек: влево – до пересечения с НЧ-частью ЛАХ, вправо – до частоты .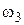

11. От последней точки проводят вправо высокочастотную асимптоту с наклоном –60 дБ/д

12	Поделиться:

Воспользуйтесь поиском по сайту: