 |
Принцип максимизации выпуска и минимизации издержек.
|
|
|
|
Пусть нам дана конкретная технология производства продукта:
Q=K 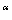 L
L 
а также мы имеем стоимостное ограничение на ресурсы:
C=rK+wL,
где r – арендная плата за оборудование, а w – ставка заработной платы. Тогда данная задача формулируется так:
(максимизация выпуска)
 (при заданном ограничении)
(при заданном ограничении)
Т.к. это задача на условный экстремум (есть целевая функция, есть уравнение ограничения), то можно выписать функцию Лагранжа:
F(K,L,  )= K
)= K 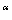 L
L  +
+ 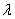 (C-rK-wL)
(C-rK-wL)
Выпишем условия первого порядка:

Имеем систему из трех уравнений с тремя неизвестными. Для удобства решения разделим первое уравнение на второе.
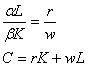
Из этой системы находим K и L, т.е. в данном случае такую конфигурацию ресурсов, при которой достигается максимальный выпуск.
K= 
L= 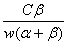
Q=(  )
)  (
(  )
)  =
= 
K и L есть в данном случае функции спроса на ресурсы, зависящие от C, r, и w. Величина Q есть в данном случае максимальный выпуск, которого достигает фирма в точке (K,L)=(  ,
, 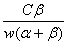 ). Q есть функция условного предложения фирмы.
). Q есть функция условного предложения фирмы.
Предположим, что у нас имеется два фактора производства с ценами w 1 Ошибка! Не указан аргумент ключа. и w 2 Ошибка! Не указан аргумент ключа. и мы хотим найти самый дешевый способ производства заданного объема выпуска y. Если обозначить используемые количества каждого из двух факторов через x 1 и x 2 Ошибка! Не указан аргумент ключа., а производственную функцию для фирмы — через f (x 1, x 2) Ошибка! Не указан аргумент ключа.Ошибка! Не указан аргумент ключа., то эту задачу можно записать в виде
min w 1 x 1 + w 2 x 2
x 1, x 2 Ошибка! Не указан аргумент ключа.
при f (x 1, x 2) Ошибка! Не указан аргумент ключа. = y.
При проведении подобного рода анализа следует сделать те же предупреждения, что и в предыдущей главе: убедитесь, что вы включили в подсчет издержек все издержки производства и что все измерения производятся в совместимом временном масштабе.
|
|
|
Решение этой задачи минимизации издержек — величина минимальных издержек, необходимых для достижения определенного объема выпуска, — будет зависеть от w 1, w 2 и y, поэтому мы запишем это решение как c (w 1, w 2, y H) Ошибка! Не указан аргумент ключа.. Эта функция известна как функция издержек, и она будет представлять для нас значительный интерес. Функция издержек c (w 1, w 2, y J) Ошибка! Не указан аргумент ключа. показывает минимальные издержки производства y единиц выпуска при ценах факторов, равных (w 1, w 2 Ошибка! Не указан аргумент ключа.).
Чтобы понять решение этой задачи, изобразим функцию издержек и технологические ограничения для фирмы на одном графике. Изокванты дают нам технологические ограничения — все комбинации x 1 и x 2 Ошибка! Не указан аргумент ключа., с помощью которых можно произвести y.
Предположим, что мы хотим нанести на график все комбинации факторов, дающие один и тот же уровень издержек C. Мы можем записать это в виде выражения
w 1 x 1 + w 2 x 2 = C
которое может быть преобразовано в
x 2 = 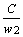 —
—  x 1
x 1
Легко увидеть, что это уравнение прямой, имеющей наклон — w 1/ w 2 и точку пересечения с вертикальной осью C / w 2. Изменяя число C, мы получаем целое семейство изокост. Каждая точка изокосты выражает одни и те же издержки C, и более высокие изокосты связаны с большими издержками.
Таким образом, наша задача минимизации издержек может быть перефразирована следующим образом: найти на изокванте точку, с которой связана самая низкая изокоста. Такая точка показана на рис.19.1.
Обратите внимание на то, что если оптимальное решение предполагает использование некоторого количества каждого из факторов и если изокванта представляет собой гладкую кривую, то точка минимизации издержек будет характеризоваться условием касания: наклон изокванты должен быть равен наклону изокосты. Или, пользуясь терминологией гл.17, технологическая норма замещения должна равняться отношению цен факторов:
|
|
|
— 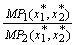 = TRS(
= TRS( 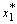 ,
, 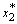 ) = —
) = — 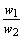 . (19.1)
. (19.1)
(В случае краевого решения, когда один из двух факторов не используется, условие касания удовлетворяться не должно. Аналогичным образом, если производственная функция имеет "изломы", условие касания теряет смысл. Эти исключения подобны исключениям в ситуации с потребителем, поэтому в настоящей главе мы не будем акцентировать внимание на указанных случаях.)
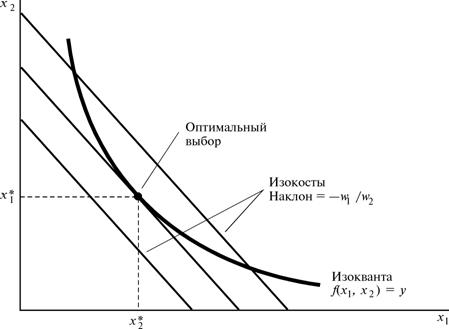
| Рис. 19.1 | Минимизация издержек. Выбор количеств факторов, минимизирующих издержки производства, может определяться нахождением на изокванте точки, связываемой с самой низкой изокостой. |
Алгебра, скрывающаяся за уравнением (19.1), трудностей не представляет. Рассмотрим любое изменение структуры производства (D x 1, D x 2S), при котором выпуск остается постоянным. Такое изменение должно удовлетворять уравнению:
MP 1( 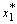 ,
, 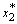 )D x 1 + MP 2(
)D x 1 + MP 2( 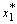 ,
, 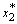 )D x 2 = 0. (19.2)
)D x 2 = 0. (19.2)
Обратите внимание на то, что D x 1T и D x 2U должны иметь противоположные знаки; если вы увеличиваете используемое количество фактора 1, то для сохранения выпуска неизменным вам придется уменьшить используемое количество фактора 2.
Если мы находимся в точке минимума издержек, то данное изменение не может привести к снижению издержек, поэтому должно соблюдаться условие:
w 1D x 1 + w 2D x 2 ³ 0. (19.3)
Теперь рассмотрим изменение (—D x 1, —D x 2VW), при котором также производится постоянный объем выпуска и издержки также не могут снижаться. Это подразумевает, что
— w 1D x 1 — w 2D x 2 ³ 0. (19.4)
Сложив выражения (19.3) и (19.4), получим
w 1D x 1 + w 2D x 2 = 0. (19.5)
Решение уравнений (19.2) и (19.5) для D x 2/D x 1X дает нам
 = —
= — 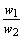 = —
= — 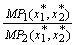 ,
,
а это не что иное, как условие минимизации издержек, выведенное выше путем геометрических рассуждений.
Обратите внимание на некоторое сходство рис. 19.1 с решением задачи потребительского выбора, графически изображенным ранее. Хотя эти решения и выглядят одинаково, на самом деле они относятся к разным задачам. В задаче потребительского выбора прямая являлась бюджетным ограничением, и потребитель в поисках наиболее предпочитаемого положения двигался вдоль бюджетного ограничения. В задаче с производителем изокванта представляет собой технологическое ограничение, и производитель в поисках оптимального положения перемещается вдоль изокванты.
|
|
|
Выбор количеств факторов, минимизирующих издержки фирмы, вообще говоря, зависит от цен факторов и от того объема выпуска, который фирма хочет производить, поэтому мы записываем эти выбранные количества факторов в виде x 1(w 1, w 2, y Y)Z и x 2(w 1, w 2, y AA)BB. Это так называемые функции условного спроса на факторы, или функции производного спроса на факторы. Они показывают взаимосвязь между ценами и выпуском и оптимальный выбор фирмой количества факторов при условии производства фирмой заданного объема выпуска y.
Обратите особое внимание на различие между функциями условного спроса на факторы и функциями спроса на факторы, максимизирующего прибыль, которые были рассмотрены в предыдущей главе. Функции условного спроса на факторы показывают выбор, минимизирующий издержки при заданном объеме выпуска; функции же спроса на факторы, максимизирующего прибыль, показывают выбор, максимизирующий прибыль при заданной цене фактора.
Функции условного спроса на факторы, как правило, не являются непосредственно наблюдаемыми: они представляют собой гипотетическое построение и отвечают на вопрос, сколько каждого фактора использовала бы фирма, если бы хотела произвести заданный объем выпуска самым дешевым способом. Однако функции условного спроса на факторы полезны в качестве способа отделения задачи определения оптимального объема выпуска от задачи определения метода производства, минимизирующего издержки.
|
|
|


