Главная | Обратная связь | Поможем написать вашу работу!

Построение аддитивной модели

Лабораторная работа № 4. Аддитивная и мультипликативная модели временного ряда

Задание

На сайте www.gks.ru или любом другом выбрать временной ряд по одному из социально-экономических показателей, содержащий сезонную составляющую. Можно выбрать данные, имеющие отношение к вашей курсовой или дипломной работе, тогда результат этой лабораторной работы вы сможете использовать в этих работах!

1. Постройте график данного временного ряда. Охарактеризуйте структуру этого ряда (есть ли тренд, сезонность, период сезонной компоненты).

2. Постройте аддитивную модель временного ряда.

3. Постройте мультипликативную модель временного ряда.

4. Сравните модели по средней ошибке аппроксимации.

5. Выполните прогноз показателя на следующие 4 периода времени по лучшей модели.

Пример выполнения задания

Имеются поквартальные условные данные об объемах потребления электроэнергии жителями региона.

Номер квартала	Потребление электроэнергии жителями региона, млн. кВт×ч	Номер квартала	Товарооборот % к предыдущему периоду
	6,0		8,0
	4,4		5,6
	5,0		6,4
	9,0		11,0
	7,2		9,0
	4,8		6,6
	6,0		7,0
	10,0		10,8

Решение

1. Построим график данного временного ряда. Анализ графика позволяет сделать вывод о наличии в изучаемом временном ряде, во-первых, линейной тенденции, во-вторых, сезонных колебаний периодичностью в четыре квартала (m=4).

Рис. 3.1

Построение аддитивной модели

2.Проведем выравнивание исходных уровней ряда методом скользящей средней с длиной интервала сглаживания, равной 4 по формуле

Для ряда с периодом 12 формула примет вид

№ квартала, t	Потребление электроэнергии, y(t)	Скользящая средняя за четыре квартала
	6,0
	4,4
	5,0	6,25
	9,0	6,45
	7,2	6,625
	4,8	6,875
	6,0	7,1
	10,0	7,3
	8,0	7,45
	5,6	7,625
	6,4	7,875
	11,0	8,125
	9,0	8,325
	6,6	8,375
	7,0
	10,8

3. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и скользящими средними.

№ квартала, t	Потребление электроэнергии, y(t)	Скользящая средняя за четыре квартала	оценки сезонной компоненты

	4,4
		6,25	-1,25
		6,45	2,55
	7,2	6,625	0,575
	4,8	6,875	-2,075
		7,1	-1,1
		7,3	2,7
		7,45	0,55
	5,6	7,625	-2,025
	6,4	7,875	-1,475
		8,125	2,875
		8,325	0,675
	6,6	8,375	-1,775

	10,8

4. Корректировка сезонной компоненты. Аддитивная сезонная компонента должна удовлетворять следующим условиям:

1. Являться периодической функцией с периодом m=4, т.е.

- равенство сезонных компонент в 1 квартале;

- равенство сезонных компонент во 2 квартале;

- равенство сезонных компонент в 3 квартале;

- равенство сезонных компонент в 4 квартале.

Для выполнения этих условий найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты S.

Расчет значений сезонной компоненты в аддитивной модели

Показатели	Год	№ квартала, I
I	II	III	IV
		–	–	–1,250	2,550
		0,575	–2,075	–1,100	2,700
		0,550	–2,025	–1,475	2,875
		0,675	–1,775	–	–
Средняя оценка сезонной,		0,600	–1,958	–1,275	2,708
Скорректированная сезонная компонента,		0,581	–1,977	–1,294	2,690

Для данной модели имеем:

Определим корректирующий коэффициент:

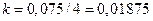Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом k:

Проверим условие равенства нулю суммы значений сезонной компоненты:

Таким образом, получены следующие значения сезонной компоненты:

I квартал:	;
II квартал:	;
III квартал:	;
IV квартал:	.

Занесем полученные значения в таблицу для соответствующих кварталов каждого года.

№ квартала, t	Потребление электроэнергии, y(t)	Скользящая средняя за четыре квартала	оценки сезонной компоненты	Скорректированная сезоная компонента
				0,58125
	4,4			-1,9771
		6,25	-1,25	-1,2938
		6,45	2,55	2,68958
	7,2	6,625	0,575	0,58125
	4,8	6,875	-2,075	-1,9771
		7,1	-1,1	-1,2938
		7,3	2,7	2,68958
		7,45	0,55	0,58125
	5,6	7,625	-2,025	-1,9771
	6,4	7,875	-1,475	-1,2938
		8,125	2,875	2,68958
		8,325	0,675	0,58125
	6,6	8,375	-1,775	-1,9771
				-1,2938
	10,8			2,68958

5. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины Y–S. Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.

№ квартала, t	Потребление электроэнергии, y(t)	Скользящая средняя за четыре квартала	оценки сезонной компоненты	Скорректированная сезоная компонента
				0,58125	5,41875
	4,4			-1,9771	6,37708333
		6,25	-1,25	-1,2938	6,29375
		6,45	2,55	2,68958	6,31041667
	7,2	6,625	0,575	0,58125	6,61875
	4,8	6,875	-2,075	-1,9771	6,77708333
		7,1	-1,1	-1,2938	7,29375
		7,3	2,7	2,68958	7,31041667
		7,45	0,55	0,58125	7,41875
	5,6	7,625	-2,025	-1,9771	7,57708333
	6,4	7,875	-1,475	-1,2938	7,69375
		8,125	2,875	2,68958	8,31041667
		8,325	0,675	0,58125	8,41875
	6,6	8,375	-1,775	-1,9771	8,57708333
				-1,2938	8,29375
	10,8			2,68958	8,11041667

6. Определим трендовую компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда с помощью линейного тренда. Результаты аналитического выравнивания следующие:

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,956541
R-квадрат	0,914971
Нормированный R-квадрат	0,908897
Стандартная ошибка	0,280061
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		11,81602	11,81602	150,6491	7E-09
Остаток		1,098077	0,078434
Итого		12,9141

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	5,715417	0,146865	38,91609	1,14E-15	5,400422	6,030411
t	0,186422	0,015188	12,27392	7E-09	0,153846	0,218998

Таким образом, имеем следующий линейный тренд:

Подставляя в это уравнение значения t =1,…, 16, найдем уровни T для каждого момента времени.

№ квартала, t	Потребление электроэнергии, y(t)	Скользящая средняя за четыре квартала	оценки сезонной компоненты	Скорректированная сезоная компонента
				0,58125	5,4187	5,90184
	4,4			-1,9771	6,3770	6,08826
		6,25	-1,25	-1,2938	6,2937	6,27468
		6,45	2,55	2,68958	6,3104	6,4611
	7,2	6,625	0,575	0,58125	6,6187	6,64752
	4,8	6,875	-2,075	-1,9771	6,7770	6,83395
		7,1	-1,1	-1,2938	7,2937	7,02037
		7,3	2,7	2,68958	7,3104	7,20679
		7,45	0,55	0,58125	7,4187	7,39321
	5,6	7,625	-2,025	-1,9771	7,5770	7,57963
	6,4	7,875	-1,475	-1,2938	7,6937	7,76605
		8,125	2,875	2,68958	8,3104	7,95248
		8,325	0,675	0,58125	8,4187	8,1389
	6,6	8,375	-1,775	-1,9771	8,5770	8,32532
				-1,2938	8,2937	8,51174
	10,8			2,68958	8,1104	8,69816

7. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих кварталов.

№ квартала, t	Потребление электроэнергии, y(t)		T+S
		5,90184	6,48309
	4,4	6,08826	4,11118
		6,27468	4,98093
		6,4611	9,15069
	7,2	6,64752	7,22877
	4,8	6,83395	4,85686
		7,02037	5,72662
		7,20679	9,89637
		7,39321	7,97446
	5,6	7,57963	5,60255
	6,4	7,76605	6,4723
		7,95248	10,6421
		8,1389	8,72015
	6,6	8,32532	6,34824
		8,51174	7,21799
	10,8	8,69816	11,3877

Графически значения (T+S) представлены на рисунке

Рис. 3.2

8.Вычислим абсолютные ошибки по формуле

и относительные ошибки по формуле

№ квартала, t	Потребление электроэнергии, y(t)	T+S		А
		6,48309	-0,4831	8,05%
	4,4	4,11118	0,28882	6,56%
		4,98093	0,01907	0,38%
		9,15069	-0,1507	1,67%
	7,2	7,22877	-0,0288	0,40%
	4,8	4,85686	-0,0569	1,18%
		5,72662	0,27338	4,56%
		9,89637	0,10363	1,04%
		7,97446	0,02554	0,32%
	5,6	5,60255	-0,0025	0,05%
	6,4	6,4723	-0,0723	1,13%
		10,6421	0,35794	3,25%
		8,72015	0,27985	3,11%
	6,6	6,34824	0,25176	3,81%
		7,21799	-0,218	3,11%
	10,8	11,3877	-0,5877	5,44%

Вычислим среднюю ошибку аппроксимации, вычислив среднее значение по столбцу А.

Она составит 2,75%.

12	Поделиться:

Воспользуйтесь поиском по сайту: