 |
Построение мультипликативной модели
|
|
|
|
9. Методика построения мультипликативной модели на первом этапе полностью совпадает с методикой построения аддитивной модели.
Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на скользящие средние.
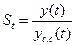
| № квартала, t | Потребление электроэнергии, y(t) | Скользящая средняя за четыре квартала 
| оценки сезонной компоненты
|
| 4,4 | |||
| 6,25 | 0,8 | ||
| 6,45 | 1,39535 | ||
| 7,2 | 6,625 | 1,08679 | |
| 4,8 | 6,875 | 0,69818 | |
| 7,1 | 0,84507 | ||
| 7,3 | 1,36986 | ||
| 7,45 | 1,07383 | ||
| 5,6 | 7,625 | 0,73443 | |
| 6,4 | 7,875 | 0,8127 | |
| 8,125 | 1,35385 | ||
| 8,325 | 1,08108 | ||
| 6,6 | 8,375 | 0,78806 | |
| 10,8 |
10. Корректировка сезонной компоненты. Мультипликативная сезонная компонента должна удовлетворять следующим условиям:
1. Являться периодической функцией с периодом m=4, т.е.
- равенство сезонных компонент в 1 квартале;
- равенство сезонных компонент во 2 квартале;
- равенство сезонных компонент в 3 квартале;
- равенство сезонных компонент в 4 квартале.
2. 
.
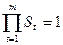Для выполнения этих условий найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты S.
Расчет значений сезонной компоненты в мультипликативной модели
| Показатели | Год | № квартала, I | |||
| I | II | III | IV | ||
| – | – | 0,8000 | 1,3953 | ||
| 1,0868 | 0,6982 | 0,8451 | 1,3699 | ||
| 1,0738 | 0,7344 | 0,8127 | 1,3538 | ||
| 1,0811 | 0,7881 | – | – | ||
Средняя оценка сезонной компоненты для, 
| 1,0806 | 0,7402 | 0,8193 | 1,3730 | |
Скорректированная сезонная компонента, 
| 1,10949127 | 0,76004 | 0,84119 | 1,40977272 |
Для данной модели имеем:
.
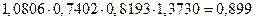Определим корректирующий коэффициент:
.
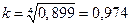Рассчитаем скорректированные значения сезонной, умножив ее средние оценки на корректирующий коэффициент k:
|
|
|
.
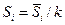Проверим условие равенства единице произведений значений сезонной компоненты:
.
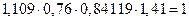Таким образом, получены следующие значения сезонной компоненты:
| I квартал: |  ;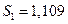
|
| II квартал: |  ;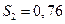
|
| III квартал: |  ;
|
| IV квартал: |  .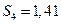
|
Занесем полученные значения в таблицу для соответствующих кварталов каждого года.
11. Исключим влияние сезонной компоненты, разделив каждый уровень исходного временного ряда на ее значение Y/S. Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
| № квартала, t | Потребление электроэнергии, y(t) | Скользящая средняя за четыре квартала
| оценки сезонной компоненты
| Скорректированная сезоная компонента
| 
|
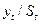
| 1,10949 | 5,40788394 | ||||
| 4,4 | 0,76004 | 5,78919123 | |||
| 6,25 | 0,8 | 0,84119 | 5,94398597 | ||
| 6,45 | 1,39535 | 1,40977 | 6,38400776 | ||
| 7,2 | 6,625 | 1,08679 | 1,10949 | 6,48946073 | |
| 4,8 | 6,875 | 0,69818 | 0,76004 | 6,31548134 | |
| 7,1 | 0,84507 | 0,84119 | 7,13278317 | ||
| 7,3 | 1,36986 | 1,40977 | 7,09334196 | ||
| 7,45 | 1,07383 | 1,10949 | 7,21051193 | ||
| 5,6 | 7,625 | 0,73443 | 0,76004 | 7,36806157 | |
| 6,4 | 7,875 | 0,8127 | 0,84119 | 7,60830204 | |
| 8,125 | 1,35385 | 1,40977 | 7,80267615 | ||
| 8,325 | 1,08108 | 1,10949 | 8,11182592 | ||
| 6,6 | 8,375 | 0,78806 | 0,76004 | 8,68378685 | |
| 0,84119 | 8,32158036 | ||||
| 10,8 | 1,40977 | 7,66080931 |
12. Определим трендовую компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда 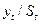с помощью линейного тренда. Результаты аналитического выравнивания следующие:
| ВЫВОД ИТОГОВ | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,948009 | |||||
| R-квадрат | 0,898721 | |||||
| Нормированный R-квадрат | 0,891487 | |||||
| Стандартная ошибка | 0,313552 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 12,21379 | 12,21379 | 124,2317 | 2,4E-08 | ||
| Остаток | 1,376405 | 0,098315 | ||||
| Итого | 13,5902 | |||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 5,4716 | 0,164428 | 33,27718 | 9,96E-15 | 5,119033 | 5,82436 |
| Переменная X 1 | 0,1895 | 0,017005 | 11,14593 | 2,4E-08 | 0,153062 | 0,226005 |
|
|
|
Таким образом, имеем следующий линейный тренд:
.
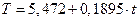Подставляя в это уравнение значения t =1,…, 16, найдем уровни T для каждого момента времени.
| № квартала, t | Потребление электроэнергии, y(t) | Скользящая средняя за четыре квартала
| оценки сезонной компоненты
| Скорректированная сезоная компонента
|
| 
|
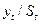
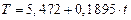
| 1,10949 | 5,4078 | 5,66123 | ||||
| 4,4 | 0,76004 | 5,7891 | 5,85076 | |||
| 6,25 | 0,8 | 0,84119 | 5,9439 | 6,0403 | ||
| 6,45 | 1,39535 | 1,40977 | 6,3840 | 6,22983 | ||
| 7,2 | 6,625 | 1,08679 | 1,10949 | 6,4894 | 6,41936 | |
| 4,8 | 6,875 | 0,69818 | 0,76004 | 6,3154 | 6,6089 | |
| 7,1 | 0,84507 | 0,84119 | 7,1327 | 6,79843 | ||
| 7,3 | 1,36986 | 1,40977 | 7,0933 | 6,98796 | ||
| 7,45 | 1,07383 | 1,10949 | 7,2105 | 7,1775 | ||
| 5,6 | 7,625 | 0,73443 | 0,76004 | 7,3680 | 7,36703 | |
| 6,4 | 7,875 | 0,8127 | 0,84119 | 7,6083 | 7,55656 | |
| 8,125 | 1,35385 | 1,40977 | 7,8026 | 7,7461 | ||
| 8,325 | 1,08108 | 1,10949 | 8,1118 | 7,93563 | ||
| 6,6 | 8,375 | 0,78806 | 0,76004 | 8,6837 | 8,12516 | |
| 0,84119 | 8,3215 | 8,3147 | ||||
| 10,8 | 1,40977 | 7,6608 | 8,50423 |
13. Найдем значения уровней ряда, полученные по мультипликативной модели. Для этого умножим уровни T на значения сезонной компоненты для соответствующих кварталов.
| № квартала, t | Потребление электроэнергии, y(t) |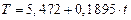
| T*S |
| 5,90184 | 6,281 | ||
| 4,4 | 6,08826 | 4,447 | |
| 6,27468 | 5,081 | ||
| 6,4611 | 8,783 | ||
| 7,2 | 6,64752 | 7,122 | |
| 4,8 | 6,83395 | 5,023 | |
| 7,02037 | 5,719 | ||
| 7,20679 | 9,851 | ||
| 7,39321 | 7,963 | ||
| 5,6 | 7,57963 | 5,599 | |
| 6,4 | 7,76605 | 6,356 | |
| 7,95248 | 10,920 | ||
| 8,1389 | 8,805 | ||
| 6,6 | 8,32532 | 6,175 | |
| 8,51174 | 6,994 | ||
| 10,8 | 8,69816 | 11,989 |
Графически значения (T×S) представлены на рисунке
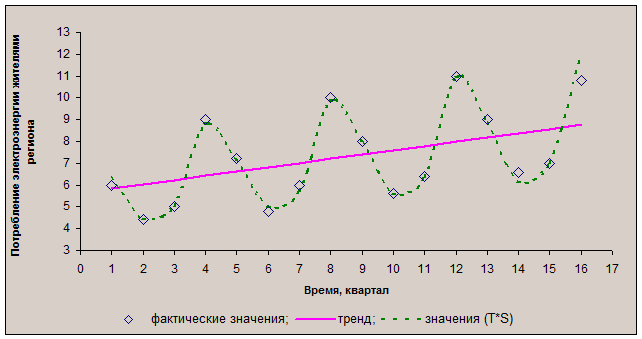
14. Вычислим абсолютные ошибки по формуле
и относительные ошибки по формуле
| № квартала, t | Потребление электроэнергии, y(t) | T*S |
| А |
| 6,281 | -0,2811 | 4,68% | ||
| 4,4 | 4,447 | -0,0468 | 1,06% | |
| 5,081 | -0,081 | 1,62% | ||
| 8,783 | 0,21736 | 2,42% | ||
| 7,2 | 7,122 | 0,07777 | 1,08% | |
| 4,8 | 5,023 | -0,223 | 4,65% | |
| 5,719 | 0,28125 | 4,69% | ||
| 9,851 | 0,14856 | 1,49% | ||
| 7,963 | 0,03663 | 0,46% | ||
| 5,6 | 5,599 | 0,00078 | 0,01% | |
| 6,4 | 6,356 | 0,04352 | 0,68% | |
| 10,920 | 0,07976 | 0,73% | ||
| 8,805 | 0,19549 | 2,17% | ||
| 6,6 | 6,175 | 0,42457 | 6,43% | |
| 6,994 | 0,00579 | 0,08% | ||
| 10,8 | 11,989 | -1,189 | 11,01% |
Вычислим среднюю ошибку аппроксимации, вычислив среднее значение по столбцу А. Она составит 2,70%.
|
|
|
Таким образом, мультипликативная модель дала более высокое качество прогноза, чем аддитивная.
|
|
|
12 |
