 |
Оформление результатов выполнения задания
|
|
|
|
1 Титульный лист
2 Номер и название практического занятия.
3 Цель занятия.
4 Задание.
5 Объект исследования, таблица экспериментальных данных, корреляционное поле y(x).
6 Формулы с пояснениями для расчета корреляционного отношения Пирсона, распечатка результатов расчета в среде MathCAD.
7 Выводы о виде зависимости.
Практическое занятие № 7. Проверка адекватности уравнений регрессии объекту исследования
Цель работы: овладетьнавыками определения адекватности уравнений регрессии объекту исследования с помощью критерия Фишера
Задание
1 По результатам экспериментальных данных объекта исследования определить количество серий опытов и количество параллельных опытов в каждой серии.
2 Выявить число переменных (факторов) x, влияющих на выходную координату y, определить вид м атематической модели.
3 Определить расчетное значение критерия Фишера.
4 Проверить полученную математическую модель на адекватность.
Объект исследования и результаты экспериментальных данных
Для описания объекта исследования проведена серия параллельных опытов. Экспериментальные данные представлены в таблице 2.1.
Таблица 2.1 – Результаты параллельных опытов
| № серии опытов, i | Вход xi | Выход yij в параллельных опытах j | 
| 
| ||
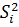
| 3,8 | 4,0 | |||||
Для описания одномерного объекта исследования получена математическая модель в виде уравнения регрессии:
Y=4+6х. (2.1)
Указания по выполнению задания
2.2.1.Назначение экспериментальных исследований. Основная цель экспериментальных исследований – построение математической модели исследуемого в эксперименте объекта. Для достоверности полученных результатов проводят серию параллельных опытов.
|
|
|
Параллельные опыты – опыты, проведенные несколько раз при одних и тех же значениях входа. Результаты опытов заносятся в таблицу 2.2, где k –количество параллельных опытов (обычно k = 2…4); N –количество серий параллельных опытов.
Таблица 2.2 – Результаты параллельных опытов, результаты расчетов
| № серии опытов, i | Вход xi | Выход yij в параллельных опытах j |
|
| |||
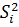
| x1 | y11 | y12 | … | y1k | |||
| x2 | Y21 | Y22 | … | y2k | |||
| … | … | … | … | … | … | ||
| i | xi | … | … | yij | yik … |
| … | … | … | … | … | … | ||
| N | xN | yN1 | yN2 | … | yNk | ||
| Sвоспр2=; Sад2=; fвоспр =; fад =; | |||||||
| FР =; FT =; |
2.2.2 Обработка экспериментальных данных. Для каждой серии параллельных опытов вычисляют среднее арифметическое
значение:
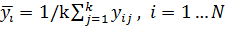(2.2)
Затем для каждой серии параллельных опытов вычисляют оценку дисперсии:
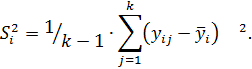(2.3)
Оценка воспроизводимости определяется выражением:
. (2.4)
2.2.3 Проверка математической модели на адекватность. Под адекватностью понимают способность построенной математической модели соответствовать результатам эксперимента с заданной сте-
пенью точности. Эту проверку осуществляют с помощью критерия Фишера:
, (2.5)
где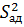 
– оценка дисперсии адекватности,
, (2.6)
где Yi – значение выхода, рассчитанное по модели, по известному входу хi.,
Для одномерного объекта исследования линейная модель имеет вид:
Yi=а0+а1хi.. (2.7)
С дисперсией адекватности связывают коэффициенты:
fвоспр=N(k-1), (2.8)
fад=N-(n+1),
где n – число входов х (n=1).
По таблице 2.3 с вероятностью, равной Р=0,95 определяют табличное значение критерия Фишера FT.
Таблица 2.3 - Значение критерия Фишера FT (P=0,95)
| fвоспр | fад | |||
| 161, | 199,5 | 215,7 | 224,6 | |
| 518,51 | 19,00 | 19,16 | 19,25 | |
| 10,13 | 9,55 | 9,28 | 9,12 | |
| 7,71 | 6,94 | 6,59 | 6,39 | |
| 6,61 | 5,79 | 5,41 | 5,19 | |
| 5,99 | 5,14 | 4,76 | 4,53 | |
| 5,59 | 4,74 | 4,35 | 4,12 | |
| 5,32 | 4,46 | 4,07 | 3,84 | |
| 5,12 | 4,24 | 3,86 | 3,63 | |
| 4,97 | 4,10 | 3,71 | 3,48 | |
| 4,84 | 3,98 | 3,59 | 3,36 | |
| 4,75 | 3,89 | 3,49 | 3,26 |
Модель считается адекватной объекту исследования, если выполняется условие:
|
|
|
FР ≤FT. (2.9)
Если полученная модель не адекватна, в качестве модели выбирают уравнение регрессии в виде степенного полинома более высокого порядка и расчеты повторяют
|
|
|
