 |
Оформление результатов выполнения задания
|
|
|
|
1 Номер и название практического занятия.
2. Задание.
3. Таблица экспериментальных данных пассивного эксперимента.
4. Вид статической модели в общем виде, с пояснениями.
5. Выбранный вид статической математической модели.
5. Матрица наблюдений.
6 Система уравнений для определения коэффициентов модели.
7 Таблица расчетных значений.
8. Графики экспериментальных и расчетных значений.
9. Определение адекватности статической модели исследуемого объекта.
4 Практическое занятие № 8. Проведение обработки результатов эксперимента по кривым разгона
Цель работы: овладетьнавыками обработки экспериментальных данных для получения модели динамики объекта, аппроксимирующей поведение реального объекта.
Задание
1 По экспериментальным данным, указанным преподавателем, построить кривую разгона в относительных единицах.
2 По виду кривой разгона определить характер объекта.
3 Выбрать вид моделей динамики объекта управления.
4 Определить предполагаемые коэффициенты математических моделей с характеристическими уравнениями первого и более высокого порядков для одного и того же объекта.
5 Проверить полученные модели на адекватность.
6 Проверить модель на адекватность.
Объекты управления и результаты экспериментальных исследований
В таблице 4.1, таблице 4.2 приведены экспериментальные данные кривых разгона объектов, полученные при перестановке регулирующего органа на 20% (ступенчатое входное воздействие составляет в относительных единицах А=0.2).
1 Объект управления - топливный бак, в котором контролируется уровень топлива Н, м для обеспечения постоянной подачи в двигатель внутреннего сгорания.
|
|
|
Таблица 4.1- Экспериментальные данные кривой разгона
| Время, с | ||||||
| Уровень Н, м | 0,02 | 0,08 | 0,15 | 0,20 | 0,35 | 0,40 |
| Время, с | ||||||
| Уровень Н, м | 0,45 | 0,50 | 0,55 | 0,58 | 0,60 | 0,60 |
2. Объект управления – расширительный бачок, в котором контролируется температура охлаждающей жидкости Q,0С.
Таблица 4.2- Экспериментальные данные кривой разгона
| Время t, с | ||||||
| Температура Q,0С. | 80,0 | 80,1 | 80,1 | 80,2 | 80,3 | 80,8 |
| Время t, с | ||||||
| Температура Q,0С. | 81,1 | 81,5 | 83,0 | 84,0 | 85,5 | 85,5 |
Методические рекомендации
.
Обработка экспериментальных данных при идентификации зависит от степени искажения данных и от принятых моделей, аппроксимирующих поведение реального объекта.
Возможны различные типы кривых разгона. Соответственно используются и различные модели реальных объектов.
4.2.1 Математическая модель динамики объекта: в виде передаточной функции
(4.1)
|
; (4.2)
где А - ступенчатое входное воздействие, y(0), y(tN) - начальное и установившееся значение выходной переменной.
Т0, t0, k0 определяются графо-аналитическим методом по кривой разгона, представленной на рисунке 4.1.
 |
Рисунок 5.1 –Экспериментальная кривая разгона объекта управления в относительных единицах
Экспериментальные значения для построения кривой разгона в относительных единицах определяются выражением: 
4.2.2 Математическая модель динамики объекта в виде передаточной функцией с характеристическим уравнением второго порядка:
(4.3)
Используя метод площадей трапеции и известную теорему операционного исчисления о предельном переходе, получим:
(4.4)
(4.5)
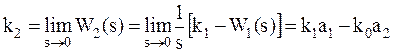. (4.6)
Неизвестные значения коэффициентов k0, k1, k2 находим последовательным интегрированием реакции h(t) согласно соотношениям:
|
|
|
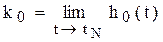(4.7)
(4.8)
(4.9)
Последовательность нахождения коэффициентов a1, a2 передаточной функции по методу площадей трапеций:
1) По исходным данным строят график переходной функции h0(t)=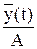 
;
2) Численным методом находят площадь под кривой k0-h0(t) или функцию h1(t), значения которой запоминаются;
3) Определяют значение h1(t)=k1 и строят график h1(t);
4) Находятм площадь под кривой k1-h1(t) при t=tN или значение функции h2(t)=k2;
Интегралы (8) и (9) находятся приближенно по методу трапеций:
(4.10)
где N=t/Dt — число точек,
Dt — шаг измерений;
.
4.2.3 Математическая модель динамики объекта в виде передаточной функцией с характеристическим уравнением более высокого порядка:
(4.11)
Коэффициенты передаточной функции аi и b находят по методу площадей Симою. Для этого вначале рассчитывают площади Si, определяемые по кривой разгона:
(4.12)
где 
(4.13)
Рассчитывается Sgо по одной из формул приближенного вычисления определенного интеграла, например метод «трапеций»:
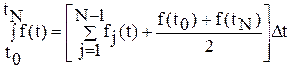(4.14)
где N - число точек, 
, 
- шаг интегрирования.
По мере расчета Si определяют значение 
.
Если это отношение станет меньше заданного значения D, вычисления Si прекращают, полагая порядок знаменателя передаточной функции (5) равным 
, тогда:
b=0; aj = Sj; j = 1..i-1. (4.15)
Если Si станет меньше нуля, то независимо от значения 
вычисления прекращают и полагают порядок знаменателя равным 
.
aj = Sj-b1Sj-1, j=1..i-1, 
. (4.16)
Если b<D, расчеты ведут по (15) и b1 не учитывают.
4.2.4 Для построения расчетных значений модели (4.1), (4.3), (4.11) - воспользоваться пакетом прикладных программ MATLAB, MathCAD
4.2.5 Аппроксимация признается удовлетворительной, если максимальное расхождение между экспериментальными и расчетными данными кривой разгона не превышает 0.1. Адекватность можно проверить по среднеквадратичному отклонению:
, (12)
где: yi – экспериментальные значения;Yi – вычисленные значения.
Содержание отчета
1 Цель работы
2 Задание
3 Объект управления и результаты экспериментальных исследований
4 Таблица экспериментальных и расчетных данных по кривым разгона.
5 Алгоритм расчета моделей динамики объекта по методу площадей трапеций. методу площадей Симою с распечаткой результатов в среде MathCAD, MATLAB.
|
|
|
6 Графики кривых разгона (экспериментальной, расчетных по трем методам) с построениями для определения динамических параметров объекта управления.
7 Выводы по адекватности моделей в результате идентификации.
Список литературы
1 Олехнович, Г. И. Интеллектуальная собственность и проблемы ее коммерциализации / Г. И. Олехнович. - 2-е изд., перераб. и доп. – Минск: Амалфея, 2005. – 128 с.
2 Сергеев, А. П. Патентное право: учеб. пособие/ А. П. Сергеев. - М.: БЕК, 1994. - 202 с.
3 Методика и техника инженерного эксперимента: учеб. пособие / Под ред. В. П. Березиенко, В. Г. Лупачева. - Могилев: Белорус.-Рос. ун-т, 2008.- 278 с.
4 Чернышов Е. А. Основы инженерного творчества в дипломном проектировании и магистерских диссертациях: учеб. пособие для вузов / Е. А. Чернышов. - М.: Высш. шк., 2008. – 254 с.
|
|
|
