Пространство элементарных событий

ЗАДАЧИ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

1.1.1. Монету подбрасывают дважды. Описать пространство элементарных событий. Описать события: А - по крайней мере, один раз появится герб; В - при втором подбрасывании появится герб.

1.1.2. Подбрасывают монету, а после этого подбрасывают игральную кость. Описать пространство элементарных событий.

1.1.3. Подбрасывают монету до тех, пока не выпадет герб. Описать пространство элементарных событий.

1.1.4. Пусть эксперимент состоит в измерении двух величин, которые принимают значения из отрезка [0,1].Описать пространство элементарных событий.

1.1.5. Построить множество элементарных событий в эксперименте, который состоит в выборе из урны, содержащей m белых и n черных шаров, k шаров k<n+m. Каково число элементарных событий?

Решить эту задачу, если шары вынимаются последовательно один за одним.

1.1.6. Из цифр 1,2,3,4,5 сначала выбирают одну; потом из четырех оставшихся цифр выбирают другую. Описать пространство элементарных событий. Считая, что все элементарные события равновозможны, вычислить вероятность следующих событий: а) первый раз выбрана нечетная цифр; б) второй раз выбрана нечетная цифра; в) и первый, и второй раз выбрана нечетная цифра.

1.1.7. Монету подбрасывают до тех пор, пока она не выпадает дважды подряд одной стороной. Описать пространство элементарных событий. Каждому элементарному событию, которое требует n подбрасываний, принимаем вероятность Вычислить вероятность таких событий: а) эксперимент окончится до шестого подбрасывания; б) будет совершенно четное число подбрасываний; в) эксперимент продлится бесконечно долго.

1.1.8. Три игрока a,b,c проводят шахматный турнир по следующей схеме: в первом туре играют a, и b, игрок c свободен; во втором туре играет победитель первого тура и c, а игрок, проигравший в первом туре, свободен. Турнир продолжается до тех пор, пока один из игроков не выиграет подряд две партии (он и объявляет победителем турнира). Ничейных партий нет. Описать пространство элементарных событий. Каждому элементарному событию, которое состоит из k партий, припишем вероятность . Вычислить вероятности таких событий: а) победителем будет а; б) победителем будет b; в) победитель будет с; г) победитель не выяснится до n - го тура; д) турнир никогда не окончится.

1.1.9. Два различных шара кладут в две урны. Описать пространство элементарных событий. Считая, что все элементарные события равновозможны, вычислить вероятность того, что есть урна, в которой нет ни одного шара.

1.1.10. Два одинаковых шара кладут в две урны. Описать пространство элементарных событий. Считая, что все элементарные события равновозможны, вычислить вероятность того, что есть урна, не содержащая ни одного шара.

1.1.11. Мишень состоит из 10 кругов, ограниченных концентрическими окружностями с радиусами причем . Событие состоит в попадании в круг радиуса . Что означает события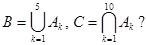

1.1.12. Указать события, противоположные таким событиям: а) А - появление герба при двух подбрасываниях монеты; б) B - три попадания при трех выстрелах; в) С - по крайней мере, одно попадание при трех выстрелах.

1.1.13. Сделано три выстрела по мишени. Пусть - событие, состоящее в том, что при i - м выстреле есть попадание (i=1,2,3). Выразить через события А, такие события: а) А - произошло три попадания; б) В - не было ни одного попадания; в) только одно попадание; г) не менее двух попаданий.

1.1.14. Бросают две игральные кости. Пусть А-событие, которое состоит в том, что сумма очков нечетна; В - выпадает, по крайне мере, одна единица. Описать события А∩В, А 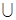В, А∩В. Найти их вероятности, считая, что все элементарные события равновозможны.

1.1.15. Пусть А, В, С - три случайных события. Записать события, которые состоят в том, что из А, В, С:

а) произошло только событие А;

б) произошли А и В и не произошло С;

в) произошли все три события;

г) произошло, по крайне мере, одно событие;

д) произошло одно и только одно событие;

е) произошло не более двух событий;

ж) не произошло ни одно событие.

 

Комбинаторика

1.2.1. Из города А в город В ведет n дорог, из города В в город С – m дорог. Сколькими способами можно совершить путешествие по маршу руту А-В-С?

1.2.2. На вершину горы ведет 7 дорог. Сколькими способами турист может взобраться на гору и спуститься с нее? Дать ответ на тот же вопрос, если подьем и спуск происходит разными путями.

1.2. 3 В розыгрыше первенства страны по футболу принимают участие 17 команд. Сколькими способами могу быть распределены золотая, серебренная и бронзовая медали?

1.2.4 Сколько трехзначных чисел можно написать с помощью цифр 0,1,2,3,4?

1.2.5 Сколько трехзначных чисел можно написать с помощью цифр 0,1,2,3,4 если каждую из цифр использовать не больше одного раза?

1.2.6. Сколькими способами 7 лиц могут разместиться в очереди к кассе?

1.2.7. В классе изучают 10 предметов. В понедельник 6 уроков, причем все уроки разные. Сколькими способами можно составить расписание на понедельник?

1.2.8. Сколько есть пятизначных чисел, которые делятся на 5?

1.2.9. В турнире принимает участие n шахматистов. Сколько партий будет сыгранно в шахматном турнире, если каждые 2 участника встретятся один раз?

1.2.10. Сколько диагоналей можно провести в выпуклом n – угольнике?

1.2.11. Сколькими способами можно расставить на шахматной доске размерами n* n две разноцветные ладьи так, чтобы они не били друг друга?

1.2.12. Автомобильный номер состоит из двух букв и четырех цифр. Сколько различных номеров можно составить, используя 32 буквы русского алфавита?

1.2.13. Если повернуть лист бумаги на 180 градусов, то цифры 0,1,8 не изменяются, 6 и 9 переходят друг в друга, а другие цифры теряют смысл. Сколько существуют семизначных чисел, величина которых не изменится при повороте листа бумаги на 180 гадусов?

1.2.14. В розыгрышепервенства страны по футболу в высшей лиге класса А участвует 16 команд. Команды, которые занимают первое, второе и третье места, награждаются соответственно золотой, серебрянной и бронзовой медалями, а команды, которые окажутся на последних двух местах, покинут высшую лигу. Сколько различных результатов первенства может быть?

1.2.15. Пасажир оставил вещи в автоматической камере хранения, а когда пришел забирать вещи, то оказался, что забыл номер. Пасажир помнит лишь, что в номере были числа 23 и 37. Чтобы открыть камеру нужно правильно набрать пятизначный номер. Какое наибоьшее количество номеров нужно перебрать, чтобв открыть камеру

1.2.16. Сколькими способами можно из 9 лиц выбрать комиссию, которая состоит из4 лиц?

1.2.17. Сколькими способами можно рассадить четырех учеников на 25 местах?

1.2.18. Сколькими способами можно упорядочить множество 1,2,..., n так, чтобы числа 1,2,3 стояли рядом и в порядке возрастания?

1.2.19. Из 100 студентов английский язык знают 28 студентов, немецкий –30, французский- 42, английский и немецкий –8, английский и французский-10, немецкий и французский-5, все 3 языка знают 3 студента. Сколько студентов не знают ни одного из трех языков?

 

12	Поделиться:

Воспользуйтесь поиском по сайту: