 |
Расчетно-графическое задание №1
|
|
|
|
Определение реакций опор составной конструкции (система сочлененных тел)
Найти реакции опор и давление в промежуточном шарнире составной конструкции. Схемы конструкций представлены на рисунках, размеры в (м), нагрузка в табл.1
Пример выполнения задания:
Дано: схема конструкции (рис. 1); Р1 = 10 кн; Р2 = 12 кн; М =25 кнм; q = 2 кн/м; a = 60º.
Определить реакции опор и давление в промежуточном шарнире.
Решение:
Сначала рассмотрим систему уравновешивающихся сил, приложенных ко всей конструкции (рис.2), что позволит определить вертикальные составляющие реакции опор А и В. Для упрощения вычисления момента силы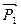 
раскладываем ее на составляющие по осям 
и 
: 
= P 1 cosa = 10 • 0,5 = 5 кн;
= Р 1 sina = 10 • 0,866 = 8,66 кн.
Рис. 1
Рис.2
Уравнения равновесия имеют вид
S Мi А = 0; • 4 + • 3 - Q • 2 - М – P 2 • 5 + Y B • 7= 0, (1)
где Q = L • q = 4 • 2 = 8 кн;
S Yi = 0; - + Y A - P 2 + Y B = 0; (2)
S Xi = 0; Х A + Х B - + Q = 0. (3)
Из уравнения (1)
Y B = 
= 
= 7,86 кн.
Из уравнения (2)
Y A = + Р 2 — Y B = 8,66 + 12 — 7,86 = 12,8 кн.
Уравнение (3), содержащее два неизвестных, не позволяет определить их числовые значения.
Рассмотрим теперь систему уравновешивающихся сил, приложенных к правой части конструкции (рис. 3).
Рис.3
S МiC = 0; - M -P 2 • 2 + X B • 4 = 0; (4)
S Xi = 0; X B + X C = 0; (5)
S Yi = 0; Y C - P 2 + Y B = 0. (6)
Из уравнения (4)
X B =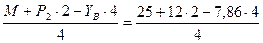 
= 4,39 кн.
Из уравнения (5)
Х С = — Х В = —4,39 кн.
Из уравнения (6)
Y C = P 2 - Y B = 12 — 7,86 = 4,14 кн.
Из уравнения (3)
ХА = — Х В + — Q = —4,39 + 5 — 8 = —7,39 кн.
Для проверки правильности решения задачи убедимся в том, что соблюдается уравнение равновесия для сил, приложенных ко всей конструкции (см. рис. 2):
S MiB = 0; • 4 + • 10 - Q • 2 - Y A • 7 - М + Р 2 • 2 =
= 5 • 4 + 8,66 • 10 — 8 • 2—12, 8 • 7 — 25 + 12 • 2 = 130,6 — 130,6=0.
Результаты расчета сведем в таблицу.
|
|
|
| Силы, кн | |||||
| Х А | Y A | X B | Y B | X C | Y C |
| -7,39 | 12,8 | 4,39 | 7,86 | -4,39 | 4,14 |
Таблица 1
| Номер варианта | Р1 | Р2 | М,кнм | q, кн/м | |||
| кн | |||||||
| 6,0 | — | 25,0 | 0,8 | ||||
| 5,0 | 8,0 | 26,0 | — | ||||
| 8,0 | 10,0 | 33,0 | 1,1 | ||||
| 10,0 | — | 25,0 | 1,3 | ||||
| 12,0 | — | 27,0 | 1,0 | ||||
| 14,0 | 12,0 | — | 0,9 | ||||
| 16,0 | 8,0 | 18,0 | 1,4 | ||||
| 12,0 | 6,0 | 20,0 | 1,0 | ||||
| 14,0 | — | 28,0 | 1,4 | ||||
| 8,0 | — | 26,0 | 0,9 | ||||
| 15,0 | 10,0 | 29,0 | 1,0 | ||||
| 15,0 | 8,0 | 28,0 | 1,5 | ||||
| 7,0 | 6,0 | 15,0 | 1,1 | ||||
| 5,0 | — | 30,0 | 0,9 | ||||
| 6,0 | 10,0 | 24,0 | 1,5 | ||||
| 8,0 | 11,0 | 31,0 | 0,8 | ||||
| 9,0 | 15,0 | 26,0 | 1,1 | ||||
| 7,0 | 16,0 | 27,0 | 0,8 | ||||
| 6,0 | 18,0 | 35,0 | 1,4 | ||||
| 7,0 | 16,0 | 32,0 | 0,8 | ||||
| 8,0 | 17,0 | 30,0 | 1,2 | ||||
| 5,0 | 6,0 | 34,0 | 1,5 | ||||
| 14,0 | 10,0 | 36,0 | 1,2 | ||||
| 10,0 | 13,0 | 28,0 | 1,3 | ||||
| 11,0 | 10,0 | 33,0 | 1,0 | ||||
| 15,0 | 15,0 | 18,0 | 1,4 | ||||
| 11,0 | 14,0 | 36,0 | 1,5 | ||||
| 12,0 | 12,0 | 30,0 | 1,1 | ||||
| 10,0 | 9,0 | 35,0 | 1,3 | ||||
| 9,0 | 10,0 | 29,0 | 1,5 | ||||
Центр тяжести тела.
Центр тяжести – точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил. Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
(2.1)
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 12), то вес 
каждого отрезка 
можно представить в виде произведения:
,
где d – постоянный для всей фигуры вес единицы длины материала.
рис.12 рис.13
После подстановки в формулы (2.1) вместо их значений 
постоянный множитель 
в каждом слагаемом числителя и знаменателя можно вынести за скобки (за знак суммы) и сократить. Таким образом, формулы для определения координат центра тяжести фигуры, составленной из отрезков линий, примут вид:
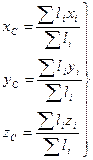(2.2)
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 13), то вес каждой плоскости (поверхности) можно представить так:
|
|
|
,
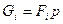где 
– площади каждой поверхности, а 
– вес единицы площади фигуры.
После подстановки этого значения в формулы (2.1) получаем формулы координат центра тяжести фигуры, составленной из площадей:
(2.3)
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 14), то вес каждой части 
, где 
– объем каждой части, а 
– вес единицы объема тела.
После подстановки значений в формулы (2.1) получаем формулы для определения координат центра тяжести тела, составленного из однородных объемов:
(2.4)
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
Если известен радиус дуги 
и центральный угол 
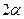, стягиваемый дугой и выраженный в радианах, то положение центра тяжести С (рис. 15, а) относительно центра дуги О определится формулой
. (2.5)
Если же задана хорда (
) дуги, то в формуле (2.5) можно произвести замену
и тогда
. (2.5а)
В частном случае для полуокружности обе формулы примут вид (рис. 184, б)
. (2.5б)
Положение центра тяжести кругового сектора, если задан его радиус (рис. 15, в), определяется при помощи формулы
. (2.6)
Если же задана хорда сектора, то 
. (2.6а)
|
|
рис.14 рис.15
В частном случае для полукруга обе последние формулы примут вид (рис. 15, г)
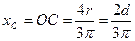. (2.6-б)
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 16).
При решении задач на определение положения центра тяжести любого однородного тела, составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
1) 
выполнить рисунок тела, положение центра тяжести которого нужно определить в масштабе;
2) разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из известных размеров по чертежам;
|
|
|
3) определить длины (площади, объемы) составных частей;
4) выбрать расположение осей координат или оно уже известно;
5) определить координаты центров тяжести составных частей;
6) найденные значения подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
7) по найденным координатам указать на рисунке положение рис.16
8) центра тяжести для всего тела.
|
|
|
