 |
Детерминированный (функциональный) и стохастический (корреляционный) анализ. Основные свойства детерминированного подхода к анализу
|
|
|
|
Создать факторную систему – значит представить изучаемое явление в виде алгебраической суммы, частного или произведения нескольких факторов, что воздействуют на его величину и находятся с ним в функциональной зависимости.
Например, объем валовой продукции промышленного предприятия можно представить в виде произведения двух факторов первого порядка: среднего количества рабочих и среднегодовой выработки продукции одним рабочим за год, которая, в свою очередь, зависит непосредственно от количества отработанных дней одним рабочим в среднем за год и среднедневной выработки продукции рабочим. Последняя также может быть разложена на продолжительность рабочего дня и среднечасовую выработку
Развитие детерминированной факторной системы достигается, как правило, за счет детализации комплексных факторов. Элементные (в нашем примере – количество рабочих, количество отработанных дней, продолжительность рабочего дня) не раскладываются на сомножители, так как по своему содержанию они однородны. С развитием системы количественные факторы постепенно детализируются на менее общие, те в свою очередь еще на менее общие, постепенно приближаясь по своему аналитическому содержанию к элементным (простым).
Таким образом, систематизация факторов позволяет более глубоко изучить взаимосвязь факторов при формировании величины изучаемого показателя, что имеет немаловажное значение на следующих этапах анализа, особенно на этапе моделирования исследуемых показателей.
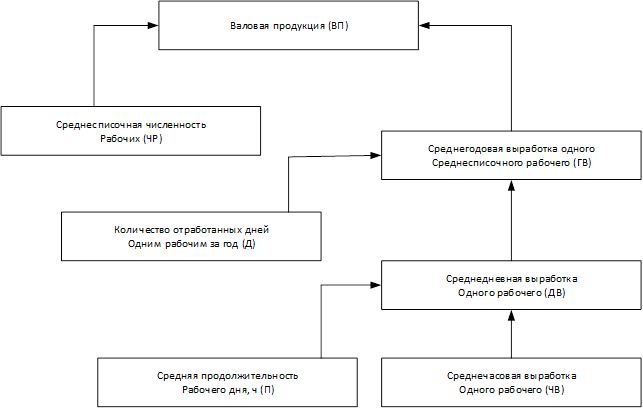
Рисунок 2. Детерминированная факторная система валовой продукции
На практике не все экономические явления можно изучать с помощью четкой функциональной зависимости. Для таких процессов характерно то, что за причиной некоторого явления не всегда наступает следствие. Купив лотерейный билет, не стоит сразу записываться на курсы водителей автомобиля. Такие процессы носят название стохастических (случайных).
|
|
|
Стохастические зависимости отличаются приблизительностью, неопределенностью. Для случайных процессов, так же, как и для детерминированных, проводится факторный анализ оценки влияния различных факторов на результирующий показатель.
Для организации конкретного исследования стохастического процесса приходится регистрировать значительно большие объемы информации. Это связано с тем, что при изучении стохастических зависимостей действует закон больших чисел - чем больший объем информации имеется в распоряжении исследователя, тем с большей точностью получаются результаты такого исследования.
Но главное различие заключается в том, что исследуются вероятностные стохастические зависимости результирующего параметра от влияющих на него факторов. В отличие от детерминированного анализа одному набору факторов могут соответствовать различные значения результирующего показателя, и наоборот, одному значению результирующего фактора - различные наборы факторных переменных.
Исследование стохастических процессов (стохастический анализ) проводится в три этапа:
- оценка существующего положения предприятия;
- анализ взаимозависимостей между различными показателями-факторами и их влияния на результирующий показатель;
- прогнозирование экономического положения предприятия на некоторый промежуток времени, который иногда называется горизонтом планирования.
Факторный стохастический анализ - это общее название целого комплекса методов исследования взаимозависимостей результирующего показателя (или нескольких результирующих показателей) от одного или нескольких независимых факторов.
|
|
|
Формально можно записать:

где Т- тренд, или детерминированная составляющая, С- периодическая (циклическая) и R - случайная составляющие.
В простейшем случае исследуемый процесс представляет собой обыкновенную алгебраическую сумму трех составляющих:

Главное отличие стохастического факторного анализа от других методов исследования в том, что он имеет больше количественный, чем качественный характер.
Основные методики данного типа анализа:
Метод парной корреляции. Широко применяется для выяснения того, насколько между собой связаны различные показатели, которые не связаны между собой явной функцией.
Матричная модель. Схематично отражают тот или иной экономический процесс при помощи абстрагирования. Используется, например, при определении связи между расходами и результатами производственной деятельности.
Метод математического программирования. Главный инструмент решения оптимизационных задач, по результатам которого руководство компании может выбрать самый эффективный путь развития.
Метод изучения операций. Используется при изучении конкретной финансовой проблемы.
Теория игр. По сути, является подразделом предыдущего пункта, однако ее отличительной особенностью является изучение ситуации с разных точек зрения.
|
|
|


